Addition and Subtraction of Fractions

Addition and subtraction of fractions are discussed here with examples.

To add or subtract two or more fractions, proceed as under:

(i) Convert the mixed fractions (if any.) or natural numbers to improper fraction.

(ii) Find the L.C.M of the denominators of the fractions and place the L.C.M below a horizontal bar.

(iii) The L.C.M is then divided by each denominator and the quotient is multiplied to the corresponding numerator. The results obtained are placed above the horizontal bar with proper sign (+) or (-) to obtain a single fraction.

(iv) Reduce the fraction obtained to simplest form and then convert it into mixed form if needed.

In order to add or subtract like fractions, we add or subtract their numerators and retain the common denominator. 

Examples on addition or subtraction with like fractions;

(i) 5/8 + 2/8

= (5 + 2)/8

= 7/8


(ii) 11/5 – 7/15

= (11 – 7)/15

= 4/15


(iii) 16/5 – 3/5 + 2/5 – 9/5

= (16 – 3 + 2 - 9)/5

= (18 – 12)/5

= 6/5


(iv) 4²/₃ + 1/3 – 4¹/₃

= (4 × 3 + 2)/3 + 1/3 – (4× 3 + 1)/3

= 14/3 + 1/3 – 13/3

= (14 + 1 - 13)/3

= (15 - 13)/3

= 2/3

In order to add and subtract unlike fractions, we follow the following steps:

STEP I: Obtain the fractions and their denominators.

STEP II: Find the LCM of the denominators.

STEP III: Convert each of the fraction into an equivalent fraction having its denominator equal to the Least Common Multiple (LCM) obtained in step II.

STEP IV: Add or subtract like fractions obtained in step III.

Examples on addition or subtraction with unlike fractions;

1. Add:

(i) 7/10 + 2/15

(ii) 2²/₃ + 3¹/₂



Solution:

(i) 7/10 + 2/15

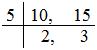
LCM of 10 and 15 is (5 × 2 × 3) = 30.

So, we convert the given fractions into equivalent fractions with denominator 30.

7/10 = (7× 3)/(10 × 3) = 21/30 , and 2/15 = (2 × 2)/(15 × 2) = 4/30

Therefore, 7/10 + 2/15

= 21/30 + 4/30

= (21 + 4)/30

=

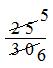
= 5/6


(ii) 2²/₃3 + 3¹/₂

= (2 × 3 + 2)/3 + (3 × 2 + 1)/2

= 8/3 +7/2

= (8× 2)/(3× 2)+ (7× 3)/(2× 3)

[Since least common multiple (LCM) of 3 and 2 is 6; so, convert each fraction to an equivalent fraction with denominator 6]

= 16/6 + 21/6

= (16 + 21)/6

= 37/6



2. Simplify:

(i) 15/16 – 11/12

(ii) 11/15 – 7/20


(i) 15/16 – 11/12

Least common multiple (LCM) of 16 and 12 = (4 × 4 × 3) = 48.

= (15 × 3)/(16 × 3) – (11 × 4)/(12 × 4)

[Converting each fraction to an equivalent fraction with denominator 48]

= 45/48 – 44/48

= (45 – 44)/48

= 1/48


(ii) 11/15 – 7/20

Least common multiple (LCM) of 15 and 12 = 5 × 3 × 4 = 60

= (11 × 4)/(15 × 4) – (7 × 3)/(20 × 3)

[Converting each fraction to an equivalent fraction with denominator 60]

= 44/60 – 21/60

= (44 – 21)/60

= 23/60



3. Simplify: 4⁵/₆ – 2³/₈ + 3⁷/₁₂

Solution:

4⁵/₆ – 2³/₈ + 3⁷/₁₂

= (6 × 4 + 5)/6 – (2 × 8 + 3)/8 + (3 × 12 + 7)/12

= 29/6 – 19/8 + 43/12

= 29/6 – 19/8 + 43/12

= (29 × 4)/(6 × 4) – (19 × 3)/(8 × 3) + (43 × 2)/(12 × 2)

[Since, LCM of 6, 8, 12 is 2 × 3 × 2 × 2 = 24]

= 116/24 – 57/24 + 86/24

= (116 – 57 + 86)/24

= (202 – 57)/24

= 145/24



4. Simplify the fraction:

(i) 2 – 3/5      (ii) 4 + 7/8      (iii) 9/11 – 4/15      (iv) 8(1/2) – 3(5/8)


(i) 2 – 3/5

Solution:

2 – 3/5

= 2/1 – 3/5          [Since, 2 = 2/1]

= (2 × 5)/(1 × 5) – (3 × 1)/(5 × 1)           [Since, LCM of 1 and 5 is 5]

= 10/5 - 3/5

= (10 - 3)/5

= 7/5


(ii) 4 + 7/8

Solution:

4 + 7/8

= 4/1 + 7/8           [Since, 4 = 4/1]

= (4 × 8)/(1 × 8) + (7 × 1)/(8 × 1)           [Since, LCM of 1 and 8 is 8]

= 32/8 + 7/8

= (32 + 7)/8

= 39/8


(iii) 9/11 – 4/15

Solution:

9/11 – 4/15

LCM of 11 and 15 is 11 × 15 = 165.

= 9/11 - 4/15

= (9 × 15)/(11 × 15)

= (4 × 11)/(15 × 11)

= 135/165 – 44/165

= (135 – 44)/165

= 91/165


(iv) 8¹/₂ – 3⁵/₈

Solution:

8¹/₂ – 3⁵/₈

= 17/2 – 29/8

= (17 × 4)/(2 × 4) –(29 × 1)/(8 × 1)

[Since, LCM of 2 and 8 is 8]

= 68/8 – 29/8

= (68 – 29)/8

= 39/8

= 4⁷/₈



5. Simplify: 4²/₃ – 3¹/₄ + 2¹/₆.

Solution:

4²/₃ – 3¹/₄ + 2¹/₆.

= 14/3 – 13/4 + 13/6

= (14 × 4)/(3 × 4) – (13 × 3)/(14 × 3) + (13 × 2)/(6 × 2)

[Since, LCM of 3, 4 and 6 is 12, so we convert each fraction into an equivalent fraction with denominator 12]

= 56/12 – 39/12 + 26/12

= (56 – 39 + 26)/12

= (82 – 39)/12

= 43/12

= 3⁷/₁₂

Word Problems on Addition and subtraction of fractions:

1. Ron solved 2/7 part of an exercise while Shelly solved 4/5 of it. Who solved less? Solution:

In order to know who solved less part of the exercise, we will compare 2/7 and 4/5

LCM of denominators (i.e., 7 and 5) = 7 × 5 = 35

Converting each fraction in to an equivalent fraction having 35 as its denominator, we have

2/7 = (2 × 5 )/(7 × 5) = 10/35 and 4/5 = (4 × 7)/(5 × 7) = 28/35

Since, 10 < 28

Therefore, 10/35 < 28/35 => 2/7 < 4/5

Hence, Ron solved lesser part than Shelly.

2. Jack finished coloring a picture in 7/12 hour. Victor finished coloring the same picture in 3/4hour. Who worked longer? By what fraction was it longer?

Solution:

In order to know who worked longer, we will compare fractions 7/12 and 3/4.

LCM of 12 and 4 = 12

Converting each fraction into an equivalent fraction with 12 as denominator

7/12 = (7 × 1)/(12 × 1) = 7/12 and 3/4 = (3 × 3)/(4 × 3) = 9/12

Since, 7 < 9

Therefore, 7/12 < 9/12 => 7/12 < 3/4

Thus, Victor finished coloring in longer time.

Now, 3/4 - 7/12

= 9/12 – 7/12

= (9 – 7)/ 12

= 2/12

= 1/6

Hence, Victor finished coloring in 1/6 hour more time than Jack.

3. Sarah purchased 3¹/₂kg apples and 4³/₄ kg oranges. What is the total weight of fruits purchased by her?

Solution:

Total weight of the fruits purchased by Sarah is 3¹/₂ + 4³/₄ kg.

Now, 3¹/₂ + 4³/₄

= 7/2 + 19/4

= (7 × 2)/(2 × 2) + (19 × 1)/(4 × 1)

= 14/4 + 19/4

= (14 + 19)/4

= 33/4

= 8¹/₄

Hence, total weight is 8 1/4 kg.



4. Rachel ate 3/5 part of an apple and the remaining apple was eaten by her brother Shyla. How much part of the apple did Shyla eat? Who had the larger share? By how much?

Solution:

We have, Part of an apple eaten by Rachel = 3/5

Therefore, part of an apple eaten by Shyla = 1 - 3/5

= 5/5 – 3/5

= (5 - 3)/5

= 2/5

Clearly, 3/5 > 2/5

So, Rachel had the larger share.

Now,

3/5 – 2/5

= (3 - 2)/5

= 1/5

Therefore, Rachel had 1/5 part more than Shyla.



5. Sam wants to put a picture in a frame. The picture is 7³/₅ cm wide. To fit in the frame the picture cannot be more than 7³/₁₀ cm wide. How much the picture should be trimmed?

Solution:

Actual width of the picture = 7³/₅ cm = 38/5cm

Required width of the picture = 7³/₁₀ cm = 73/10 cm

Therefore, extra width = (38/5 – 73/10) cm

= (38 × 2)/(5 × 2) – (73 × 1)/( 10 × 1) cm

= 76/10 – 73/10 cm

= (76 – 73)/10 cm

= 3/10 cm

Hence, 3/10 cm width of the picture should be trimmed.

● Fractions

Fractions

Types of Fractions

Equivalent Fractions

Like and Unlike Fractions

Conversion of Fractions

Fraction in Lowest Terms

Addition and Subtraction of Fractions

Multiplication of Fractions

Division of Fractions

● Fractions - Worksheets

Worksheet on Fractions

Worksheet on Multiplication of Fractions

Worksheet on Division of Fractions

7th Grade Math Problems

From Addition and Subtraction of Fractions to HOME PAGE