Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Fraction of a Whole Numbers
Fraction is a part of a whole. The whole can be a single object or a collection of objects.
 |
 |
|
A Whole Cake |
A Collection of Apples |
Fraction of a whole numbers are explained here with 4 following examples.
(i)
There are three shapes:
(a) circle-shape
(b) rectangle-shape and
(c) square-shape
Each
one is divided into 4 equal parts. One part is shaded, i.e., one-fourth
of the shape is shaded and three parts of the shape is unshaded.
We say that, 1/4 of the shape is shaded and 3/4 of the shape is unshaded.
This 1/4 or 3/4 is a fraction or a fractional number.
1/4 = Out of 4 equal parts of a whole, one part is taken.
3/4 = Out of 4 equal parts of a whole, 3 parts are taken.
(ii) The rectangular shape is divided into 5 equal parts. 2 parts of this rectangle are shaded. The total parts of a whole are 5. Each equal part of the whole shape is 1/5. Two equal parts (shaded part) of the whole is 2/5. Three equal parts (unshaded parts) of the whole is 3/5.
2/5 means 2 parts out of 5 equal parts. We read it two-fifths or two by five.
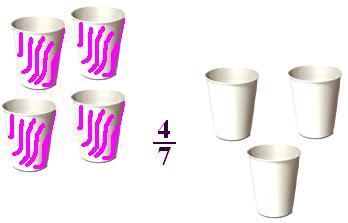
(iii) There is a collection of 7 glasses, of which 4 glasses are colorful.
Thus, 4/7 part of the collection of 7 glasses are coloured.
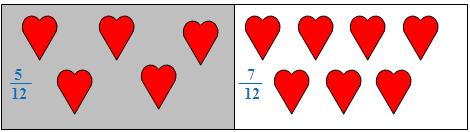
(iv) There are 12 hearts in a collection. 5 hearts are in shaded parts.
5 out of 12 hearts are in shaded portion and the rest 7 out of 12 hearts are in unshaded portion.
They represent 5/12 and 7/12 as fractions.
A fraction is a number written as a quotient of a pair of natural numbers.
For example; \(\frac{3}{4}\), \(\frac{5}{6}\), \(\frac{2}{8}\), etc.
The number written above the horizontal line is called Numerator.
The number written below the horizontal line is called Denominator.
In the fraction; \(\frac{3}{4}\)
3 is the Numerator and
4 is the Denominator.
The Numerator and Denominator are sometimes called as the terms of the fractions.
You might like these
To Convert a Percentage into a Fraction | Percentage into a Fraction
To convert a percentage into a fraction, place the given number over 100 and reduce it to its lowest term. Consider the following example: (i) 20% [We know % = 1/100]
Conversion of Mixed Fractions into Improper Fractions |Solved Examples
To convert a mixed number into an improper fraction, we multiply the whole number by the denominator of the proper fraction and then to the product add the numerator of the fraction to get the numerator of the improper fraction. I
Types of Fractions |Proper Fraction |Improper Fraction |Mixed Fraction
The three types of fractions are : Proper fraction, Improper fraction, Mixed fraction, Proper fraction: Fractions whose numerators are less than the denominators are called proper fractions. (Numerator < denominator). Two parts are shaded in the above diagram.
5th Grade Fractions | Definition | Examples | Word Problems |Worksheet
In 5th Grade Fractions we will discuss about definition of fraction, concept of fractions and different types of examples on fractions. A fraction is a number representing a part of a whole. The whole may be a single object or a group of objects.
Word Problems on Fraction | Math Fraction Word Problems |Fraction Math
In word problems on fraction we will solve different types of problems on multiplication of fractional numbers and division of fractional numbers.
Conversion of Improper Fractions into Mixed Fractions |Solved Examples
In conversion of improper fractions into mixed fractions, we follow the following steps: Step I: Obtain the improper fraction. Step II: Divide the numerator by the denominator and obtain the quotient and remainder. Step III: Write the mixed fraction
Equivalent Fractions | Fractions |Reduced to the Lowest Term |Examples
The fractions having the same value are called equivalent fractions. Their numerator and denominator can be different but, they represent the same part of a whole. We can see the shade portion with respect to the whole shape in the figures from (i) to (viii) In; (i) Shaded
Subtraction of Fractions having the Same Denominator | Like Fractions
To find the difference between like fractions we subtract the smaller numerator from the greater numerator. In subtraction of fractions having the same denominator, we just need to subtract the numerators of the fractions.
Comparison of Like Fractions | Comparing Fractions | Like Fractions
Any two like fractions can be compared by comparing their numerators. The fraction with larger numerator is greater than the fraction with smaller numerator, for example \(\frac{7}{13}\) > \(\frac{2}{13}\) because 7 > 2. In comparison of like fractions here are some
Comparison of Fractions having the same Numerator|Ordering of Fraction
In comparison of fractions having the same numerator the following rectangular figures having the same lengths are divided in different parts to show different denominators. 3/10 < 3/5 < 3/4 or 3/4 > 3/5 > 3/10 In the fractions having the same numerator, that fraction is
Worksheet on Comparison of Like Fractions | Greater & Smaller Fraction
In worksheet on comparison of like fractions, all grade students can practice the questions on comparison of like fractions. This exercise sheet on comparison of like fractions can be practiced
Like and Unlike Fractions | Like Fractions |Unlike Fractions |Examples
Like and unlike fractions are the two groups of fractions: (i) 1/5, 3/5, 2/5, 4/5, 6/5 (ii) 3/4, 5/6, 1/3, 4/7, 9/9 In group (i) the denominator of each fraction is 5, i.e., the denominators of the fractions are equal. The fractions with the same denominators are called
Representation of a Fraction | Numerator/Denominator | Simple Fraction
Representation of a fraction is discussed here. In a simple fraction, there is a horizontal line. Above this line we write a number which is called the numerator. Below this line we write another number which is called the denominator.
Worksheet on Fractions | Questions on Fractions | Representation | Ans
In worksheet on fractions, all grade students can practice the questions on fractions on a whole number and also on representation of a fraction. This exercise sheet on fractions can be practiced
Representations of Fractions on a Number Line | Examples | Worksheet
In representations of fractions on a number line we can show fractions on a number line. In order to represent 1/2 on the number line, draw the number line and mark a point A to represent 1.
![To convert a percentage into a fraction, place the given number over 100 and reduce it to its lowest term. Consider the following example: (i) 20% [We know % = 1/100]](/image-thumbnails/convert-a-percentage-into-a-fraction.png/default.webp)
Related Concept
● Representation of a Fraction
● Properties of Equivalent Fractions
● Comparison of Like Fractions
● Comparison of Fractions having the same Numerator
● Conversion of Fractions into Fractions having Same Denominator
● Conversion of a Fraction into its Smallest and Simplest Form
● Addition of Fractions having the Same Denominator
● Subtraction of Fractions having the Same Denominator
● Addition and Subtraction of Fractions on the Fraction Number Line
From Fraction of a Whole Numbers to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.