Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Like and Unlike Fractions
Like and unlike fractions are the two groups of fractions:
(i) 1/5, 3/5, 2/5, 4/5, 6/5
(ii) 3/4, 5/6, 1/3, 4/7, 9/9
In group (i) the denominator of each fraction is 5, i.e., the denominators of the fractions are equal.
The fractions with the same denominators are called like fractions.
In group (ii) the denominator of each fraction is different, i.e., the denominators of all the fractions are different.
The fractions with different denominators are called unlike fractions.
Examples of like fractions are:
(a) (2/9, 3/9, 5/9, 9/9);
(b) (3/10, 7/10, 1/10, 9/10);
(c) (1/7, 2/7, 4/7, 5/7, 7/7)
Examples unlike fractions are:
(a) (1/2, 1/4, 2/3, 5/6)
(b) (3/8, 2/3, 3/5, 2/7)
(c) (1/9, 2/7, 3/4, 2/5).
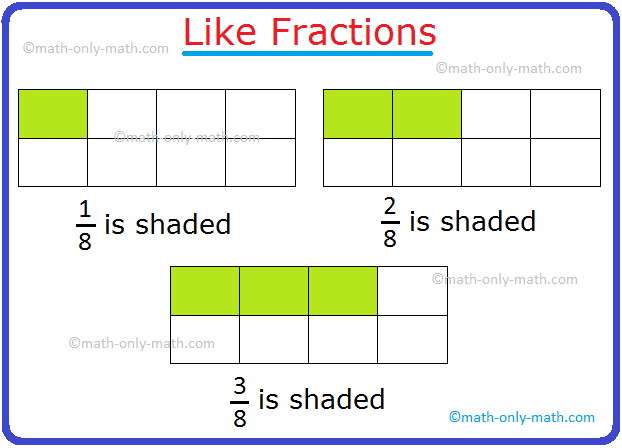
Like Fractions:
Observe the following figures.
The fraction \(\frac{1}{8}\), \(\frac{2}{8}\), \(\frac{3}{8}\) have the same denominator. Such fractions are called like fractions.
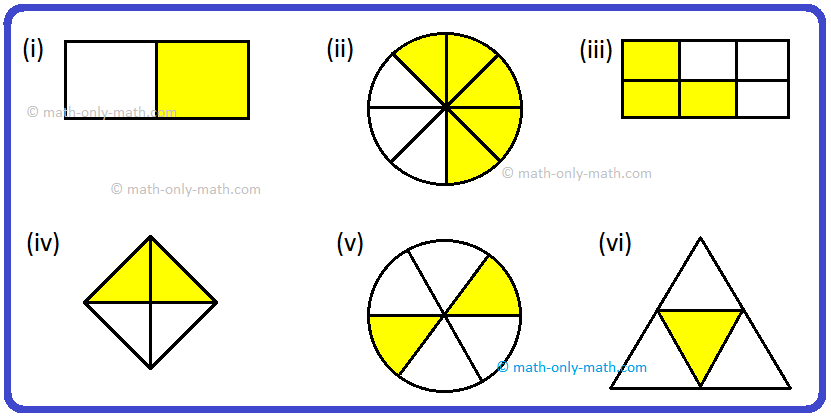
Unlike Fractions:
In figure (i) one part is shaded out of 3 parts, the fraction represented is \(\frac{1}{3}\).
In figure (ii) has two parts shaded out of 3 parts, the fraction represented is \(\frac{2}{5}\).
In figure (iii) we have three parts shaded out of 7 parts, the fraction represented is \(\frac{3}{7}\).
The fraction \(\frac{1}{3}\), \(\frac{2}{5}\), \(\frac{3}{7}\) have different denominators. Such fractions are called unlike fractions.
Conversion of Unlike Fractions into Like Fractions:
To convert an unlike fraction into a like fraction, we take LCM of all denominators of given fractions. Then we multiply both the numerator and the denominator by such a number so that the denominator becomes equal to LCM.
For Example:
Convert \(\frac{1}{7}\), \(\frac{3}{10}\) and \(\frac{4}{5}\) into like fractions.
First we find the LCM of denominators.
Therefore, the LCM of 7, 10 and 5 is 70.
Now, we have:
\(\frac{1}{7}\) = \(\frac{1 × 10}{7 × 10}\) = \(\frac{10}{70}\)
\(\frac{3}{10}\) = \(\frac{3 × 7}{10 × 7}\) = \(\frac{21}{70}\)
\(\frac{4}{5}\) = \(\frac{4 × 14}{5 × 14}\) = \(\frac{56}{70}\)
Hence, \(\frac{10}{70}\), \(\frac{21}{70}\) and \(\frac{56}{70}\) are the required like fractions.
Worksheet on Like and Unlike Fractions:
1. Which of the following is a set of like fractions?
|
(i) \(\frac{1}{9}\), \(\frac{5}{9}\), \(\frac{4}{9}\), \(\frac{11}{9}\) (iii) \(\frac{4}{11}\), \(\frac{5}{8}\), \(\frac{7}{9}\), \(\frac{1}{7}\) |
(ii) \(\frac{1}{7}\), \(\frac{2}{8}\), \(\frac{4}{19}\), \(\frac{7}{6}\) (iv) \(\frac{4}{11}\), \(\frac{5}{8}\), \(\frac{7}{9}\), \(\frac{1}{7}\) |
Answer:
1. (i) First set is like fractions because denominators are the same.
2. Which of the following is a set of unlike fractions?
|
(i) \(\frac{1}{13}\), \(\frac{13}{15}\), \(\frac{15}{17}\), \(\frac{17}{19}\) (iii) \(\frac{4}{16}\), \(\frac{1}{16}\), \(\frac{2}{16}\), \(\frac{9}{16}\) |
(ii) \(\frac{4}{12}\), \(\frac{5}{12}\), \(\frac{8}{12}\), \(\frac{9}{12}\) (iv) \(\frac{8}{9}\), \(\frac{1}{7}\), \(\frac{7}{8}\), \(\frac{8}{11}\) |
Answer:
2. (i) First and fourth sets are unlike fractions because denominators are not the same.
3. Convert the following unlike fractions into like fractions.
(i) \(\frac{3}{5}\), \(\frac{3}{10}\) and \(\frac{1}{20}\)
(ii) \(\frac{3}{8}\), \(\frac{5}{6}\) and \(\frac{7}{36}\)
(iii) \(\frac{2}{15}\), \(\frac{1}{45}\) and \(\frac{3}{25}\)
(iv) \(\frac{1}{2}\), \(\frac{3}{7}\) and \(\frac{7}{9}\)
Answer:
3. (i) \(\frac{12}{20}\), \(\frac{6}{20}\) and \(\frac{1}{20}\)
(ii) \(\frac{27}{72}\), \(\frac{60}{72}\) and \(\frac{14}{72}\)
(iii) \(\frac{30}{225}\), \(\frac{5}{225}\) and \(\frac{27}{225}\)
(iv) \(\frac{63}{126}\), \(\frac{54}{126}\) and \(\frac{98}{126}\)
Related Concept
● Representation of a Fraction
● Properties of Equivalent Fractions
● Comparison of Like Fractions
● Comparison of Fractions having the same Numerator
● Conversion of Fractions into Fractions having Same Denominator
● Conversion of a Fraction into its Smallest and Simplest Form
● Addition of Fractions having the Same Denominator
● Subtraction of Fractions having the Same Denominator
● Addition and Subtraction of Fractions on the Fraction Number Line
4th Grade Math Activities
From Like and Unlike Fractions to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.