Conversion of Improper Fractions into Mixed Fractions
In conversion of improper fractions into mixed fractions, we follow the following steps:
Step I: Obtain the improper fraction.
Step II: Divide the numerator by the denominator and obtain the quotient and remainder.
Step III: Write the mixed fraction as: QuotientRemainderDenominator.
To convert an improper fraction into a mixed number, divide the numerator of the given improper fraction by its denominator. The quotient will represent the whole number and the remainder so obtained will be the numerator of the fractional part. The denominator of the fractional part will be the same as that of the improper fraction i.e.,
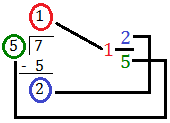
Let us convert 75 into a mixed number.
As you know if a fraction has same number as numerator and denominator, it makes a whole. Here in 75 we can take out 55 to make a whole and the remaining fraction we have is 25. So, 75 can be written in mixed numbers as 125.
55 = 1 + 25
75 = 55 + 25 = 1 + 25 = 125
|
Actually, 75 means 7 ÷ 5. When we divide 7 by 5 we get 1 as quotient and 2 as remainder. To convert an improper fraction into a mixed number we place the quotient 1 as the whole number, the remainder 2 as the numerator and the divisor 5 as the denominator of the proper fraction. |
Examples on Conversion of Improper Fractions into Mixed Fractions:
For Example:
1. Express each of the following improper fractions as mixed fractions:
(i) 174
We have,
Therefore, Quotient = 4, Remainder = 1, Denominator = 4.
Hence, 174 = 414
(ii) 135
We have,
Therefore, Quotient = 2, Remainder = 3, Denominator = 5.
Hence, 135 = 235
(iii) 285
We have,
Therefore, Quotient = 5, Remainder = 3, Denominator = 5
Hence, 285 = 535.
(iv) 289
We have,
Therefore, Quotient = 3, Remainder = 1, Denominator = 9
Hence, 289 = 319.
(v) 22615
We have,
Therefore, Quotient = 15, Remainder = 1, Denominator = 15
Hence, 22615 = 15115.
2. Convert each of the following improper fractions into mixed numbers.
(i) 157
(ii) 249
Solution:
(i)
(ii)
Conversion of an Improper Fraction Into a Mixed Fraction:
3. Let us convert 225 into an mixed fraction.
Divide the numerator 22 by the denominator 5.
The quotient 4 gives the whole number. The remainder 2 is the numerator of the fractions.
The denominator of the fraction remains the same. So, 225 = 425
4. Convert 413 into mixed fraction.
Divide the numerator 41 by the denominator 3.
The quotient 13 gives the whole number. The remainder 2 is the numerator of the fractions.
The denominator of the fraction remains the same.
So, 413 = 1323
Worksheet on Conversion of Improper Fractions into Mixed Fractions:
1. Convert the following into Improper Fractions:
(i) 119
(ii) 245
(iii) 268
(iv) 599
(v) 647
Answer:
1. (i) 129
(ii) 445
(iii) 328
(iv) 659
(v) 917
● Fraction
Representations of Fractions on a Number Line
Conversion of Mixed Fractions into Improper Fractions
Conversion of Improper Fractions into Mixed Fractions
Interesting Fact about Equivalent Fractions
Addition and Subtraction of Like Fractions
Addition and Subtraction of Unlike Fractions
Inserting a Fraction between Two Given Fractions
From Conversion of Improper Fractions into Mixed Fractions to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
How to Do Long Division? | Method | Steps | Examples | Worksheets |Ans
Apr 20, 25 11:46 AM
As we know that the division is to distribute a given value or quantity into groups having equal values. In long division, values at the individual place (Thousands, Hundreds, Tens, Ones) are dividend… -
Word Problems on Division | Examples on Word Problems on Division
Apr 20, 25 11:17 AM
Word problems on division for fourth grade students are solved here step by step. Consider the following examples on word problems involving division: 1. $5,876 are distributed equally among 26 men. H… -
Subtraction of 4-Digit Numbers | Subtract Numbers with Four Digit
Apr 20, 25 10:27 AM
We will learn about the subtraction of 4-digit numbers (without borrowing and with borrowing). We know when one number is subtracted from another number the result obtained is called the difference. -
Subtraction without Regrouping |4-Digit, 5-Digit & 6-Digit Subtraction
Apr 20, 25 10:25 AM
We will learn subtracting 4-digit, 5-digit and 6-digit numbers without regrouping. We first arrange the numbers one below the other in place value columns and then subtract the digits under each colum… -
Worksheets on Missing Numbers from 1 to 20 | Counting Missing Numbers
Apr 20, 25 10:17 AM
Printable worksheets on missing numbers from 1 to 20 help the kids to practice counting of the numbers.


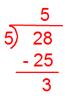
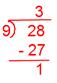
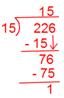


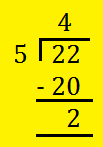
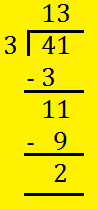
















New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.