Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Representation of a Fraction
Representation of a fraction is discussed here. In a simple fraction, there is a horizontal line. Above this line we write a number which is called the numerator.
Below this line we write another number which is called the denominator.
As, \(\frac{5}{7}\) → \(\frac{\textrm{Numerator}}{\textrm{Denominator}}\)
In a fraction, there are two numbers. One number is written above a horizontal line (i.e., 5) and the other is written below it (i.e., 7). The top part is called the numerator and the bottom part is called the denominator. The horizontal line between both the numbers is called the fraction bar.
Actually, a fraction can be expressed only when we know two facts.
(i) Total number of equal parts, a whole is divided into. This is the denominator.
(ii) Total number of equal parts of the whole being considered. This is the numerator.
For example, \(\frac{4}{7}\) means that the whole is divided into 7
equal parts. 4 parts of the same is considered. Here, 4 is the numerator and 7
is the denominator.
\(\frac{2}{5}\) is a fraction. 2 is the numerator and 5 is the denominator. The numbers like ½, 1/3, 2/3, ¼, ¾ are called the fractional numbers.
Again, \(\frac{5}{6}\) is a fraction, we say it as five upon six.
Similarly, 7/8, 4/12. 15/10, 326/429, etc., are fractions.
A fraction means a part of a number.
Note:
A fractional number is formed with a whole and its part or parts.
Writing and Reading Fractions:
We write fractions by looking at the number of equal parts and the number of parts we are referring to:
And it is read as three-fourths.
Questions and Answers on Representation of a Fraction:
1. Write the given fractions in words. One is done for you.
(i) \(\frac{2}{5}\) : two-fifth
(ii) \(\frac{1}{3}\) : __________
(iii) \(\frac{3}{4}\) : __________
(iv) \(\frac{5}{12}\) : __________
(v) \(\frac{3}{8}\) : __________
Answers:
(ii) One-third
(iii) Three-fourth
(iv) Five-twelveth
(v) Three-eightth
2. Give the fraction number for the given fractional names. One is done for you.
(i) Four-ninths : \(\frac{4}{9}\)
(ii) One-eighths : __________
(iii) One-fourths : __________
(iv) Six-thirteenths : __________
(v) Five-elevenths : __________
Answers:
(ii) \(\frac{1}{8}\)
(iii) \(\frac{1}{4}\)
(iv) \(\frac{6}{13}\)
(v) \(\frac{5}{12}\)
3. Write the fraction for the given. One has been done for you.
(i) Numerator = 7; Denominator = 9 → Fraction = \(\frac{7}{9}\)
(ii) Denominator = 8; Numerator = 3 → Fraction = __________
(iii) Numerator = 10; Denominator = 11 → Fraction = __________
(iv) Numerator = 8; Denominator = 15 → Fraction = __________
(v) Denominator = 15; Numerator = 11 → Fraction = __________
Answers:
(ii) \(\frac{3}{8}\)
(iii) \(\frac{10}{11}\)
(iv) \(\frac{8}{158}\)
(v) \(\frac{11}{15}\)
4. Identity the Numerator and denominator in the given fractions.
(i) \(\frac{1}{6}\) → Numerator = ______; Denominator = ______
(ii) \(\frac{3}{7}\) → Numerator = ______; Denominator = ______
(iii) \(\frac{12}{17}\) → Numerator = ______; Denominator = ______
(iv) \(\frac{9}{13}\) → Numerator = ______; Denominator = ______
Answers:
(i) Numerator = 1; Denominator = 6
(ii) Numerator = 3; Denominator = 7
(iii) Numerator = 12; Denominator = 17
(iv) Numerator = 9; Denominator = 13
Related Concept
● Representation of a Fraction
● Properties of Equivalent Fractions
● Comparison of Like Fractions
● Comparison of Fractions having the same Numerator
● Conversion of Fractions into Fractions having Same Denominator
● Conversion of a Fraction into its Smallest and Simplest Form
● Addition of Fractions having the Same Denominator
● Subtraction of Fractions having the Same Denominator
● Addition and Subtraction of Fractions on the Fraction Number Line
4th Grade Math Activities
From Representation of a Fraction to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
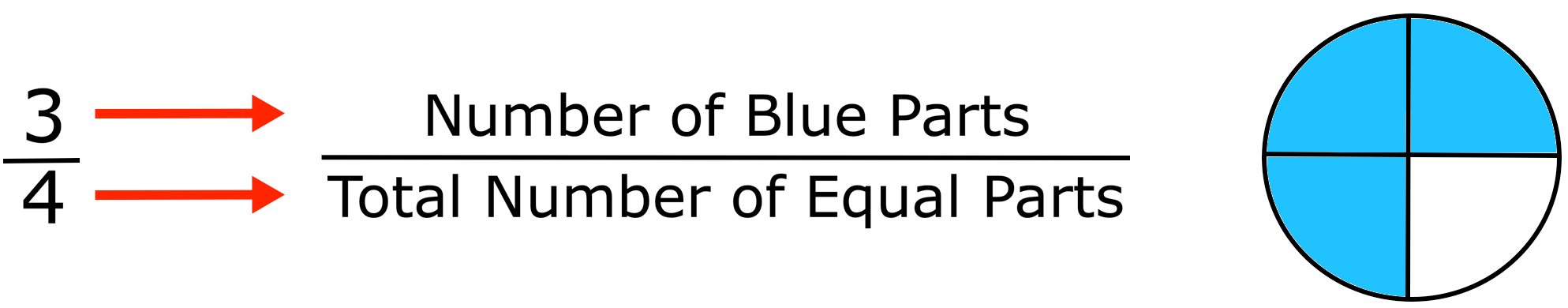

![To convert a percentage into a fraction, place the given number over 100 and reduce it to its lowest term. Consider the following example: (i) 20% [We know % = 1/100]](/image-thumbnails/convert-a-percentage-into-a-fraction.png/default.webp)




New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.