Comparison of Decimal Fractions
We will discuss here about the comparison of decimal fractions.
While comparing natural numbers we first compare total number of digits in both the numbers and if they are equal then we compare the digit at the extreme left. If they also equal then we compare the next digit and so on. We follow the same pattern while comparing the decimals.
✍️ We know that a decimal number has whole part and a decimal part. The decimal number with the greater whole part is greater.
For example, 5.4 is greater than 3.98.
✍️ If the whole parts are equal, first convert the given decimals into like decimals and then compare. We compare the digits in the tenths place. The decimal number with the greater digit in the tenths place is greater.
For example, 9.85 is greater than 9.65.
✍️ If the digits in the tenths place are equal, compare the digits in the hundredths place. The decimal number with the greater digit in the hundredths place is greater.
For example, 0.58 > 0.55.
✍️If the digits in the tenths and the hundredths place are same, the decimal number with the greater digit in the thousandths place is greater.
For example, 51.268 > 51.265
Examples on Comparing Decimals:
1. Compare 0.6 and 0.8.
Solution:
0.6 = 6 tenths
0.8 = 8 tenths
Because 8 tenths > 6 tenths
Thus, 0.8 > 0.6
2. Compare 0.317 and 0.341
Solution:
0.317 = 0.3 + 0.01 + 0.007
= 3 tenths + 1 hundredths + 7 thousandths
0.341 = 0.3 + 0.04 + 0.001
= 3 tenths +4 hundredths + 1 thousandths
Because 3 tenths = 3 tenths,
Now, compare next digit
1 hundredths < 4 hundredths
Thus, 0.317 < 0.341
Steps of Comparison of Decimal Fractions are given below:
Step I: First we need to observe the integral part.
For example:
(i) 104 < 140, this is how we check the integral part
(ii) 153 = 153
(iii) 112 > 121
Step II: When the integral part is same then compare the tenths place
For example:
(i) 1.4 < 1.9,
(ii) 1.5 = 1.50
(iii) 16.2 > 16.1
Step III: When the tenth place is same compare the hundredths place.
For example:
(i) 10.04 < 10.09,
(ii) 1.97 = 1.97
(iii) 71.92 > 71.90
In this way we first check the integral part and then move to the decimal places one by one.
For example:
1. Which is greater, 12.0193 or 102.01?
Solution:
First check the integer part
12 and 102
12 is < 102
102.01 is greater.
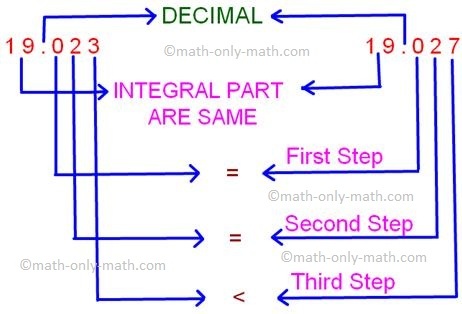
2. Which is smaller, 19.023 or 19.027?
Solution:
For each of these decimals the integral part is the same. So compare the tenths place. This is also same, check the hundredths places that is also same then move to the next decimal place.
Therefore, 19.023 < 19.027
So, 19.023 is smaller.
3. Find the greater number; 162.19 or 126.91.
Solution:
162.19 is greater than 126.91.
4. Which number is greater 293.82 or 293.62?
Solution:
First check the integer part,
293 = 293
Then the tenth place
8 > 6
Now the hundredth place
2 = 2
Therefore, 293.82 is greater than 293.62.
5. Find the greater number; 1432.97 or 1432.99
Solution:
First check the integer part,
1432 = 1432
Then the tenth place
9 = 9
Now the hundredth place
7 < 9
Therefore, 1432.99 is greater than 1432.97
6. Which number is greater 187.653 or 187.651?
Solution:
First check the integer part,
187 = 187
Then the tenth place
6 = 6
Then the hundredth place
5 = 5
Now the thousandth place
3 > 1
Therefore, 187.653 is greater than 187.651
7. Which number is greater 153.017 or 153.017?
Solution:
First check the integer part,
153 = 153
Then the tenth place
0 = 0
Then the hundredth place
1 = 1
Now the thousandth place
7 = 7
Therefore, 153.017 = 153.017
8. Find the greater number; 1324.42 or 1324.44
Solution:
First check the integer part,
1324 = 1324
Then the tenth place
4 = 4
Now the hundredth place
2 < 4
Therefore, 1324.44 is greater than 1324.42
9. Which number is greater 804.07 or 804.007?
Solution:
First check the integer part,
804 = 804
Then the tenth place
0 = 0
Then the hundredth place
7 > 0
Therefore, 804.07 is greater than 804.007
10. Find the greater number; 211.21 or 211.21
Solution:
First check the integer part,
211 = 211
Then the tenth place
2 = 2
Now the hundredth place
1 = 1
Therefore, 211.21 = 211.21
11. Write in ascending order using < sign:
(a) 43.81, 43.18, 43.08, 43.80
Solution:
43.08 < 43.18 < 43.80 < 43.81
(b) 89.09, 89.90, 89.01, 89.03
Solution:
89.01 < 89.03 < 89.09 < 89.90
(c) 53.35, 53.53, 53.30, 53.05
Solution:
53.05 < 53.30 < 53.35 < 53.53
(d) 61.16, 61.61, 61.06, 61.36
Solution:
61.06 < 61.16 < 61.36 < 61.61
12. Arrange the following decimal numbers in ascending order.
9.02; 2.56; 2.66; 8.02
Solution:
The greatest integral part is 9. So, 9.02 is the greatest number in the above set. 2.56 and 2.66 have equal integral parts, we compare the digits in the tenths place 5 > 6. So, 2.66 > 2.56.
The decimal numbers in ascending order are 2.56; 2.66; 8.02; 9.02
13. Compare and put the appropriate sign:
(i) 13.6 ______ 1.36
(ii) 65.010 ______ 65.110
(iii) 209.008 ______ 210.007
(iv) 47.981 ______ 29.999
Solution:
(i) >
(ii) <
(iii) <
(iv) >
Working Rules for Comparison of Decimals:
Step I: Compare the whole parts of the given numbers. The number with greater whole part will be greater. If the whole parts are equal, go to next step.
Step II: Compare the extreme left digits of the decimal parts of two numbers. The number with greater extreme left digit will be greater. If the extreme left digits of decimal parts are equal, then compare the next digits and so on.
Solved Examples:
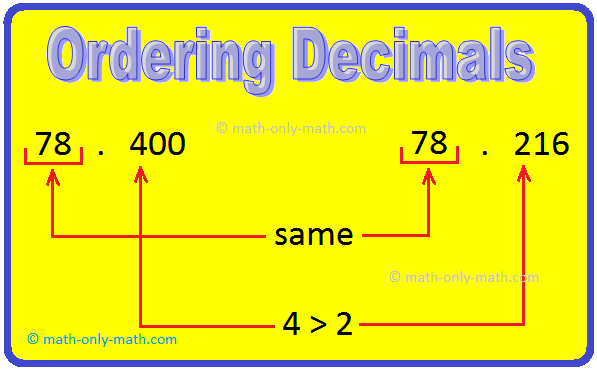
1. Which decimal is greater 78.40 or 78.216?
Solution:
Converting the given decimals into like decimals
78.40 = 78.400
78.216 = 78.216
Therefore, 78.400 > 78.216
Thus, 78.40 > 78.216
2. Which is greater 35.40 or 35.209?
Solution:
Given decimals are 35.40 and 35.209.
Converting of the given decimals into like decimals, we have
35.40 = 35.400
35.209 = 35.209
Therefore, 35.400 > 35.209
Thus, 35.40 > 35.209
How to compare decimal numbers?
How to compare decimal numbers?
Answer:
While comparing decimals, first we compare the whole number part (if any). The decimal having greater whole number part is greater and if decimal having smaller whole number part is smaller We compare the decimal part of a decimal number if its whole number parts are equal
For Example:
Compare the decimals.
(i) 3.43, 4.12
(ii) 6.87, 6.12
Solution:
(i) Compare the whole number part i.e. 3 < 4
So, 3.43 < 4.12
(ii) The whole number parts are equal. Compare the first decimal place
i.e., 8 tenths > 1 tenths
So, 6.87 > 6.12
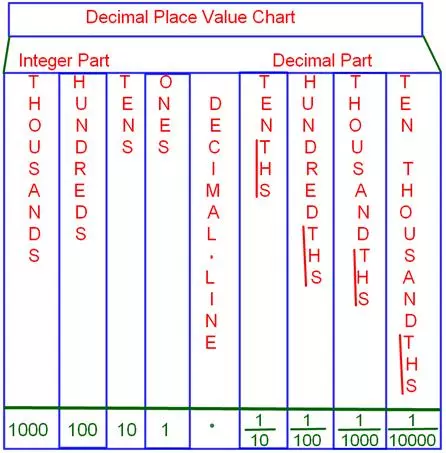
● Decimal.
Expanded form of Decimal Fractions.
Changing Unlike to Like Decimal Fractions.
Comparison of Decimal Fractions.
Conversion of a Decimal Fraction into a Fractional Number.
Conversion of Fractions to Decimals Numbers.
Addition of Decimal Fractions.
Problems on Addition of Decimal Fractions
Subtraction of Decimal Fractions.
Problems on Subtraction of Decimal Fractions
Multiplication of a Decimal Numbers.
Multiplication of a Decimal by a Decimal.
Properties of Multiplication of Decimal Numbers.
Problems on Multiplication of Decimal Fractions
Division of a Decimal by a Whole Number.
Division of Decimal Fractions by Multiples.
Division of a Decimal by a Decimal.
Division of a whole number by a Decimal.
Properties of Division of Decimal Numbers
Problems on Division of Decimal Fractions
Conversion of fraction to Decimal Fraction.
From Comparison of Decimal Fractions to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Subtraction of Decimals | Subtracting Decimals | Decimal Subtraction
Apr 24, 25 03:25 PM
We will discuss here about the subtraction of decimals. Decimals are subtracted in the same way as we subtract ordinary numbers. We arrange the digits in columns -
How to Do Long Division? | Method | Steps | Examples | Worksheets |Ans
Apr 24, 25 10:18 AM
As we know that the division is to distribute a given value or quantity into groups having equal values. In long division, values at the individual place (Thousands, Hundreds, Tens, Ones) are dividend… -
Division by Two-Digit Numbers | Knowledge of Estimation | Division
Apr 24, 25 10:12 AM
In division by two-digit numbers we will practice dividing two, three, four and five digits by two-digit numbers. Consider the following examples on division by two-digit numbers: Let us use our knowl… -
Addition of Decimals | How to Add Decimals? | Adding Decimals|Addition
Apr 24, 25 01:45 AM
We will discuss here about the addition of decimals. Decimals are added in the same way as we add ordinary numbers. We arrange the digits in columns and then add as required. Let us consider some -
Addition of Like Fractions | Examples | Videos | Worksheet | Fractions
Apr 23, 25 09:23 AM
To add two or more like fractions we simplify add their numerators. The denominator remains same. Thus, to add the fractions with the same denominator, we simply add their numerators and write the com…














New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.