Addition of Like Fractions

To add two or more like fractions we simplify add their numerators. The denominator remains same.

1. Let us find the sum of two fractions \(\frac{3}{7}\) and \(\frac{2}{7}\).

\(\frac{3}{7}\) is colored green.

\(\frac{2}{7}\) is colored yellow.

\(\frac{3}{7}\) + \(\frac{2}{7}\) is represented by 

\(\frac{3}{7}\) + \(\frac{2}{7}\)

= \(\frac{3 + 2}{7}\)

= \(\frac{5}{7}\) = \(\frac{\textrm{Sum of Numerators}}{\textrm{Common Denominator}}\)

Addition of Like Fractions Video

Subscribe to our YouTube channel for the latest videos, updates, and tips.

Addition of Fractions with the Same (Like) Denominator

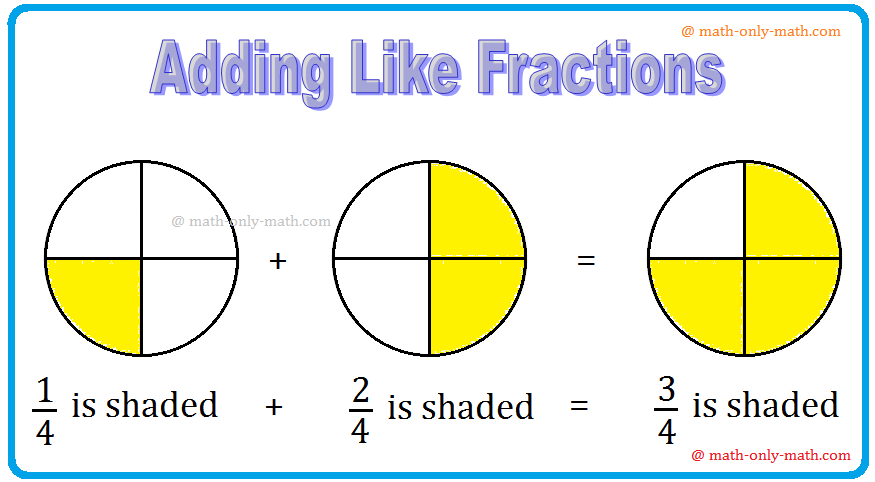
2. Observe the following figures:

What do we observe?

In the first figure \(\frac{1}{4}\)of the circle is shaded and in the second figure \(\frac{2}{4}\) of the circle is shaded.

In all, we have Hence 3/4 of the circle is shaded.

\(\frac{1}{4}\) + \(\frac{2}{4}\) = \(\frac{1 + 2}{4}\) = \(\frac{3}{4}\)

Thus, to add the fractions with the same denominator, we simply add their numerators and write the common denominator.

Sum of the fractions with like denominators = \(\frac{\textrm{Sum of the Numerators}}{\textrm{Common Denominator}}\)

Solved Examples on Addition of Like Fractions:

1. Find the sum of \(\frac{1}{9}\) and \(\frac{4}{9}\).

Solution:

Sum of \(\frac{1}{9}\) and \(\frac{4}{9}\)

= \(\frac{1}{9}\) + \(\frac{4}{9}\)

= \(\frac{1 + 4}{9}\)

= \(\frac{5}{9}\)

2. Find the sum of \(\frac{7}{27}\) and \(\frac{9}{27}\).

Solution:

Sum of \(\frac{7}{27}\) and \(\frac{9}{27}\)

= \(\frac{7}{27}\) + \(\frac{9}{27}\)

= \(\frac{7 + 9}{27}\)

= \(\frac{16}{27}\)

3. Find the sum of \(\frac{4}{29}\), \(\frac{5}{29}\) and \(\frac{8}{29}\).

Solution:

Sum of \(\frac{4}{29}\), \(\frac{5}{29}\) and \(\frac{8}{29}\).

= \(\frac{4}{29}\) + \(\frac{5}{29}\) + \(\frac{8}{29}\)

= \(\frac{4 + 5 + 8}{29}\)

= \(\frac{17}{29}\)

More Examples on Addition of Like Fractions:

(Fractions having same denominator)

4. Add \(\frac{5}{17}\) + \(\frac{4}{17}\)

Solution:

\(\frac{5}{17}\) + \(\frac{4}{17}\)

= \(\frac{5 + 4}{17}\)

= \(\frac{9}{17}\)  (in lowest terms)

5. Add \(\frac{3}{23}\) + \(\frac{13}{23}\) + \(\frac{4}{23}\)

Solution:

\(\frac{3}{23}\) + \(\frac{13}{23}\) + \(\frac{4}{23}\)

= \(\frac{3 + 13 + 4}{23}\)

= \(\frac{20}{23}\)  (in lowest terms)

Addition of Three Like Fractions Video

Subscribe to our YouTube channel for the latest videos, updates, and tips.

6. Find the sum of \(\frac{31}{105}\), \(\frac{41}{105}\) and \(\frac{11}{105}\).

Solution:

Sum of \(\frac{31}{105}\), \(\frac{41}{105}\) and \(\frac{11}{105}\).

= \(\frac{31}{105}\) + \(\frac{41}{105}\) + \(\frac{11}{105}\).

= \(\frac{31 + 41 + 11}{105}\)

= \(\frac{83}{105}\)

7. Find the sum of \(\frac{3}{7}\) and \(\frac{2}{7}\)

Solution:

\(\frac{3}{7}\) + \(\frac{2}{7}\) = \(\frac{3 + 2}{7}\) = \(\frac{5}{7}\)

2. Find the sum of \(\frac{1}{15}\), \(\frac{4}{15}\), \(\frac{7}{15}\)

Solution:

\(\frac{1}{15}\) + \(\frac{4}{15}\) + \(\frac{7}{15}\) = \(\frac{1 + 4 + 7}{15}\) = \(\frac{12}{15}\)

Worksheet on Addition of Like Fractions:

1. Add the following Like Fractions:

(i) \(\frac{2}{5}\) + \(\frac{3}{5}\)

(ii) \(\frac{1}{8}\) + \(\frac{3}{8}\) + \(\frac{7}{8}\)

(iii) \(\frac{11}{23}\) + \(\frac{10}{23}\) + \(\frac{5}{23}\)

(iv) \(\frac{2}{10}\) + \(\frac{1}{10}\) + \(\frac{3}{10}\)

(v) \(\frac{5}{11}\) + \(\frac{7}{11}\) + \(\frac{4}{11}\) + \(\frac{2}{11}\)

Answer:

1. (i) 1

(ii) 1\(\frac{3}{8}\)

(iii) 1\(\frac{3}{23}\) 

(iv) \(\frac{3}{5}\) 

(v) 1\(\frac{7}{11}\) 

2. Find the sum:

(i) \(\frac{1}{9}\) + \(\frac{4}{9}\)

(ii) \(\frac{1}{4}\) + \(\frac{2}{4}\)

(iii) \(\frac{5}{21}\) + \(\frac{8}{21}\)

(iv) \(\frac{4}{15}\) + \(\frac{7}{15}\)

(v) \(\frac{7}{16}\) + \(\frac{8}{16}\)

(vi) \(\frac{13}{19}\) + \(\frac{2}{19}\)

Answer:

2. (i) \(\frac{5}{9}\)

(ii) \(\frac{3}{4}\)

(iii) \(\frac{13}{21}\)

(iv) \(\frac{11}{15}\)

(v) \(\frac{15}{16}\)

(vi) \(\frac{15}{19}\)

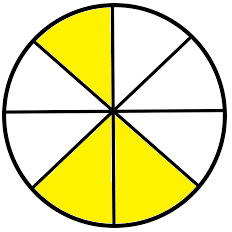
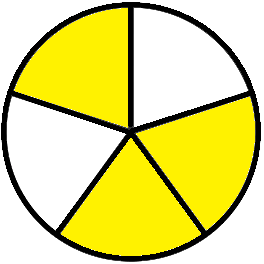
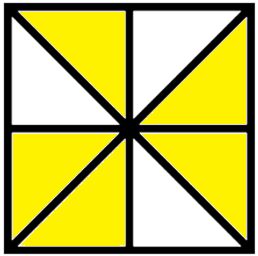
3. Using the figures, fill in the blanks:

(i)		\(\frac{1}{8}\) + \(\frac{2}{8}\) = \(\frac{--- + ---}{8}\) = \(\frac{---}{8}\)
(ii)		\(\frac{1}{5}\) + \(\frac{2}{5}\) = \(\frac{--- + ---}{5}\) = \(\frac{---}{5}\)
(iii)		\(\frac{1}{8}\) + \(\frac{2}{8}\) + \(\frac{2}{8}\) = \(\frac{--- + --- + ---}{8}\) = \(\frac{---}{8}\)
(iv)		\(\frac{2}{7}\) + \(\frac{4}{7}\) = \(\frac{--- + ---}{7}\) = \(\frac{---}{7}\)

4th Grade Math Activities

From Addition of Like Fractions to HOME PAGE