Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Fraction as a Part of Collection
How to find fraction as a part of collection?
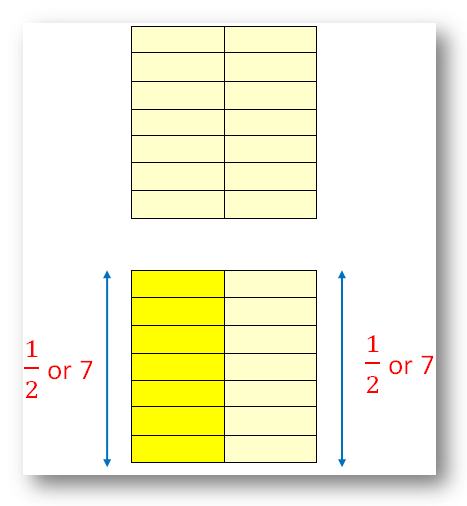
Let there be 14 rectangles forming a box or rectangle.
Thus, it can be said that there is a collection of 14 rectangles, 2 rectangles in each row.
If it is folded into two halves,
each half will have 7 rectangles. So, we can say one-half of 14 is 7.
Similarly, one- half of 8 is 4 and one-half of 16 is 8.
One-half of 8 squares = 4
Thus, 1/2 = 4/8
That is, out of two equal parts, one part is 1.
Out of two equal parts of 8 one part is 4
|
One-half of a collection of 8 cups = 4 cups
Thus, 1/2 = 4/8
1 and 4 are numerators 2 and 8 are denominators |
The denominator or bottom number
of a fraction is the number of equal parts of a whole or a collection. The numerator
or top number of a fraction means how many equal parts of a whole or a
collection is considered.
3/5, 7/8, 2/3, 5/12, 7/16, 11/25, 6/15 are all fractions.
The top numbers of these fractions are 3, 7, 2, 5, 7, 11 and 6. These numbers are called top numbers or numerators of the related fractions.
The bottom numbers of these fractions are 5, 8, 3, 12, 16, 25 and 15. These numbers are called bottom numbers or denominators of the related fractions.
If we have 2 bananas in a basket counting 7 fruits. How many fruits have we in our whole set? How many bananas have we in our whole set?
We have 2 bananas out of 7 fruits which can be written as \(\frac{2}{7}\).
In the figure below, the strip has been divided in 8 equal parts. 3 parts of the strip are shaded. The shaded part represents three-eight of the strip. We write this as \(\frac{3}{8}\).
Number of unshaded parts are 5. Therefore, the unshaded part represents five-eight of this strip. We write this as \(\frac{5}{8}\).
In the fraction \(\frac{3}{8}\), 3 represents the shaded part of the collection and the 8 represents the total number of parts. 3 is numerator and 8 is denominator of this fraction \(\frac{3}{8}\).
A fraction is made up of two parts-numerator and denominator. The numerator is written above the denominator separated by a short line.
Fractions also refer part of the whole collection or group.
|
Look at the picture- It is a collection of 3 flowers. How many are blue? 2 out of the 3 flowers are blue. \(\frac{2}{3}\) \(\frac{\textrm{Blue Flowers (Part of Collection)}}{\textrm{Total Flowers (The Whole Collection)}}\) \(\frac{2}{3}\) of the flowers are blue. |
|
There are four cars in all. 3 cars are blue, 1 car is red. So, we can say - \(\frac{1}{4}\) car is red and \(\frac{3}{4}\) cars are blue |
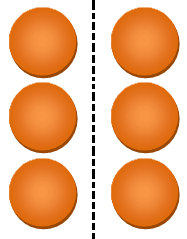
The figure given below is a collection of 6 circles.
Draw a dotted line to divide the collection into two equal parts. Then, each part represents 3 circles. Also, each part contains 1/2
Hence 1/2 of 6 =3.
The figure given below is a collection of 8 circles.
Draw dotted lines to divide the collection into 4 equal parts.
Now, each part represents 1/4. Also, each part contains 2 circles.
Hence, 1/4 of 8 = 2.
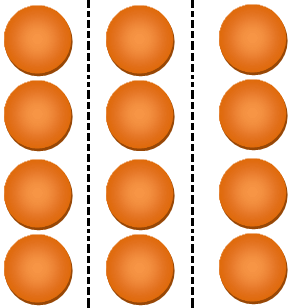
The figure below contains 12 circles.
Draw dotted lines to divide the collection into 3 equal parts.
Then each part represents 1/3.
Also, each part contains 4 circles.
Hence, 1/3 of 12 =4.
2 parts of the collection represent 2/3.
Also, 2 parts contain 8 circles.
Hence, 2/3 of 12 = 8.
Finding Fraction of a Collection:
Finding \(\frac{1}{2}\) of a collection
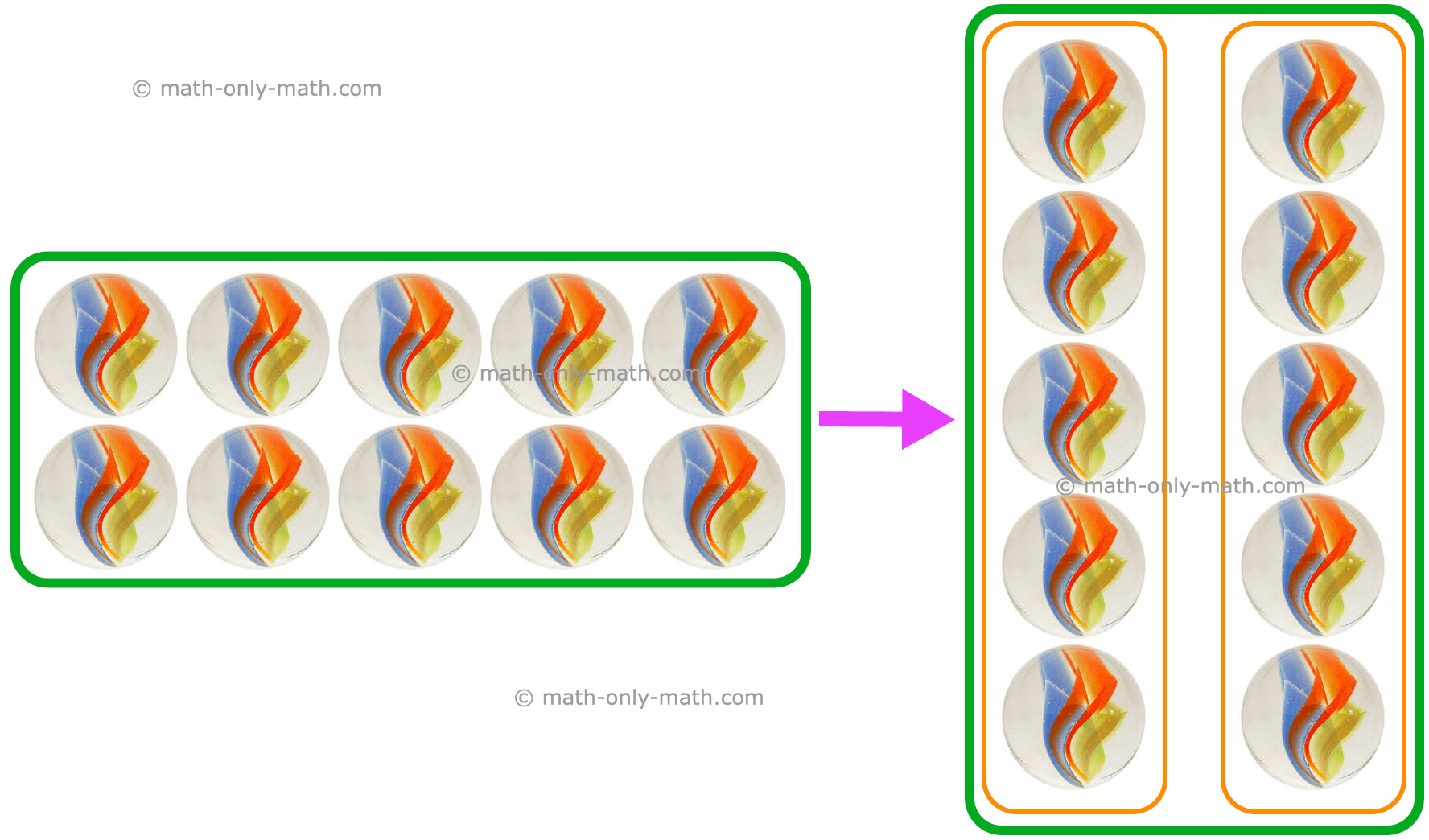
Michael and Jennifer are sharing, help them to divide these marbles equally.
Equally means dividing into two equal parts, which means dividing by 2.
i.e., 8 ÷ 2 = 4 or \(\frac{1}{2}\) of 8 is 4.
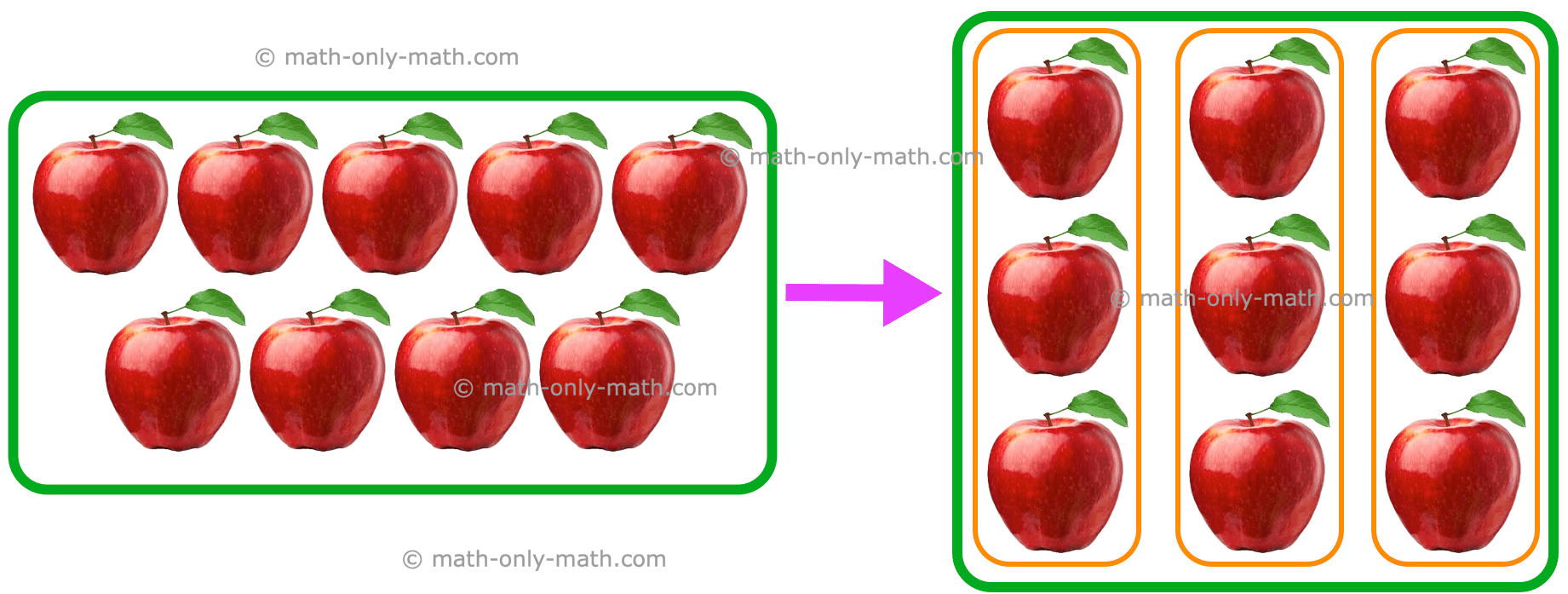
Finding \(\frac{1}{3}\) of a collection
One-third is 1 part of 3 equal parts.
Dividing into three equal parts also means dividing by 3.
i.e., 9 ÷ 3 = 3 or \(\frac{1}{3}\) of 9 is 3.
Related Concepts
● Fraction as a Part of a Whole
● Convert a Fraction to an Equivalent Fraction
● Proper Fraction and Improper Fraction
From Fraction as a Part of Collection to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.

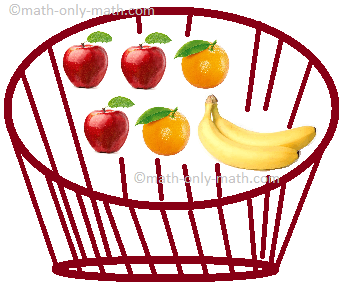




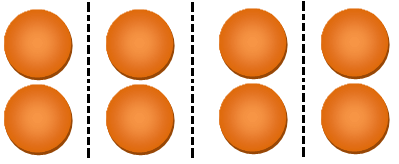
![To convert a percentage into a fraction, place the given number over 100 and reduce it to its lowest term. Consider the following example: (i) 20% [We know % = 1/100]](/image-thumbnails/convert-a-percentage-into-a-fraction.png/default.webp)




New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.