Fraction in Lowest Terms
Fraction in lowest terms is discussed here.
If numerator and denominator of a fraction have no common factor other than 1(one), then the fraction is said to be in its simple form or in lowest term.
In other words, a fraction is in its lowest terms or in lowest form, if the HCF of its numerator and denominator is 1.
Definition of Fraction in Lowest Terms:
A fraction is said to be in the lowest term or the simplest form, if the HCF of numerator an denominator is 1, i.e., the numerator and denominator are not further divisible by are common number.
For example, fractions 12, 23, 34, 513 are all in their lowest terms.
Consider the equivalent fractions:
23, 46, 69, 812, 1015 ........
That is , 10÷515÷5 = 23; 1015 = 23
8÷412÷4 = 23; 812 = 23
6÷39÷3 = 23; 69 = 23
23 is the simplest form of the fraction 1015 or 812 or 69
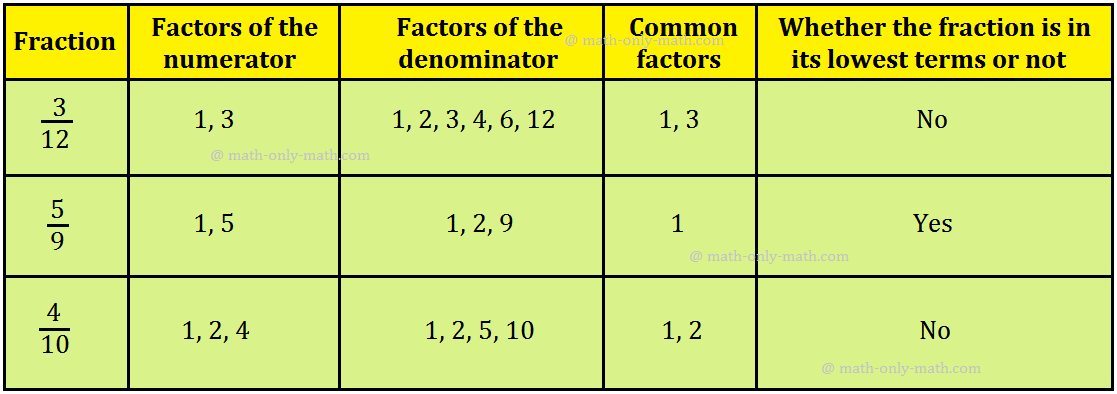
A fraction is in the lowest terms if the only common factor of the numerator and denominator is 1.
Observe the fractions represented by the colored portion in the following figures.
In figure A colored part is represented by fraction 816.
The colored part in figure B is represented by fraction 48.
In figure C the colored part represents the fraction 24 and
In figure D colored part represents 12.
When numerator and denominator of fraction 816 are divided by 2. We get 48 and in the same way 48 gives 24 and then 12.
So, we find that 816, 48, 24 are equal to fraction for 12. Thus, 12 is the simplest or lowest form of all its equivalent fractions like 24, 48, 816, 1632, 3264, …… etc.
Now, if we take all the factors of the numerator 8 and denominator 16 of the fraction 816, we get the following:
All factors of 8 are 1, 2, 4, 8.
All factors of 16 are 1, 2, 4, 8, 16.
We find that highest common factor (HCF) of 8 and 16 is 8.
On dividing both numerator and denominator by highest common factor we get 12.
Since, both numerator and denominator of fraction 12 have no common factor other than 1, we say that the fraction 12 is in its lowest terms or simplest form.
A fraction is said to be in its simplest form when its numerator and denominator do not have any common factor except 1.
Observe the following:
To reduce a fraction to its lowest terms, we divide the numerator and the denominator by their common factors till only 1 is left as the common factor.
There are two methods to reduce a given fraction to its simplest form, viz., H.C.F. Method and Prime Factorization Method.
I. H.C.F. Method:
Find the H.C.F. of the numerator and denominator of the given fraction.
In order to reduce a fraction to its lowest terms, we divide its numerator and denominator by their HCF.
Example to Reduce a Fraction in Lowest Term, using H.C.F. Method:
1. Reduce the fraction 2156 to its simplest form.
Solution:
Therefore H.C.F. of 21 and 56 is 7.
We now divide the numerator and denominator of the given fraction by 7.
2156 = 21÷756÷7 = 38.
2. Reduce 4864 to its lowest form.
Solution:
First we find the HCF of 48 and 64 by factorization method.
The factors of 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48.
The factors of 64: 1, 2, 4, 8, 16, 32, and 64.
The common factors of 48 and 64 are: 1, 2, 4, 8, 12 and 16.
Therefore, HCF of 48 and 64 is 16.
Now 4864 = 48÷1664÷16
[Dividing numerator and denominator by the HCF of 48 and 64 i.e., 16]
⇒ 4864 = 34
3. Reduce 4472 to its lowest form.
Solution:
First we find the HCF of 44 and 72 by factorization method.
The factors of 44: 1, 2, 4, 11, 22 and 44.
The factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, and 36.
The common factors of 44 and 72 are: 1, 2 and 4.
Therefore, HCF of 44 and 72 is 4.
Now 4472 = 44÷472÷4
[Dividing numerator and denominator by the HCF of 44 and 72 i.e., 4]
⇒ 4472 = 1118
To change a fraction to lowest terms:
4. Reduce 1015 to its lowest terms:
Solution:
Step I:
Find the largest common factor of 10 and 15.
Factors of 10: 1, 2, 5, 10
Factors of 15: 1, 3, 5, 15
Common factors: 1, 5
H.C.F of 10 and 15 = 5
Step II:
Divide both the numerator and denominator by the H.C.F.
10÷515÷5 = 23
Therefore, 1015 = 23 (in its lowest terms)
5. Reduce 1845 to its lowest terms.
To express a fraction in its lowest term, we divide the numerator and denominator by their HCF.
6. Reduce these fractions in their lowest terms.
(i) 628
(ii) 2474
Solution:
(i) In 628 numerator is 6 and denominator is 28.
Let us find the HCF of 6 and 28.
Factors of 6 are 1, 2, 3 and 6.
Factors of 28 are 1, 2, 4, 7, 14 and 28.
Common factors of 6 and 28 are 1 and 2.
HCF of 6 and 28 is 2.
Thus, 628 = 5÷228÷2 = 314
Thus, 314 the simplest form or lowest term of 628.
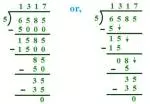
(ii) In 2474 numerator is 24 and denominator is 74.
Let us find the HCF of 24 and 74 by long division method:
24) 74 (3
- 72
2 ) 24 (12
- 24
0
HCF of 24 and 74 is 2.
Thus, 2474 = 24÷274÷2 = 1237
Hence, 1237 is the simplest form or lowest term of 2474
II. Prime Factorization Method:
Express both numerator and denominator of the given fraction as the product of prime factors and then cancel the common factors from them.
Example to reduce a fraction in lowest term, using Prime Factorization Method:
1. Reduce 120360 to the lowest term.
Solution:
120 = 2 × 2 × 2 × 3 × 5 = 1
360 2 × 2 × 2 × 3 × 3 × 5 3
Solve Examples on Reducing Fractions to Lowest Terms:
1. Express 28140 in the simplest form.
Solution:
Let us find all the factors of both numerator and denominator.
Factors of 28 are 1, 2, 4, 7, 14, 28
Factors of 140 are 1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, 140
The highest common factor is 28. Now dividing both numerator and denominator by 28, we get 15. The numerator 1 and denominator 5 have no common factors other than 1. So, 15 is the simplest form of 28140.
2. Is 48168 in its simplest form?
Solution:
Let us find HCF of numerator and denominator and then divide both by the highest common factor.
The highest common factor is 2 × 2 × 2 × 3 = 24
Let us divide both numerator and denominator by 24. We get 27.
So, the fraction 48168 is not in its simplest form.
Simplifying a Fraction:
3. Simplify 4284
Method I:
|
Steps I: Divide numerator and denominator by 2. 42 ÷ 2 = 21; 84 ÷ 2 = 42; we get 2142 Steps II: Divide 21 and 42 by 3. 21 ÷ 3 = 7; 42 ÷ 3 = 14; we get 714 Steps III: Divide 7 and 14 by 7. 7 ÷ 7 = 1; 14 ÷ 7 = 2; we get 12 Therefore, 4284 = 12, in its lowest terms |
Now divide the numerator and denominator by the H.C.F. i.e., 42
42÷4284÷42 = 12 in its lowest terms.
4. Express each of the following fractions to its lowest terms:
(i) 1827
(ii) 3070
Solution:
(i) We have, 18 = 2 × 3 × 3
27 = 3 × 3 × 3
So, we can divide the numerator and the denominator by 3 × 3 = 9
So, 18÷927÷9 = 23
Thus, the simplest form of 1827 is 23
(ii) We have, 30 = 2 × 3 × 5
70 = 2 × 5 × 7
So, can divide the numerator and denominator by 2 × 5 = 10
So 30÷1070÷10 = 37
Thus, the simplest form of 3070 is 37
5. Reduce 120360 its lowest terms.
Solution:
We can divide the numerator and the denominator step by step, by their common factors.
So, 120÷2360÷2 = 60÷2180÷2 = 30÷390÷3 = 10÷230÷2 = 5÷515÷5 = 13
Therefore, 120360 equal to 13 its lowest terms.
Worksheet on Reduce a Fraction to its Simplest Form:
1. Convert the given fractions in lowest form:
(i) 24
(ii) 39
(iii) 416
(iv) 1215
(v) 728
(vi) 610
(vii) 972
(viii) 2436
Answers:
1. (i) 12
(ii) 13
(iii) 14
(iv) 45
(v) 14
(vi) 35
(vii) 18
(viii) 23
2. Reduce the following fractions to their lowest terms.
(i) 1260
(ii) 13169
(iii) 735
(iv) 1228
(v) 327
(vi) 80100
(vii) 1418
(viii) 2958
(ix) 963
(x) 90128
Answer:
2. (i) 15
(ii) 113
(iii) 15
(iv) 37
(v) 19
(vi) 45
(vii) 79
(viii) 12
(ix) 17
(x) 4564
3. Write the fraction which is in the lowest terms in each set of equivalent fractions.
(i) [1565, 313, 30130]
(ii) [19, 872, 545]
(iii) [5070, 57, 2535]
(iv) [311, 33121, 1555]
Answer:
3. (i) 313
(ii) 19
(iii) 57
(iv) 311
4. State true or false:
(i) 58 = 558
(ii) 648 = 18
(iii) 69 = 4875
(iv) 78 = 910
(v) 86 = 2821
Answer:
4. (i) False
(ii) True
(iii) False
(iv) False
(v) False
5. Match the given fractions:
|
(i) 1215 (ii) 69 (iii) 836 (iv) 2432 (v) 1525 |
(a) 34 (b) 29 (c) 35 (d) 45 (e) 23 |
Answers:
5.
|
(i) 1215 (ii) 69 (iii) 836 (iv) 2432 (v) 1525 |
(d) 45 (e) 23 (b) 29 (a) 34 (c) 35 |
6. Write the fraction for given statements and convert them to the lowest form.
|
Statement |
Fraction |
Lowest Form |
|
(i) Ten minutes to an hour | ||
|
(ii) Amy ate 3 out of the 9 slices of a pizza | ||
|
(iii) Eight months to a year | ||
|
(iv) Kelly colored 4 out of 12 parts of a drawing | ||
|
(v) Jack works for 8 hours in a day. |
Answers:
6.
|
Statement |
Fraction |
Lowest Form |
|
(i) Ten minutes to an hour |
5060 |
56 |
|
(ii) Amy ate 3 out of the 9 slices of a pizza |
39 |
13 |
|
(iii) Eight months to a year |
812 |
23 |
|
(iv) Kelly colored 4 out of 12 parts of a drawing |
412 |
13 |
|
(v) Jack works for 8 hours in a day. |
824 |
13 |
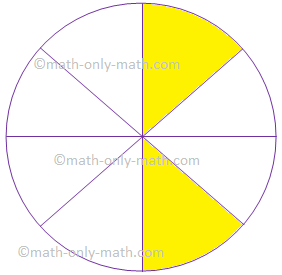
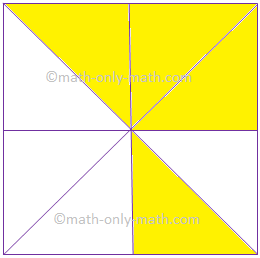
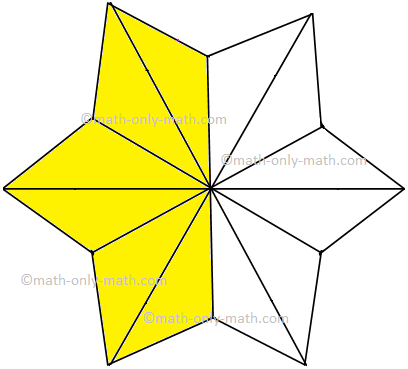
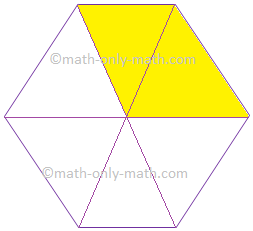
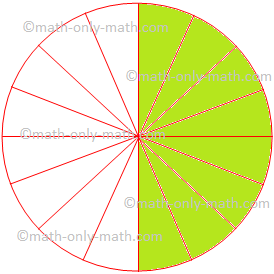
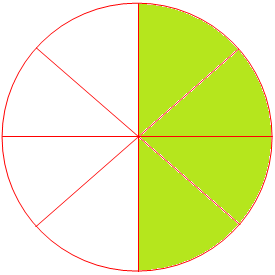
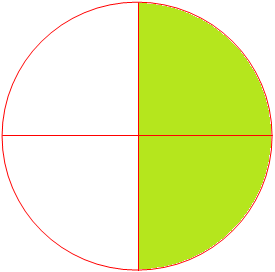
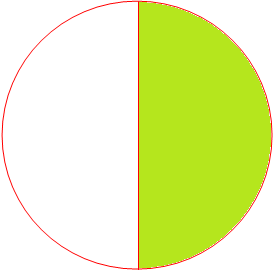
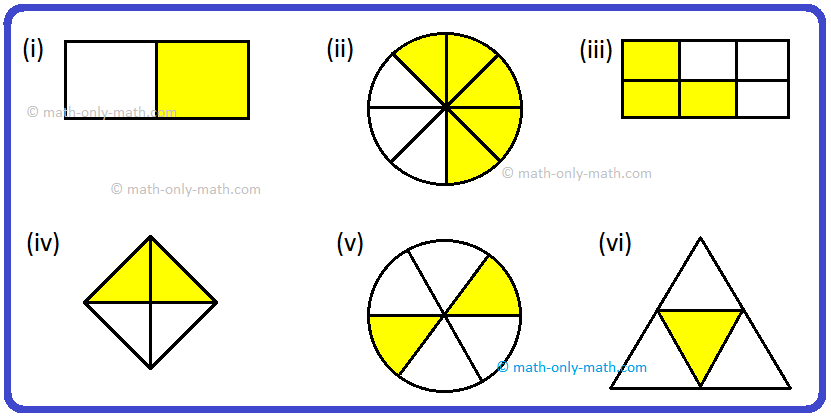
7. Give the fraction of the colored figure and convert in the lowest form.
|
Figure |
Fraction |
Lowest Form | |
|
(i) |
 | ||
|
(ii) |
 | ||
|
(iii) |
 | ||
|
(iv) |
 |
7.
Answers:
|
Figure |
Fraction |
Lowest Form | |
|
(i) |
 |
28 |
14 |
|
(ii) |
 |
48 |
12 |
|
(iii) |
 |
612 |
12 |
|
(iv) |
 |
26 |
13 |
8. Simplify the following fractions:
(i) 7580
(ii) 1220
(iii) 2545
(iv) 1824
(v) 125500
Answer:
8. (i) 1516
(ii) 35
(iii) 59
(iv) 34
(v) 14
9. State whether the fraction is in its lowest terms or not:
(i) 1220
(ii) 89
(iii) 2029
(iv) 58
(v) 3857
(vi) 3338
(vii) 7095
(viii) 1827
Answer:
9. (i) No
(ii) Yes
(iii) Yes
(iv) Yes
(v) No
(vi) Yes
(vii) No
(viii) No
10. Reduce to the lowest terms:
(i) 1020
(ii) 2135
(iii) 3642
(iv) 4560
(v) 3654
(vi) 2849
Answer:
10. (i) 12
(ii) 35
(iii) 67
(iv) 34
(v) 23
(vi) 47
● Fractions
Addition and Subtraction of Fractions
● Fractions - Worksheets
Worksheet on Multiplication of Fractions
Worksheet on Division of Fractions
From Fraction in Lowest Terms to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
How to Do Long Division? | Method | Steps | Examples | Worksheets |Ans
Apr 22, 25 12:42 PM
As we know that the division is to distribute a given value or quantity into groups having equal values. In long division, values at the individual place (Thousands, Hundreds, Tens, Ones) are dividend… -
Division of Four-Digit by a One-Digit Numbers | Worksheet with Answer
Apr 22, 25 12:12 PM
In division of four-digit by a one-digit numbers are discussed here step by step. How to divide 4-digit numbers by single-digit numbers? -
Skip Counting by 10's | Concept on Skip Counting |Skip Counting by Ten
Apr 22, 25 11:53 AM
The concept on skip counting by 10’s or tens is an essential skill to learn when making the jump from counting to basic addition. The sequence chart will help us to write the number to complete the se… -
Worksheets on Missing Numbers from 1 to 25 | Missing Number Worksheets
Apr 22, 25 11:28 AM
Printable worksheets on missing numbers from 1 to 25 help the kids to practice counting of the numbers. -
Conversion of a Decimal Fraction into a Fractional Number | Decimals
Apr 22, 25 02:52 AM
We will discuss here about the working rule for the conversion of a decimal fraction into a fractional number. The rules of converting decimal number to fraction are


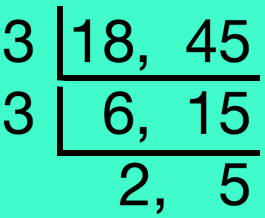

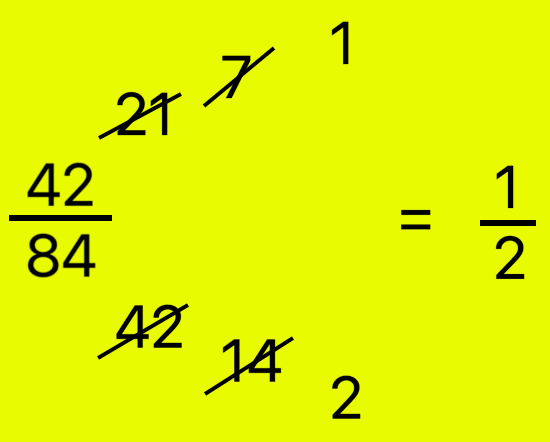














New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.