Equivalent Ratios

Learn about equivalent ratios to get the clear concept on ratio. We know that we use ratios to compare numbers.

How do we find two equivalent ratios by using multiplication and division?

To get a ratio equivalent to a given ratio we multiply or divide both the terms of the given ratio by the same non-zero number. We will learn how to find the equivalent ratios of a given ratio by writing the ratio as a fraction and then compare by using multiplication and division.

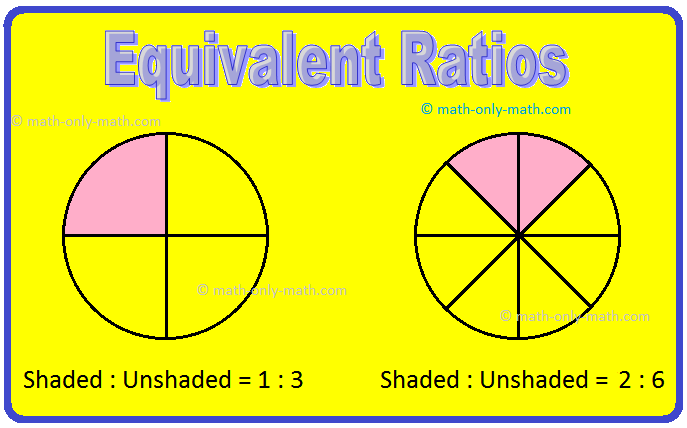
Look at the following figures

Also, 2 : 6 = $\frac{2}{6}$ = $\frac{1}{3}$ = 1 : 3

Hence, 1 : 3 and 2 : 6 are same ratio.

These are called equivalent ratios.

Solved Examples to Find Two Equivalent Ratios:

1. Give two equivalent ratios of 8 : 18.

Solution:

We will find the first equivalent ratio of 8 : 18 by using multiplication.

So, first we need to write the given ratio as fraction,

= $\frac{8}{18}$

= $\frac{8 × 2}{18 × 2}$

= $\frac{16}{36}$

= 16 : 36 (one equivalent ratio),

So, 16 : 36 is an equivalent ratio of 8 : 18.

Now we will find another equivalent ratio of 8 : 18 by using division.

Similarly, first we need to write the given ratio as fraction,

= $\frac{8}{18}$

= $\frac{8 ÷ 2}{18 ÷ 2}$

= $\frac{4}{9}$

= 4 : 9 (another equivalent ratio)

So, 4 : 9 is an equivalent ratio of 8 : 18.

Therefore, the two equivalent ratios of 8 : 18 are 16 : 36 and 4 : 9.

2. Frame two equivalent ratios of 4 : 5.

Solution:

To find two equivalent ratios of 4 : 5 we need to apply multiplication method only to get the answer in integer form.

First we need to write the given ratio as fraction,

= $\frac{4}{5}$

= $\frac{4 × 2}{5 × 2}$

= $\frac{8}{10}$

= 8 : 10 is one equivalent ratio,

Similarly again, we need to write the given ratio 4 : 5 as fraction to get another equivalent ratio;

= $\frac{4}{5}$

= $\frac{4 × 3}{5 × 3}$

= $\frac{12}{15}$ is another equivalent ratio

Therefore, the two equivalent ratios of 4 : 5 are 8 : 10 and 12 : 15.

Note: In this question we can’t apply division method to get the answer in integer form because the G.C.F. of 4 and 5 is 1. That means, 4 and 5 cannot be divisible by any other number except 1.

3. For the following ratio find the two equivalent ratios of 11 : 13.

Solution:

To find two equivalent ratios of 11 : 13 first we need to write the given ratio as fraction,

$\frac{11}{13}$

= $\frac{11 × 2}{13 × 2}$

= $\frac{22}{26}$

= 22 : 26 is one equivalent ratio

Similarly again, to get another equivalent ratio of 11 : 13;

$\frac{11}{13}$

= $\frac{11 × 4}{13 × 4}$

= $\frac{44}{52}$

= 44 : 52 is another equivalent ratio

Therefore, the two equivalent ratios of 11 : 13 are 22 : 26 and 44 : 52.

Note: If a : b and x : y are two equivalent ratios, we write $\frac{a}{b}$ = $\frac{x}{y}$.

Solved Examples to Find Three Equivalent Ratios:

1. Find three equivalent ratios of 3 : 8.

Solution:

3 : 8 = $\frac{3}{8}$ = $\frac{3 × 2}{8 × 2}$, [Multiply both numerator and denominator by 2]

= $\frac{6}{16}$

= 6 : 16 is the first equivalent ratio.

3 : 8 = $\frac{3}{8}$ = $\frac{3 × 4}{8 × 4}$, [Multiply both numerator and denominator by 4]

= $\frac{12}{32}$

= 12 : 32 is the second equivalent ratio.

3 : 8 = $\frac{3}{8}$ = $\frac{3 × 6}{8 × 6}$, [Multiply both numerator and denominator by 6]

= $\frac{18}{48}$

= 18 : 48 is the third equivalent ratio.

Therefore, the three equivalent ratios of 3 : 8 are 6 : 16, 12 : 32 and 18 : 48.

2. Find any three equivalent ratios of 3 : 2.

Solution:

3 : 2 = $\frac{3}{2}$ = $\frac{3 × 2}{2 × 2}$ = $\frac{6}{4}$ = 6 : 4

3 : 2 = $\frac{3}{2}$ = $\frac{3 × 3}{2 × 3}$ = $\frac{9}{6}$ = 9 : 6

3 : 2 = $\frac{3}{2}$ = $\frac{3 × 4}{2 × 4}$ = $\frac{12}{8}$ = 12 : 8

Hence, 6 : 4,  9 : 6 and 12 : 8 are three equivalent ratios of 3 : 2.

Worksheet on Equivalent Ratios:

1. Find two equivalent ratios of:

(i) 1 : 2

(ii) 5 : 3

(iii) 2 : 7

(iv) 3 : 8

Answer:

1. Find two equivalent ratios of:

(i) 2 : 4;   3 : 6

(ii) 10 : 6;   15 : 9

(iii) 4 : 14;   6 : 21

(iv) 6 : 16;   9 : 24

2. Fill in the blanks:

(i) $\frac{3}{7}$ = $\frac{9}{⯀}$

(ii) 2 : 3 = 8 : ⯀

(iii) $\frac{2}{5}$ = $\frac{⯀}{30}$

Answer:

2. (i) 21

(ii) 12

(iii) 12

6th Grade Page

From Equivalent Ratios to HOME PAGE