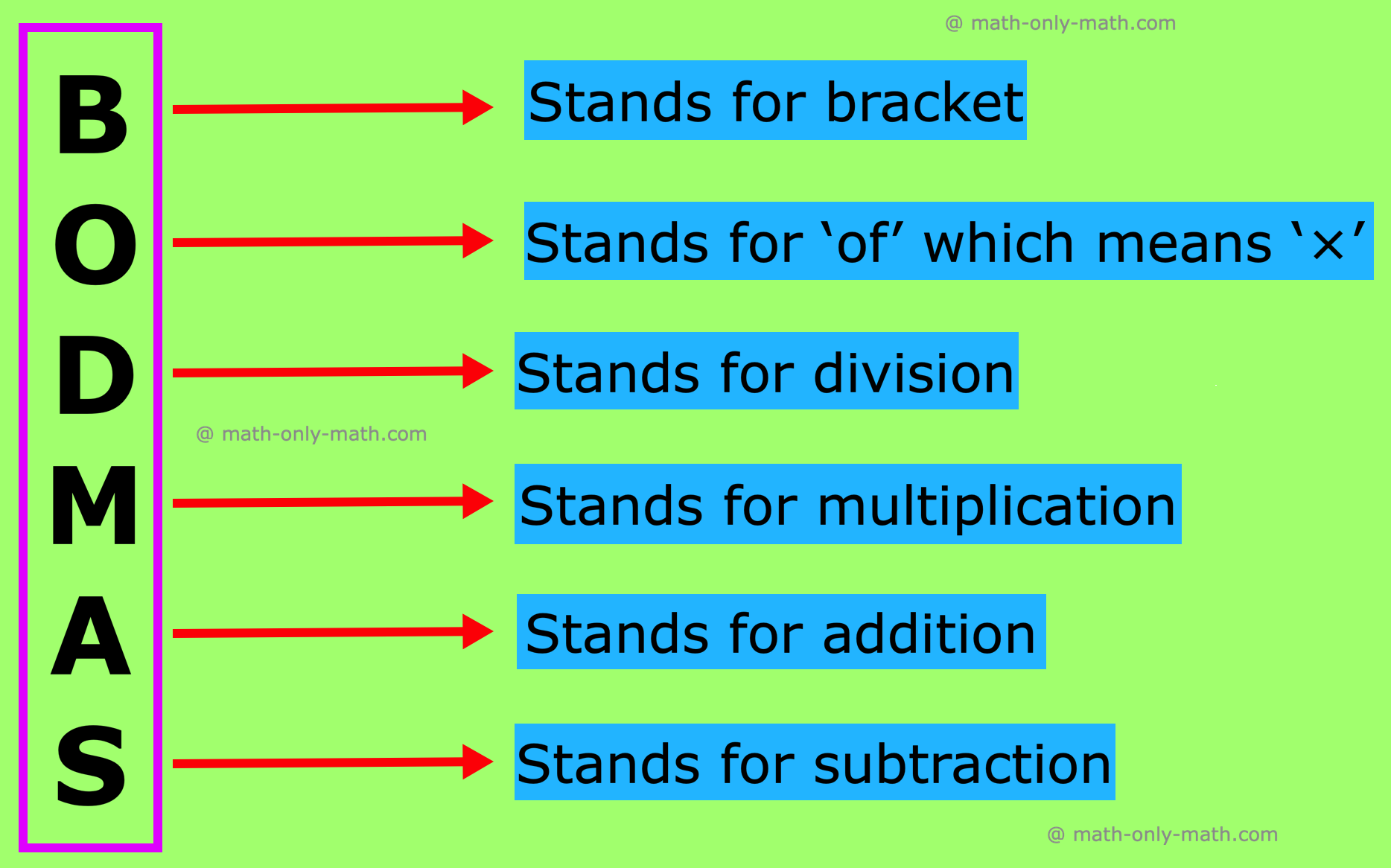
What is BODMAS Rule in Math?
Easy and simple way to remember BODMAS rule!!
B → Brackets first (parentheses)
O → Of (orders i.e. Powers and Square Roots, Cube Roots, etc.)
DM → Division and Multiplication (start from left to right)
AS → Addition and Subtraction (start from left to right)
Note:
(i) Start Divide/Multiply from left side to right side since they perform equally.
(ii) Start Add/Subtract from left side to right side since they perform equally.
Steps to simplify the order of operation using BODMAS rule:
First part of an equation is start solving inside the 'Brackets'.
For Example; (6 + 4) × 5
First solve inside ‘brackets’ 6 + 4 = 10, then 10 × 5 = 50.
Next solve the mathematical 'Of'.
For
Example; 3 of 4 + 9
First solve ‘of’ 3 × 4 = 12, then 12 + 9 = 21.
Next, the part of the equation is to calculate 'Division' and 'Multiplication'.
We know that, when division and multiplication follow one another, then their order in that part of the equation is solved from left side to right side.
For Example; 15 ÷ 3 × 1 ÷ 5
‘Multiplication’ and ‘Division’ perform equally, so calculate from left to right side. First solve 15 ÷ 3 = 5, then 5 × 1 = 5, then 5 ÷ 5 = 1.
In the last part of the equation is to calculate 'Addition' and 'Subtraction'. We know that, when addition and subtraction follow one another, then their order in that part of the equation is solved from left side to right side.
For Example; 7 + 19 - 11 + 13
‘Addition’ and ‘Subtraction’ perform equally, so calculate from left to right side. First solve 7 + 19 = 26, then 26 - 11 = 15 and then 15 + 13 = 28.
These are simple rules need to be followed for simplifying or calculating using BODMAS rule.
In brief, after we perform "B" and "O", start from left side to right side by solving any "D" or "M" as we find them. Then start from left side to right side solving any "A" or "S" as we find them.
MATHEMATICAL EXPRESSIONS INVOLVING DIFFERENT OPERATIONS
You have already learned about different operations such as addition, subtraction multiplication and division. Some mathematical expressions involve various operations.
For example, 9 - 12 ÷ 4 × 2 + 3
To simplify such a mathematical expression, we need to perform different operations in a certain order.
We perform the operations in the following order.
1. Division → 2. Multiplication → 3. Addition → 4. Subtraction
9 - 12 ÷ 4 × 2 + 3; [First, do division i.e. 12 ÷ 4 = 3]
= 9 - 3 × 2 + 3; [Now, do multiplication ie. 3 × 2 = 6]
= 9 - 6 + 3; [Now, do addition i.e. 9 + 3 = 12]
= 9 + 3 - 6; [As you have learned in your previous classes that the number having no sign is treated with '+' sign. So, we are adding here 9 with 3 instead of 6 with 3.]
= 12 - 6 [Finally, subtraction i.e. 12 - 6 = 6]
= 6
Note:
When we simplify a mathematical expression involving different operations, we follow the following order.
|
Division |
→ |
Multiplication |
→ |
Addition |
→ |
Subtraction |
|
÷ |
× |
+ |
- |
In short, we can remember DMAS where D, M, A and S are used for division, multiplication, addition and subtraction respectively.
Let us consider some examples.
1. Simplify the following.
(i) 24 - 4 + 6
(ii) 20 - 15 + 7
(iii) - 9 + 20 - 3
(iv) 28 + 15 - 19
(v) 45 - 19 + 12
(vi) - 39 + 56 - 2
Solution:
These mathematical expressions involve only addition and subtraction operations. We have already learnt that if we have to addition and subtraction both together first do the addition of numbers with '+' sign then do subtraction '-'.
Let's, start from addition.
(i) 24 - 4 + 6
= 24 + 5 - 4
= 29 - 4; [Addition]
= 25; [Subtraction]
Therefore, 24 - 4 + 5 = 25
(ii) 20 - 15 + 7
= 20 + 7 - 15
= 27 - 15; [Addition]
= 12; [Subtraction]
Therefore, 20 - 15 + 7 = 12
(iii) - 9 + 20 - 3
= 20 - 9 - 3
= 20 - 12
= 8; [Subtraction]
Therefore, - 9 + 20 - 3 = 8
(iv) 28 + 15 - 19
= 43 - 19; [Addition]
= 24; [Subtraction]
Therefore, 28 + 15 - 19 = 24
(v) 45 - 19 + 12
= 45 + 12 - 19
= 57 - 19; [Addition]
= 38; [Subtraction]
Therefore, 45 - 19 + 12 = 38
(vi) - 39 + 56 - 2
= 56 - 39 - 2
= 56 - 41
= 15; [Subtraction]
Therefore, - 39 + 56 - 2 = 15
2. Simplify the following.
(i) 25 - 2 × 3 + 9
(ii) 6 × 8 - 10 ÷ 5 + 4
(iii) 28 ÷ 14 × 2 + 35 - 2
(iv) 56 × 4 + 3 × 12 ÷ 4 - 7
Solution:
(i) 25 - 2 × 3 + 9
This mathematical operation is having no division. So, we start from multiplication.
25 - 2 × 3 + 9; [Multiplication 2 × 3]
= 25 - 6 + 9; [Now, add the numbers with '+' sign]
= 25 + 9 - 6; [Addition 25 + 9 = 34]
= 34 - 6; [Subtraction 34 - 6 = 28]
= 28
Therefore, 25 - 2 × 3 + 9 = 28
(ii) 6 × 8 - 10 ÷ 5 + 4; [Divide 10 ÷ 5 = 2]
= 6 × 8 - 2 + 4; [Multiply 6 × 8 = 48]
= 48 + 4 - 2; [Add 48 + 4 = 52]
= 52 - 2; [Subtract 52 - 2 = 50]
= 50
Therefore, 6 × 8 - 10 ÷ 5 + 4 = 50
(iii) 28 ÷ 14 × 2 + 35 - 2; [Divide 28 ÷ 14 = 2]
= 2 × 2 + 35 - 2; [Multiply 2 × 2 = 4]
=4 + 35 - 2; [Add 4 + 35 =39]
= 39 - 2; [Subtract 39 - 2 = 37]
= 37
Therefore, 28 ÷ 14 × 2 + 35 - 2 = 37
(iv) 56 × 4 + 3 × 12 ÷ 4 - 7; [Divide 12 ÷ 4 = 3]
= 56 × 4 + 3 × 3 - 7; [Multiply 3 × 3 = 9 and 56 × 4 = 224]
= 224 + 9 - 7; [Add 224+9 = 233]
=233 - 7; [Subtract 233 - 7 = 226]
= 226
Therefore, 56 × 4 + 3 × 12 ÷ 4 - 7 = 226
MATHEMATICAL EXPRESSIONS WITH 'BRACKETS' AND 'OF'
So far we have considered mathematical expressions involving operations such as addition, subtraction, multiplication and division only.
Now we will consider some different mathematical expressions with 'brackets' and 'of' also along with other operations.
Let us consider the following mathematical expression
6[425 - {66 ÷ (9 - 3)}] - 2
This expression has square brackets [ ], curly brackets { }, simple brackets ( ), and 'of' also apart from other mathematical operations.
While simplifying such a mathematical expression, we perform the operations in the following order.
1. We remove brackets in the following order:
a. Simple brackets First bracket or Parenthesis or '( )'
b. Curly brackets or Second bracket '{ }'
c. Square brackets or Third bracket '[ ]'
2. 'of' (Remember, 'of means multiplication)
3. Division
4. Multiplication
5. Addition
6. Subtraction
In short, we can remember BODMAS to solve such mathematical expressions Here,
Consider the above expression.
6[425 - {66 ÷ (9 - 3)}] - 2
First we remove the brackets.
6[425 - {66 ÷ (9 - 3)}] - 2; First remove ( ) bracket
= 6[425 - {66 ÷ 6}] - 2; Remove { } bracket
= 6[425 - 11] - 2;
= 6[414] - 2; Remove [ ] bracket
= 2484 - 2
= 2482
Therefore, 6[425 - {66 ÷ (9 - 3)}] - 2 = 2482
Note: When a number written outside of a bracket without any sign. It means we have to multiply the number with the solution of expression of that bracket.
Some mathematical expressions may have '______' also called a line bracket, above a group of numbers. In such cases, we remove this line bracket first.
We can understand the method of simplification of such mathematical expressions more clearly with the help of the following examples.
1. Simplify the following mathematical expression using BODMAS rule:
521 of [4 + {4 (15 + ¯9−4)}] - 3
Solution:
521 of [4 + {4 (15 + ¯9−4)}] - 3
= 521 of [4 + {4 (15 + 5)}] - 3; Removal of '______'
= 521 of [4 + {4 × 20)}] - 3; Removal of '( )'
= 521 of [4 + 80] - 3; Removal of '{ }'
= 521 of 84 - 3; Removal of '[ ]'
= 521 × 84 - 3; Removal of 'of'
= 521 × 841 - 3; Multiplication
= 5×8421×1 - 3
= 42021 - 3
= 20 - 3; Since 42021 = 20
= 17; Subtraction.
Therefore, 521 of [4 + {4 (15 + ¯9−4)}] - 3 = 17
2. Simplify the following mathematical expression using BODMAS rule:
38 of [8 + {3 (12 - ¯7−3)}] × 3
Solution:
38 of [8 + {3 (12 - ¯7−3)}] × 3
= 38 of [8 + {3 (12 - 4)}] × 3; Removal of '______'
= 38 of [8 + {3 × 8}] × 3; Removal of '( )'
= 38 of [8 + 24] × 3; Removal of '{ }'
= 38 of 32 × 3; Removal of '[ ]'
= 38 × 32 × 3; Removal of 'of'
= 38 × 321 × 31; Multiplication
= 3×32×38×1×1
= 2888
= 36; Since 2888 = 36
Therefore, 38 of [8 + {3 (12 - ¯7−3)}] × 3 = 36
Worksheet on Simplification using BODMAS Rule
I. Simplify the following using basic four mathematical operations:
1. 54 - 3 + 4 + 9 ÷ 3
2. 62 - 24 ÷ 8 × 3 + 6
3. 28 - 2 × 5 ÷ 2 + 24 - 17
4. 48 ÷ 8 + 24 - 3 × 2
5. 64 + 8 ÷ 4 × 6 - 27
6. 55 - 3 × 6 ÷ 9 + 3
7. 14 × 5 - 72 ÷ 12 - 8 + 12
8. 25 × 5 ÷ 25 - 2 + 3
9. 17 × 4 - 27 ÷ 9 + 25
10. 8 × 8 ÷ 4 - 2 + 6
Answer:
I. 1. 58
2. 59
3. 30
4. 24
5. 59
6. 56
7. 68
8. 6
9. 90
10. 20
II. Simplify the fractions using basic four mathematical operations:
1. 102 × 4 - 7 × 4 ÷ 23
2. 23 + 56 ÷ 16 - 19 × 2
3. 225 × 49 ÷ 47 + 35 - 25
4. 214 × 8 - 18 × 14 + 23
5. 623 + 4512 ÷ 712 - 512
6. 423 × 23 - 13 + 123 ÷ 13
7. 214 × 135 + 234 ÷ 14 - 134
8. 517 + 4114 ÷ 27 × 221 - 17
9. 416 × 2338 - 27 + 56 ÷ 16
10. 1723 × 112 ÷ 37 - 27 + 113
Answer:
II. 1. 366
2. 549
3. 2115
4. 161112
5. 132328
6. 779
7. 121720
8. 6514
9. 36011596
10. 623742
III. Simplify the following mathematical expressions using BODMAS rule:
1. 12 × {20 - (12 - 7)}
2. 28 × {21 + (29 - 12)}
3. 34 × (68 - (32 - 12)}
4. 96 × {30 - (18 + 10)}
5. 24 × {18 - (15 - 10)}
6. 21 × {24 + (30 - 24)}
7. 75 × {25 + (54 - 17)}
8. 54 [21 - {2 + (30 - 14)}]
9. (13 - 14) ÷ 123 × 4 + 212
10. 900 ÷ (36 × 5) - 15 ÷ 3
Answer:
III. Simplify the following mathematical expressions using BODMAS rule:
1. 180
2. 1064
3. 1632
4. 192
5. 312
6. 630
7. 4650
8. 162
9. 2(710
10. 0
● Related Concept
● Decimals
● Conversion of Unlike Decimals to Like Decimals
● Decimal and Fractional Expansion
● Converting Decimals to Fractions
● Converting Fractions to Decimals
● H.C.F. and L.C.M. of Decimals
● Repeating or Recurring Decimal
● BODMAS/PEMDAS Rules - Involving Decimals
● PEMDAS Rules - Involving Integers
● PEMDAS Rules - Involving Decimals
● BODMAS Rules - Involving Integers
● Conversion of Pure Recurring Decimal into Vulgar Fraction
● Conversion of Mixed Recurring Decimals into Vulgar Fractions
● Rounding Decimals to the Nearest Whole Number
● Rounding Decimals to the Nearest Tenths
● Rounding Decimals to the Nearest Hundredths
● Simplify Decimals Involving Addition and Subtraction Decimals
● Multiplying Decimal by a Decimal Number
● Multiplying Decimal by a Whole Number
● Dividing Decimal by a Whole Number
● Dividing Decimal by a Decimal Number
7th Grade Math Problems
From BODMAS Rule to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
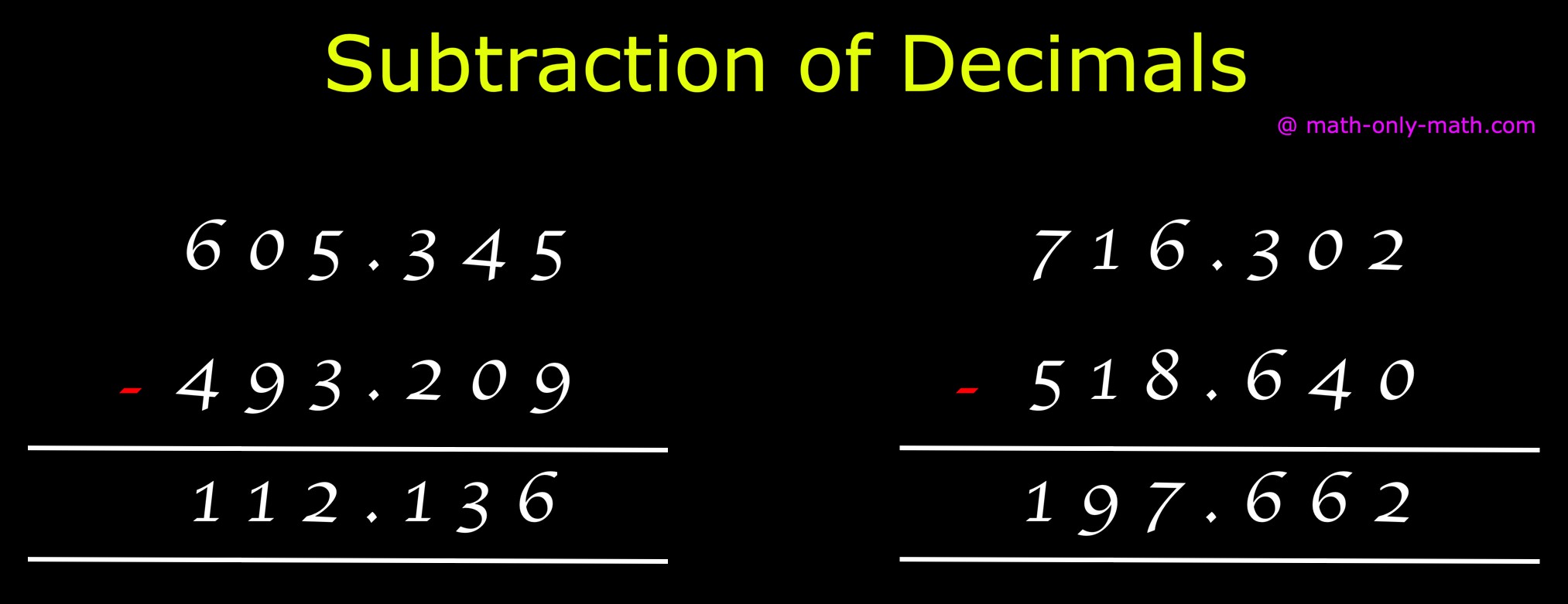
Subtraction of Decimals | Subtracting Decimals | Decimal Subtraction
Apr 24, 25 03:25 PM
We will discuss here about the subtraction of decimals. Decimals are subtracted in the same way as we subtract ordinary numbers. We arrange the digits in columns -
How to Do Long Division? | Method | Steps | Examples | Worksheets |Ans
Apr 24, 25 10:18 AM
As we know that the division is to distribute a given value or quantity into groups having equal values. In long division, values at the individual place (Thousands, Hundreds, Tens, Ones) are dividend… -
Division by Two-Digit Numbers | Knowledge of Estimation | Division
Apr 24, 25 10:12 AM
In division by two-digit numbers we will practice dividing two, three, four and five digits by two-digit numbers. Consider the following examples on division by two-digit numbers: Let us use our knowl… -
Addition of Decimals | How to Add Decimals? | Adding Decimals|Addition
Apr 24, 25 01:45 AM
We will discuss here about the addition of decimals. Decimals are added in the same way as we add ordinary numbers. We arrange the digits in columns and then add as required. Let us consider some -
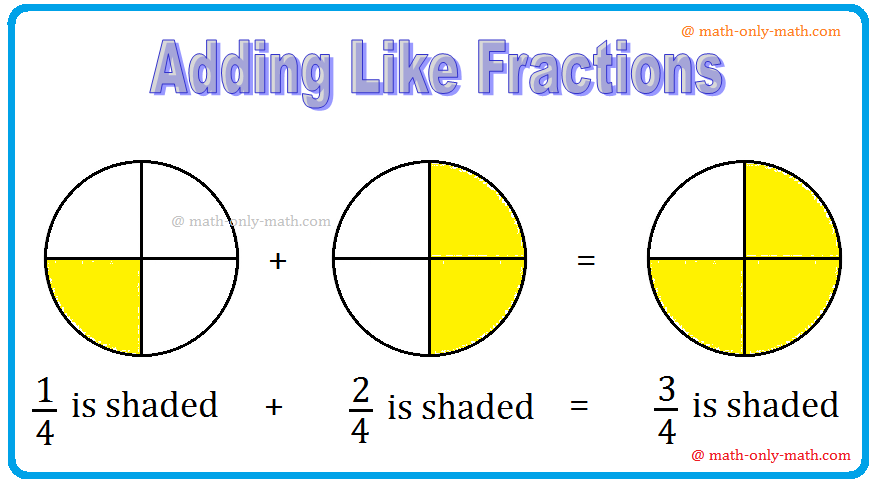
Addition of Like Fractions | Examples | Videos | Worksheet | Fractions
Apr 23, 25 09:23 AM
To add two or more like fractions we simplify add their numerators. The denominator remains same. Thus, to add the fractions with the same denominator, we simply add their numerators and write the com…




New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.