Perimeter and Area of Plane Figures

We are already familiar with various shapes like square, rectangle, triangle, parallelogram, circle, etc. Now we will further study about these shapes in terms of measurement. Here, we will learn about area and perimeter of closed figures that are both regular and irregular. Perimeter refers to the boundary of a flat shape and area refers to the space occupied or enclosed by the boundary. Circumferences is the special kind of perimeter that means distance around a circle.

A plane figure is made of line segments or arcs of curves in a plane. It is a closed figure if the figure begins and ends at the same point. We are familiar with plane figures like squares, rectangles, triangles and circles.

I. Perimeter of Plane Figures:

Definition of Perimeter:

The perimeter (P) of a closed plane figure is the sum of the lengths of its bounding sides (line segments or arcs). Perimeter is measured in units of length such as centimetre (cm) and metre (m).

Thus, perimeter of a closed figure is the total lengths of its boundary.

We know that all polygons (triangle, square, rectangle, pentagon, hexagon, etc.) are rectilinear figures.

Perimeter = Sum of the lengths of all its sides.

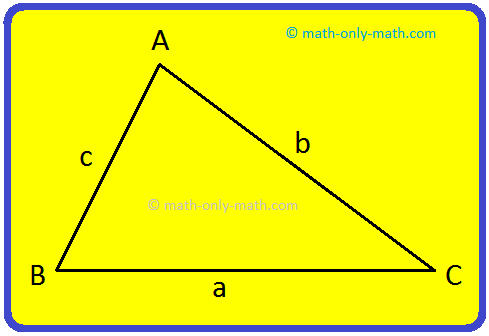
Perimeter of a Triangle:

The perimeter of a triangle ABC, is the sum of the lengths of its sides. If the lengths of the sides of a triangle are a, b, and c, then

Perimeter = AB + BC + CA

              = c + a + b

              = a + b + c

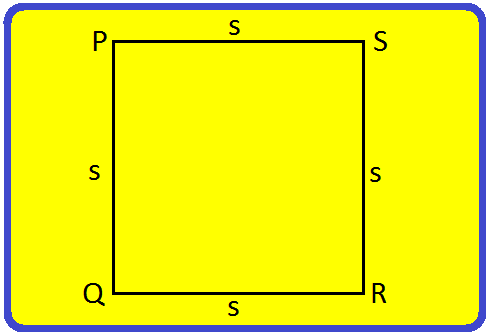
Perimeter of a Square:

The perimeter of a square PQRS is the total length of all its equal sides. If the length of each side is s then,

Perimeter = PQ + QR + RS + SP

               = 5 + 5 + 5 + 5

               = 4s

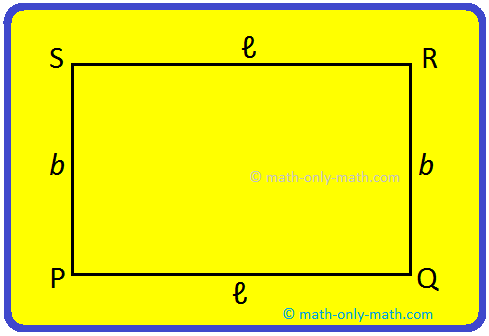
Perimeter of a Rectangle:

The perimeter of a rectangle PQRS is the double of the sum of its two adjacent sides. If the lengths of its two adjacent sides are ℓ and b, then,

Perimeter = PQ + QR + RS + SP

               = ℓ + b + ℓ + b

               = 2ℓ + 2b

               = 2 (ℓ + b)

Note:

Perimeter is the distance along the side of a closed figure.

Distance is found out by adding all the sides of the closed figure.

It is measured in metre, decimeter, centimeter, decameter, etc.

Shapes of Different Kinds with the Same Perimeter:

We can have different kinds of shapes with the same perimeter. To understand this, let us take a string 32 cm long. What figures can we make by using his string?

We can make an isosceles triangle of side 10 cm, 10 cm, and 12 cm.

Perimeter = PQ + QR + PR

              = 10 cm + 12 cm + 10 cm

              = 32 cm

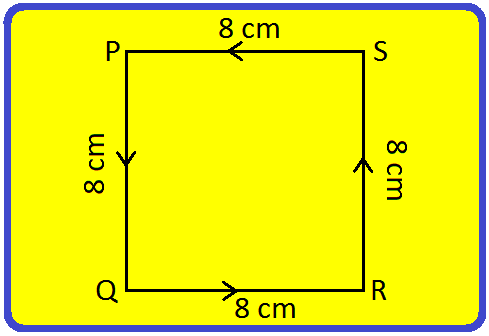
By using a 32 cm string, we can make a square of side 8 cm.

Perimeter = PQ + QR + RS + PS

               = 8 cm + 8 cm + 8 cm + 8 cm + 8 cm

               = 4 × 8 cm

               = 32 cm

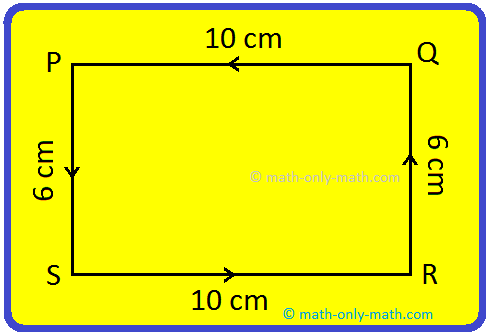
By using the same string, we can make a rectangle of length 10 cm and breadth 6 cm.

Perimeter = PQ + QR + RS + PS

               = 6 cm + 10 cm + 6 cm + 10 cm

               = 32 cm

We see that in all the three cases, the perimeter is 32 cm but they have different shapes. Hence, we can conclude that different kinds of shapes can have the same perimeter.

Note: Two lengths of different units cannot be added, For adding we shall have to convert them into the same unit.

Solved Examples on Perimeter of Plane Figures:

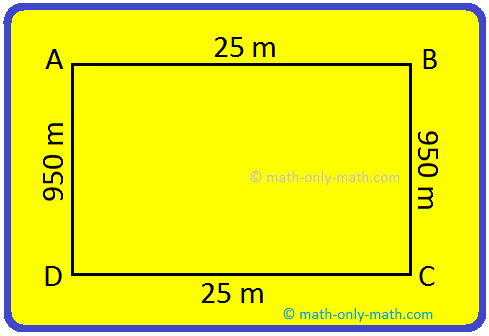
1. Find the perimeter of a rectangular plot whose length is 25 m and breadth is 950 cm.

Solution:

Length of the rectangle = 25 m

Breadth of the rectangle = 950 cm

                                    = \(\frac{950}{100}\) m; [Since, 1 m = 100 cm)

                                   = 9.5 m

Perimeter of the rectangular plot = 2 (Length + Breadth)

                                                = 2 (ℓ + b)

                                                = 2 (25 + 9.5)

                                                = 2 × 34.5

                                                = 69 m

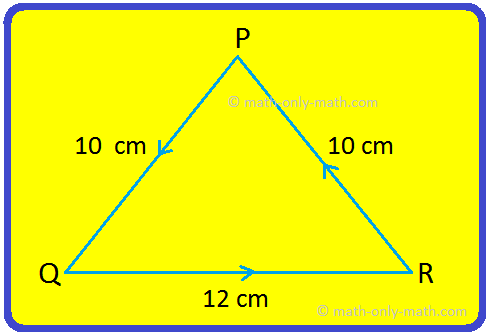
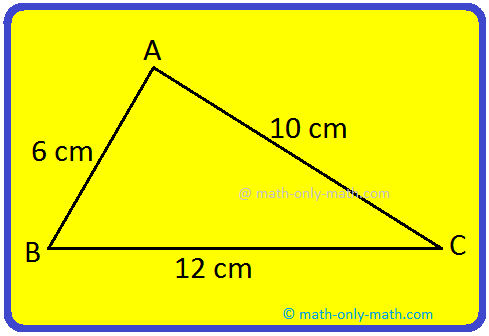
2. Find the length of a string used to make a triangle ABC. If the same string is used to make a square, what will be the side of the square?

Solution:

Perimeter of ABC = Length of the string

                          = AB + BC + CA

                          = 6 cm + 12 cm + 10 cm

                          = 28 cm

Now, the same string is used to make a square. So the perimeter of a square will be 28 cm.

Perimeter of a square = 4 x side

                  ⟹ 28 cm = 4 x side

                  ⟹ 4 x side = 28 cm

                  ⟹ side = \(\frac{28}{4}\) cm = 7 cm

Hence, the side of a square will be 7 cm.

I. Area of Plane Figures:

The area of the portion of the plane or shape can be defined as the amount of stuff required to cover it. For finding the area of a polygon, we consider the enclosed region of the polygon.

Let us consider an illustration to clarify the idea.
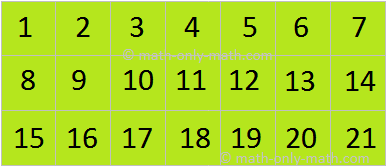
A news bulletin board in a class is to be covered with squared colour paper sheets. To know how many colour paper sheets are required for the said purpose, the best way is to lay the board on the floor and cover it with a coloured paper sheet without any gap as shown in the figure.

Count the number of sheets used for this purpose. Suppose 21 sheets are used to cover the complete board, then, we can measure the region enclosed by a polygon. This measurement called the area of the polygon.

Therefore, Area = 21 × Area of 1 sheet

The amount of surface enclosed by a plane figure is called its area. It is measured in square units of lengths.

Note:

Area of a square of side 1 cm is 1 cm², because when we multiply the lengths of two sides, we also multiply their units as cm × cm, i.e., equal to cm². The standard unit of area is cm².

Definition of Area:

The area (A) of a closed plane figure is the region of the plane enclosed by the figure’s boundary. Area is measured in square units of length such as square centimetre (cm\(^{2}\)) and square metre (m\(^{2}\)).

To Find the Area of a Figure using a Graph:

We can find the area of regular and irregular figures by using a graph or squared paper. To find the area, first we draw the figure on the graph paper covering as many squares as possible.

For finding the area by using squared paper, we have to follow the following steps:

(i) Count the number of complete square of units length enclosed by the figure.

(ii) Count the number of those square whose more than half parts are enclosed by the figure.

(iii) Count the number of those square whose exact half parts are enclosed by the figure and divide the number by 2.

(iv) Leave those square whose less than half parts are enclosed by the figure.

(v) The total of steps (i), (ii) and (iii) are added to obtain the area of the figure.

Therefore, Area of the figure = Number of complete square + Number of squares having more than half parts enclosed + \(\frac{1}{2}\) (Number of squares having half parts enclosed)

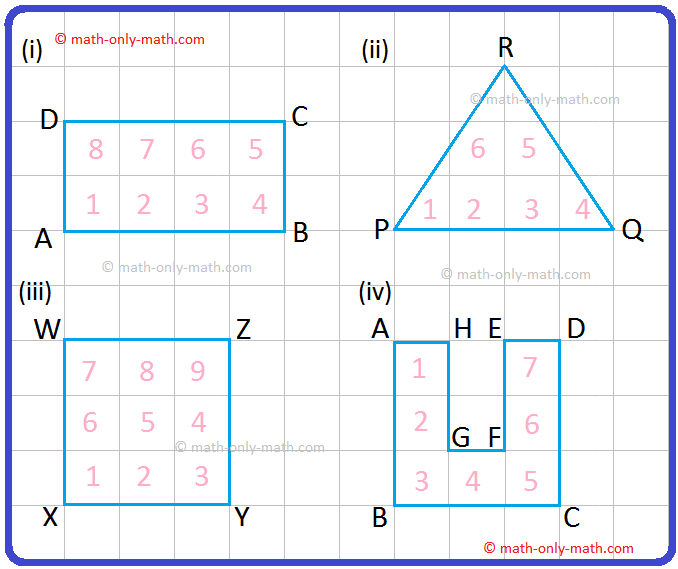
1. Area of rectangular ∆BCD

               = 8 × Area of one square

               = 8 × 1 cm²

               = 8 cm²

Thus, if the length and breadth of a rectangle are 4 cm and 2 cm, respectively, then

                Area = 8 cm² = (4 × 2) sq. cm

Therefore, Area = length × breadth

2. Area of ∆PQR = Number of complete squares + Number of squares having more than half parts + \(\frac{1}{2}\) × Number of halved squares.

Number of squares enclosed in the figure = 2

Number of squares whose more than half parts are enclosed = 4

Neglect the number of squares whose less than half part is enclosed.

Area of ∆PQR = 2 + 4 + \(\frac{1}{2}\) × 0

                    = 6 squares

                    = 6 × 1 cm²

                    = 6 cm²

Thus, if the base and height of the triangle are 4 cm and 3 cm, respectively, then

           Area = 6 cm²

                  = \(\frac{1}{2}\) × (4 × 3)

                  = \(\frac{1}{2}\) × base × height

3. Area of square WXYZ

                   = 9 × Area of one square

                   = 9 × 1 cm²

                   = 9 cm²

Thus, if the side of the square is 3 cm, then

           Area = 9 cm²

                  = (3 × 3) cm²

                  = side × side

4. Similarly, area of figure ABCDEFGH

                 = 7 × Area of one square

                 = 7 × 1 cm²

                 = 7 cm²

Solved Example on Area of Plane Figures:

1. Find the area of a square whose side is 9 cm.

Solution: Area of square

                          = side × side

                          = 9 cm × 9 cm

                          = 81 cm²

2. Find the area of a rectangle whose length is 26 cm and breadth is 19 cm.

Solutions: Area of a rectangle

                           = length × breadth

                           = 26 cm × 19 cm

                           = 494 cm²

9th Grade Math

From Perimeter and Area of Plane Figures to HOME PAGE