Area of a Rectangle

Area of a rectangle is discussed here. We know, that a rectangle has length and breadth.

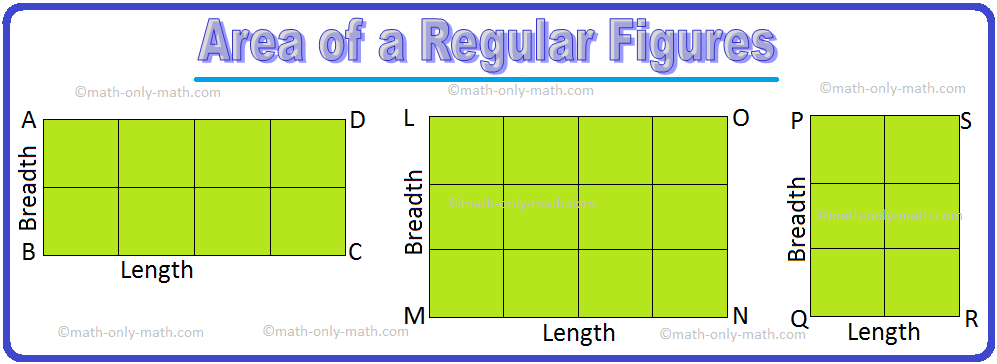
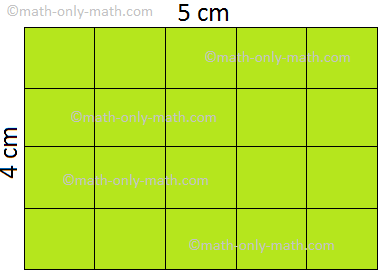
Let us look at the rectangle given below.

Each rectangle is made of squares. The side of each square is 1 cm long. The area of each square is 1 square centimeter.

The rectangle ABCD has 8 such squares. Therefore, its area is 8 sq cm. Similarly we can find the areas of the other rectangles by counting the number of squares. We also note the length and breadth of each rectangle and write in the table below:

In each case we observe the length × breadth = Area of the rectangle.

Therefore, area of rectangle = length × breadth = l × b sq. units

From the above multiplication, we get the following facts:

Length of the rectangle = \(\frac{\textrm{Area of the Rectangle}}{\textrm{Breadth of the Rectangle}}\)

Breadth of the rectangle = \(\frac{\textrm{Area of the Rectangle}}{\textrm{Length of the Rectangle}}\)

Consider the following rectangle PQRS of length PQ = 3 cm and breadth = QR = 5 cm.

Here the area of each smaller square is 1 sq.cm. There are 15 squares in PQRS. So, its area is sq. cm. In the given rectangle, there are 5 squares along the length PS and 3 squares along the breadth PQ. When we multiply 5 and 3, length and breadth of the rectangle PQRS, we get 15 which is the area of the rectangle PQRS.

Hence, area of a rectangle = length × breadth

                                    A = l × b

Where A is the area and l and b are length and breadth of a rectangle.

Consider the following figures:

(i)

Area of each small square = 1 sq cm

Area of rectangle in figure 1 by counting the squares = 6 sq. cm

Area = 6 square cm

Length of rectangle = 3 cm

Breadth of rectangle = 2 cm

Area = 3 × 2 = 6 sq. cm

(ii) 

Area of each small square = 1 sq cm

Area of rectangle in figure 2 by counting the squares = 10 sq. cm

Area = 10 square cm

Length of rectangle = 5 cm

Breadth of rectangle = 2 cm

Area = 5 × 2 = 10 sq. cm

Hence, area of rectangle = length × breadth

A = l × b where, A is the area, l and b are length and breadth of a rectangle.

Let us find the area of a rectangle having length 5 cm and breadth 4 cm.

From the above figure, it is clear that we can divide this rectangle into 20 squares of sides 1 cm each. So, the area = 20 cm²

Thus the area of the rectangle = 5 cm × 4 cm

                                             = 20 cm²

So when we multiply its length and breadth we get the area of the rectangle.

Solved examples to find the area of a rectangle when length and breadth are given:

1. Ron’s kitchen is 5 meter long and 3 meter broad. Find the area of the floor of the kitchen.

Solution:

Area = length × breadth

       = 5 × 3

       = 15 sq. m

2. Find the area of a rectangular park whose length and breadth are 25 m and 15 m respectively.

Solution:

Length of a rectangular park = 25 m

Breadth of a rectangular park = 15 m

Area of the park = length × breadth

                              = 25 m × 15 m

                              = 375 sq. m

3. Find the area of a rectangle of length 12 cm and breadth 3 cm.

Solution:

Length (l) of the rectangle = 12 cm.

Breadth (b) of the rectangle = 3 cm.

Area of the rectangle = length × breadth 

                               = 12 × 3 sq cm.

                               = 36 sq cm.

4. Find the area of a rectangle of length 15 cm and breadth 6 cm.

Solution:

Length of the rectangle = 15 cm.

Breadth of the rectangle = 6 cm.

Area of the rectangle = l × b

                               = 15 × 6 sq cm.

                               = 90 sq cm.

5. Robert wants to paint the front wall of his house. The wall is 3 m long and 2.5 m broad. If the cost of painting is $ 120 per square metre, find the cost of painting the wall.

Solution:

Length of the wall = 3 m

Breadth of the wall = 2.5 m

Area of the wall = 3 × 2.5 sq. m

                       = 7.5 sq. m

The cost for per square metre painting is $ 120.

Therefore, the cost for 7.5 sq. m painting is $7.5 × 120 = $ 900

6. Find the area of a rectangle of length 17 cm and breadth 9 cm.

Solution:

The length of the rectangle = 17 cm.

the breadth of the rectangle = 9 cm.

The Area of the rectangle = l × b

                                     = 17 × 9 sq cm.

                                     = 153 sq cm.

7. A tennis court is 24 m long and 8 m broad. Find its area.

Solution:

The length of the tennis court = 24 m

The breadth of the tennis court = 8 m

Therefore, the area of the tennis court = 24 × 8 sq m.

                                                        = 192 sq. m

8. Find the area of a rectangle of length 24 mm and breadth 8 mm.

Solution:

Length of the rectangle = 24 mm.

Breadth of the rectangle = 8 mm.

Area of the rectangle = l × b

                               = 24 × 8 sq mm.

                               = 192 sq mm.

9. Find the area of a rectangle of length 37 mm and breadth 19 mm.

Solution:

Length of the rectangle = 37 mm.

Breadth of the rectangle = 19 mm.

Area of the rectangle = l × b

                               = 37 × 19 sq mm.

                               = 703 sq mm.

10. Mike has a rectangular garden of length 15 m and breadth 10 m. Her friend Adam has a square garden of side 12 m. whose garden is bigger and by how much?

Solution:

Length of Mike’s garden = 15 m

Breadth of Mike’s garden = 10 m

Area of Mike’s garden = 15 × 10 sq. m = 150 sq m

Area of Adam’s garden = 12 × 12 = 144 sq. m

Hence, Mike’s garden is bigger.

11. Find the area of a rectangular cardboard 1 m long and 25 cm broad.

Solution:

Length is in meters but the breadth is in cm.

So, first we need to change the meters into cm.

We know that, 1 m = 100 cm

Thus, the area of the rectangular cardboard = ℓ × b

                                                                = 100 × 25 sq. cm

                                                                = 2,500 sq. cm

12. Length of a rectangular park is 6 times its breadth. If the length of the park is 42 meters, then find the area of the park.

Solution:

According to the problem, 

Length of a rectangular park is 6 times its breadth.

Length of rectangular park = 42 m.

So, the breadth of the rectangular park = (42 ÷ 6) m = 7 m

Area of the rectangle = length × breadth

                               = ℓ × b

                               = 42 m × 7 m

                               = 294 m²

Therefore, the area of the rectangular park = 294 m²

Worksheet on Area of a Rectangle:

1. Find the area of the given rectangles.

(i) Length = 4 cm, Breadth = 7 cm

(ii) Length = 15 cm, Breadth = 4 cm

(iii) Length = 4.2 m, Breadth = 50 cm

(iv) Length = 1 m 40 cm, Breadth = 5 m 50 cm

(v) Length = 65 mm, Breadth = 21 mm

Answers:

(i) 28 sq. cm

(ii) 60 sq. cm

(iii) 21,000 sq. cm

(iv) 7.7 sq. m

(v) 1365 sq. mm

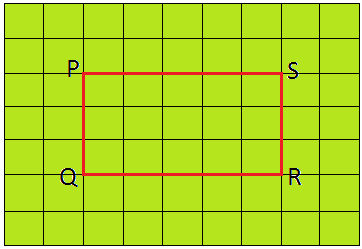
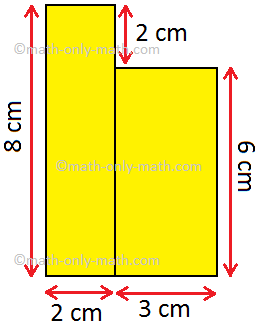
2. Find the area of the given figure.

Answer:

34 sq. cm

3. Find the area of the rectangle, whose length and breadth are respectively;

(i) 5 cm and 4 cm

(ii) 100 cm and 30 cm

(iii) 10 cm and 15 cm

(iv) 300 cm and 250 cm

(v) 22 m and 35 m

(vi) 25 m and 20 m

Answers:

(i) 20 sq. cm

(ii) 3000 sq. cm

(iii) 150 sq. cm

(iv) 75000 sq. cm

(v) 770 sq. m

(vi) 500 sq. m

Word Problems on Area of a Rectangle:

4. The area of one of the wall of the class 12 square m. If the length of the wall is 3 m. then what is the height of the wall?

Answer:

4 m

5. The perimeter of a rectangular tennis court is 70 m. If its length is 28 m, find its area.

Answer:

196 sq. m

● Area.

Area of a Rectangle.

Area of a Square.

To find Area of a Rectangle when Length and Breadth are of Different Units.

To find Length or Breadth when Area of a Rectangle is given.

Areas of Irregular Figures.

To find Cost of Painting or Tilling when Area and Cost per Unit is given.

To find the Number of Bricks or Tiles when Area of Path and Brick is given.

Worksheet on Area.

Worksheet on Area of a Square and Rectangle

Practice Test on Area.

5th Grade Geometry

5th Grade Math Problems

From Area of a Rectangle to HOME PAGE