Important Properties of Direct Common Tangents

We will discuss here three important properties of direct common tangents.

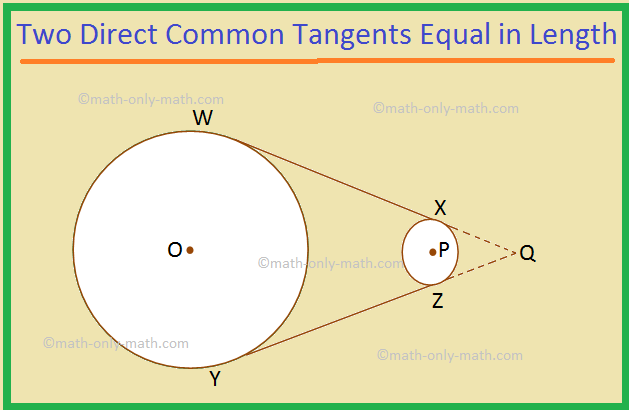
I. The two direct common tangents drawn to two circles are equal in length.

Given: WX and YZ are the two direct common tangents drawn to the two given circles with centres O and P.

To prove: WX = YZ.

Construction: Produce WX and YZ show that they meet at Q.

Proof:

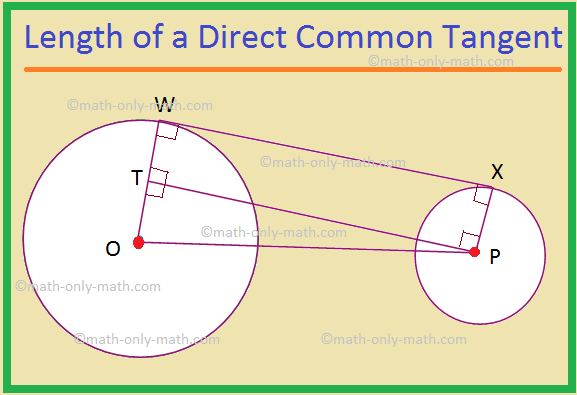
II. The length of a direct common tangent to two circles is \(\sqrt{d^{2} – (r_{1} – r_{2})^{2}}\), where d is the distance between the centres of the circles, and r\(_{1}\) and r\(_{2}\) are the radii of the given circles.

Proof:

Let two circles be given with centres O and P, and radii r\(_{1}\) and r\(_{2}\) respectively. Let WX be a direct common tangent.

Therefore, OW = r\(_{1}\) and PX = r\(_{2}\).

Also, r\(_{1}\) > r\(_{2}\).

Let the distance between the centres of the circles, OP = d.

Draw PT ⊥ OW.

Now, OW ⊥ WX and PX ⊥ WX, because a tangent is perpendicular to the radius drawn through the point of contact

Therefore, WXPT is a rectangle.

So, WT = XP = r\(_{2}\) and WX = PT, and the opposite sides of a rectangle are equal.

OT = OW – WT = r\(_{1}\) - r\(_{2}\).

In the right-angled triangle OPT,

We have, PT² = OP² – OT² [by, Pythagoras Theorem]

          ⟹ PT² = d² – (r\(_{1}\) - r\(_{2}\))\(^{2}\)

          ⟹ PT = \(\sqrt{d^{2} – (r_{1} – r_{2})^{2}}\)

          ⟹ WX = \(\sqrt{d^{2} – (r_{1} – r_{2})^{2}}\); [As PT = WX]

Note: This formula remains true even when the circles touch or intersect each other.

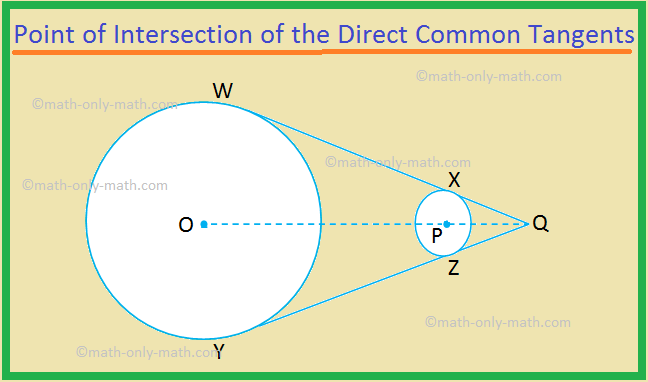
III. The point of intersection of the direct common tangents and the centres of the circles are collinear.

Given: Two circles with centres O and P, and there direct common tangents WX and YZ, which intersect at Q.

To prove: Q, P and O lie on the same straight line.

Proof:

10th Grade Math

From Important Properties of Direct Common Tangents to HOME PAGE