Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Highest Common Factor (HCF)
Highest common factor (H.C.F) of two or more numbers is the greatest number which divides each of them exactly.
Highest Common Factor (HCF) is also called Greatest Common Divisor (GCD) or Greatest Common Factor (GCF).
A number is said to be a common factor of two or more numbers, if it is a factor of each of them.
For example:
The factors of 6 are 1, 2, 3 and 6.
The factors of 12 are 1, 2, 3, 4, 6 and 12.
The numbers 1, 2, 3 and 6 are the factors of both 6 and 12.
Therefore 1, 2, 3 and 6 are the common factors of 6 and 12.
The highest common factor (HCF) of two or more given numbers is the highest, i.e., greatest of their common factors.
It is also known as the Greatest Common Divisor (GCD).
Let us consider the numbers 21 and 42.
All the factors of 21 are 1, 3, 7 and 21.
All the factors of 42 are 1, 2, 3, 6, 7, 21 and 42.
The Common factors of 21 and 42 are 1, 3, 7 and 21.
21 is the greatest common factor of 21 and 42.
Hence, HCF of 21 and 42 is 21.
✍️ Now we will learn about the method of finding highest common factor (H.C.F).
Steps 1:
Find all the factors of each given number.
Step 2:
Find common factors of the given number.
Step 3:
The greatest of all the factors obtained in Step 2, is the required highest common factor (H.C.F).
For Example:
1. Find the highest common factor (H.C.F) of 6 and 9.
Factors of 6 = 1, 2, 3 and 6.
Factors of 9 = 1, 3 and 9.
Therefore, common factor of 6 and 9 = 1 and 3.
Highest common factor (H.C.F) of 6 and 9 = 3.
Therefore, 3 is H.C.F. or G.C.D. greatest common divisor of 6 and 9.
H.C.F. or G.C.D. of given numbers is the greatest number which divides all the numbers without leaving a remainder.
2. Find the highest common factor (H.C.F) of 6 and 8.
Factors of 6 = 1, 2, 3 and 6.
Factors of 8 = 1, 2, 4 and 8.
Therefore, common factor of 6 and 8 = 1 and 2.
Highest common factor (H.C.F) of 6 and 8 = 2.
Therefore, 2 is H.C.F. or G.C.D. greatest common divisor of 6 and 8.
3. Find the highest common factor (H.C.F) of 14 and 18.
Factors of 14 = 1, 2, 7 and 14.
Factors of 18 = 1, 2, 3, 6, 9 and 18.
Therefore, common factor of 14 and 18 = 1 and 2.
Highest common factor (H.C.F) of 14 and 18 = 2.
Note: The highest common factor or HCF of two or more numbers is the greatest number that divides exactly the given numbers.
4. Find the highest common factor (H.C.F) of 15 and 10.
Factors of 15 = 1, 3, 5 and 15.
Factors of 10 = 1, 2, 5 and 10.
Therefore, common factor of 15 and 10 = 1 and 5.
Highest common factor (H.C.F) of 15 and 10 = 5.
5. Find the highest common factor (H.C.F) of 12 and 18.
Factors of 12 = 1, 2, 3, 4, 6 and 12.
Factors of 18 = 1, 2, 3, 6, 9 and 18.
Therefore, common factor of 12 and 18 = 1, 2, 3 and 6.
Highest common factor (H.C.F) of 12 and 18 = 6 [since 6 is the highest common factor].
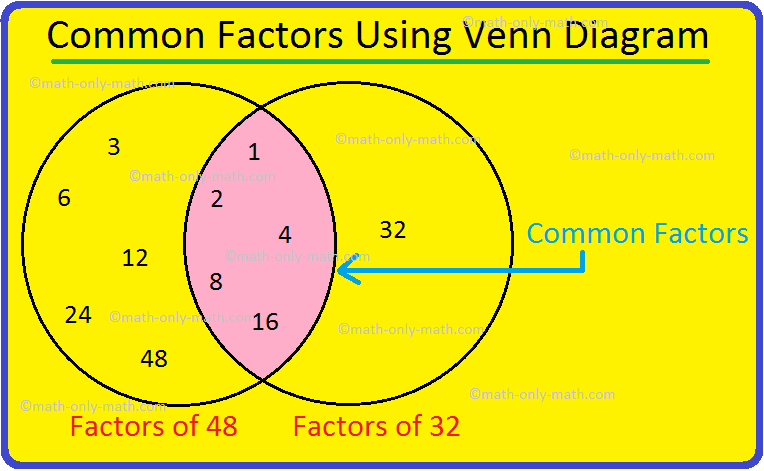
6. Find the highest common factor (H.C.F) of 48 and 32.
Solution:
Factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24 and 48
Factors of 32 = 1, 2, 4, 8, 16 and 32
Therefore, the common factors are 1, 2, 4, 8 and 16.
The highest common factor is 16.
Thus, highest common factor (HCF) of 48 and 32 is 16.
The common factors can be represented using venn diagram as given below.
7. Find the highest common factor (H.C.F) of 24 and 36.
Factors of 24 = 1, 2, 3, 4, 6, 8, 12 and 24.
Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18 and 36.
Therefore, common factor of 24 and 36 = 1, 2, 3, 4, 6 and 12.
Highest common factor (H.C.F) of 24 and 36 = 12.
8. Let us find the HCF of two numbers 15 and 18.
The factors of 15 are 1, 3, 5, 15
The factors of 18 are 1, 2, 3, 6 ,9, 18
The common factors of 15 and 18 are 1, 3.
Clearly, the highest of these common factors is 3.
Therefore, 3 is the HCF of 15 and 18.
We can find the Highest Common Factor (HCF) by the following two methods:
I: Prime Factorization Method
II: Division Method
I: Prime Factorization Method:
Working Rules to find the HCF by Prime Factorization Method:
Step I: Find the prime factors of each of the given number by the prime factorization method.
Step II: Multiply all the 'common' prime factors to get the HCF of the given numbers.
For Example:
1. Find the HCF of 72 and 48.
Solution:
Find the prime factor of both the numbers
Prime factors of
72 = 2 × 2 × 2 × 3 × 3
48 = 2 × 2 × 2 × 2 × 3
Hence, the common factors are 2, 2, 2 and 3.
The required HCF = 2 × 2 × 2 × 3 = 24
Note: If one out of the two given numbers is a factor of the other, then the smaller number is the required HCF of the given numbers.
For Example:
HCF of 6 and 36 is 6.
Since 6 is the factor of 36.
2. Find the HCF of 24 and 36 using prime factorisation method.
Solution:
Let us Find the prime factor of both the numbers 24 and 36.
All possible factors of 24 = 2 × 2 × 2 × 3
All possible factors of 36 = 2 × 2 × 3 × 3
Hence, the common factors are 2, 2 and 3.
The product of common factors of 24 and 36 are 2 × 2 × 3
Thus (Highest Common Factor) HCF of 24 and 36 is 2 × 2 × 3 = 12.
Note: Always take the prime numbers from the lowest, i.e., 2, 3, 5, 7, 11, 13, 17, ... and divide as often as possible by any one before going to the next.
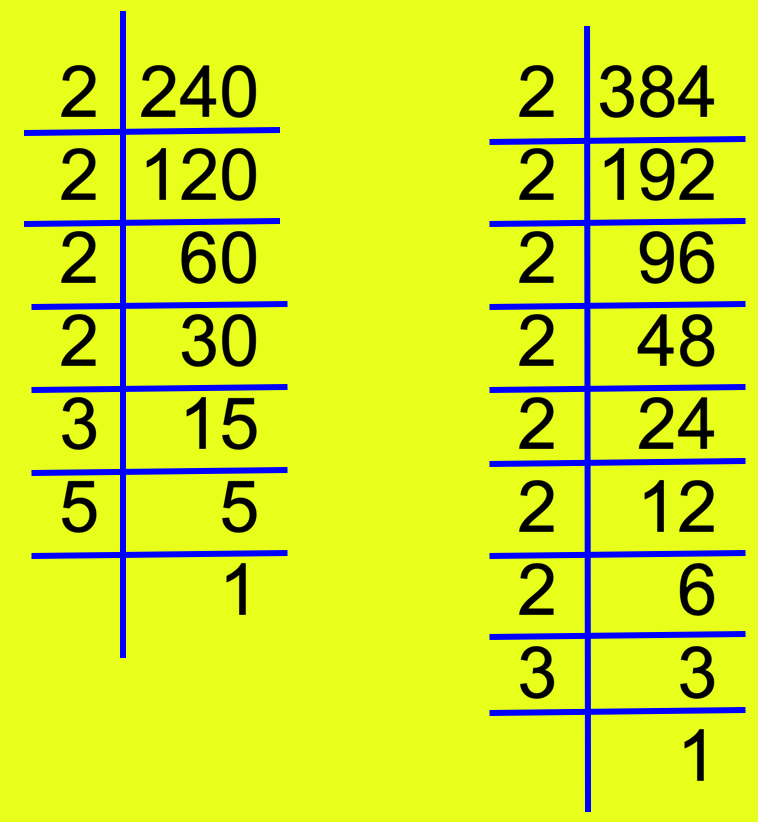
3. Find the HCF (Highest Common Factor) of 240 and 384 using prime factorisation method.
Solution:
First, we find the prime factorisation of the given numbers.
The prime factorisation of:
240 = 2 × 2 × 2 × 2 × 3 × 5.
384 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3.
The common factors are 2, 2 , 2 , 2 and 3.
Therefore, HCF = 2 × 2 × 2 × 2 × 3 = 48.
Hence, the HCF of 240 and 384 is 48.
4. Find the HCF (Highest Common Factor) of 21 and 85 using prime factorisation method.
Solution:
First, we find the prime factorization of the given numbers.
The prime factorisation of 21 is 3 × 7.
The prime factorisation of 85 is 5 × 17.
As there is no common factor, so their HCF is 1.
Note: When two numbers have their HCF 1, they are said to be co-prime.
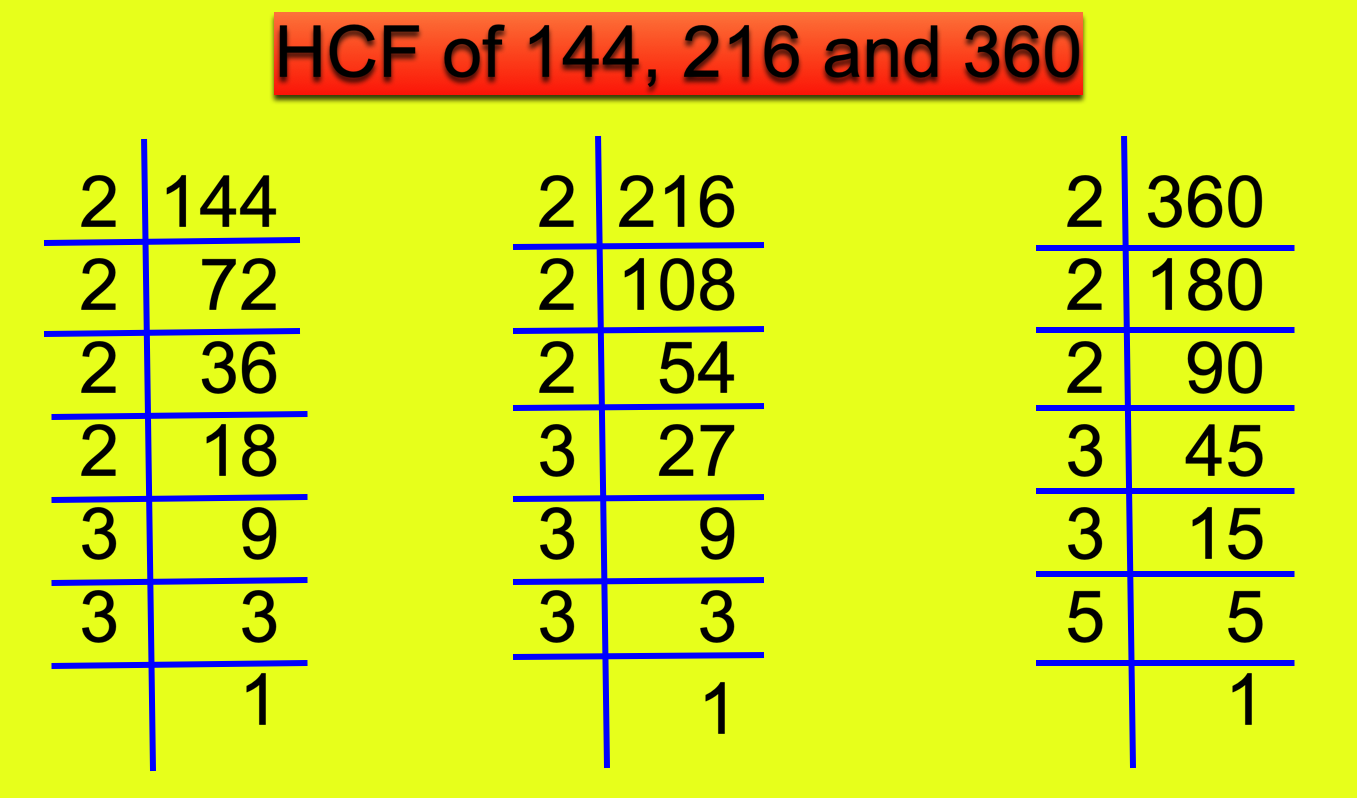
5. Find the HCF (Highest Common Factor) of three numbers 144, 216 and 360 by prime factorisation method.
Solution:
First, we find the prime factorisation of the given numbers.
Here, 144 = 2 × 2 × 2 × 2 × 3 × 3
216 = 2 × 2 × 2 × 3 × 3 × 3
360 = 2 × 2 × 2 × 3 × 3 × 5
Common factors are 2, 2, 2, 3 and 3.
Therefore, HCF = 2 × 2 × 2 × 3 × 3 = 72.
Hence, the required HCF is 72.
II: Division Method:
Working Rules to find the HCF of Two Numbers by Division Method:
Step I: Divide the greater number by the smaller one.
Step II: Divide the divisor by the remainder.
Step III: Continue the steps I to II till the remainder becomes zero.
For Example:
1. Find the HCF of 14 and 49 using the division method.
Solution:
Here, the last divisor is 7.
Therefore, the highest common factor (HCF) of 14 and 49 is 7.
2. Find the HCF of 198 and 360 using the long division method.
Solution:
Here, the last divisor is 18.
So, the HCF of 198 and 360 = 18.
3. Find the HCF of 144 and 180 by using the long division method.
Hence, the HCF of 144 and 180 is 36.
HCF of Three or More Numbers Using Division Method:
Working Rules to find the HCF of Three or More Numbers by Division Method:
Step I: : Find the HCF of any two numbers.
Step II: Find the HCF of third number and the HCF obtained in step I.
For Example:
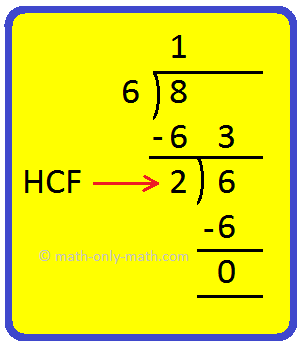
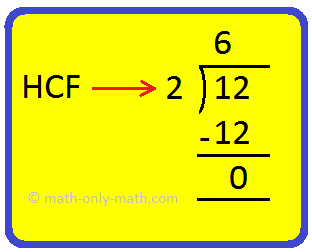
1. Find the HCF of 6, 8 and 12.
Solution:
Step I: Finding the HCF of 6 and 8
Step II: Finding the HCF of 2 and 12
Hence, the HCF of 6, 8 and 12 is 2.
Note: We can verify the result by the factorisation method also.
2. Find the HCF (Highest Common Factor) of 875 and 1225 by long division method.
Solution:
Remainder is zero.
The last divisor is 175.
Hence, the HCF of 875 and 1225 is the last divisor, i.e., 175.
1. What are the methods of prime factorisation?
1. What are the methods of prime factorisation?
Answer:
There are two methods to find the HCF of two or more numbers:
I. Prime factorisation method
II. Division method
2. How to find the HCF by prime factorization method?
2. How to find the HCF by prime factorization method?
Answer:
Finding the HCF by the Prime Factorisation Method
The HCF of two or more numbers can be determined by resolving each nun factors and multiplying the common prime factors of the numbers.
To find HCF, follow these steps:
Step I: Break up each number into its prime factors.
Step II: Take out the common prime factors which are found in the numbers and omit others.
Step III: Multiply the common factors together. The product, thus, obtained is the HCF of given numbers. When there is no common factor in the given numbers, common factor is 1. So, the HCF will be 1.
3. How to find the HCF by division method?
3. How to find the HCF by division method?
Answer:
Finding the HCF by the Division Method
This method is usually used for large numbers.
Step I: Divide the greater number by the smaller number.
Step II: Divide the first divisor by the remainder.
Step III: Go on dividing the divisors by the remainders till the remainder is zero.
Step IV: The last divisor will be the HCF of the given numbers.
● Factors.
● Highest Common Factor (H.C.F).
● Examples on Highest Common Factor (H.C.F).
● Greatest Common Factor (G.C.F).
● Examples of Greatest Common Factor (G.C.F).
● To find Highest Common Factor by using Prime Factorization Method.
● Examples to find Highest Common Factor by using Prime Factorization Method.
● To find Highest Common Factor by using Division Method.
● Examples to find Highest Common Factor of two numbers by using Division Method.
● To find the Highest Common Factor of three numbers by using Division Method.
From Highest Common Factor to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.

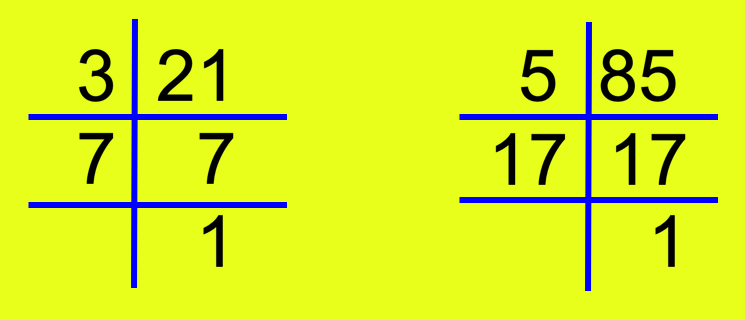
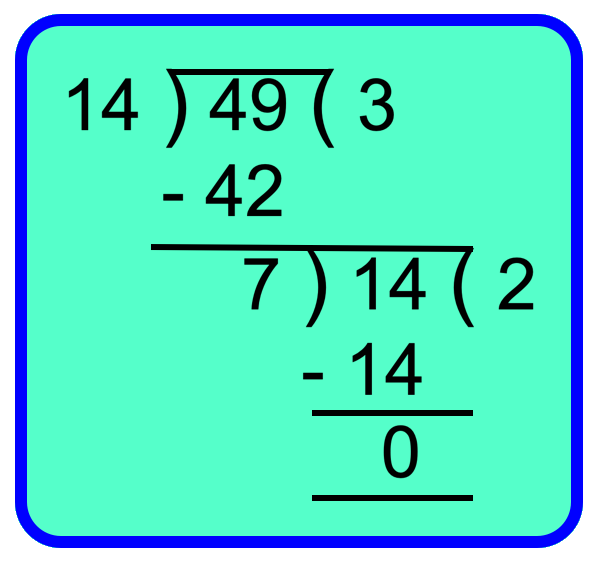





New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.