Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Word problems on H.C.F. and L.C.M.
Here we will get the idea how to solve the word problems on H.C.F and L.C.M.
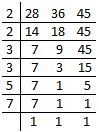
1. Find the smallest number which on adding 19 to it is exactly divisible by 28, 36 and 45.
First we find the least common multiple (L.C.M.) of 28, 36 and 45.
Therefore, least common multiple (L.C.M.) of 28, 36 and 45 = 2 × 2 × 3 × 3 × 5 × 7 = 1260
Therefore, the required number = 1260 - 19 = 1241
2. Find the number which divides 167 and 95 leaving 5 as remainder.
The number divides 167 and leaves 5 as remainder
Therefore, the number divides 167 - 5 = 162 exactly
The number also divides 95 leaving 5 as remainder
Therefore, the number divides 95 - 5 = 90 exactly
Now we have to find highest common factor (H.C.F.) of 162 and 90
Highest common factor (H.C.F.) of 90 and 162 = 18
Therefore, 18 is the required number.
3. Find the largest number that divides 92 and 74 leaving 2 as remainder.
The number divides 92 and leaves 2 as remainder
Therefore, the number divides 92 - 2 = 90 exactly
The number also divides 74 leaving 2 as remainder
Therefore, the number divides 74 - 2 = 72 exactly
Now we have to find highest common factor (H.C.F.) of 90 and 72
Highest common factor (H.C.F.) of 90 and 72 = 18
Therefore, 18 is the required number.
4. Nairitee saves $8.85 daily. Find the least number of days in which she will be able to save an exact number of dollars.
Solution:
The number of dollars will always be a multiple of 100 cents, like:
2 = 2 × 100 cents = 200 cents
5 = 5 × 100 cents = 500 cents
We know that $8.85 = 885 cents.
Hence, saved money will be a multiple of 885 cents.
Now, the LCM of 100 and 885 is as follows:
5 | 100, 885
20, 177
LCM of 100 and 885 = 17700
So, Nairitee saves 17700 cents.
Therefore, the required number of days = 17700/885 = 20 days.
5. Find the least number which, when divided by 12, 22 and 26, leaves a remainder of 7 in each case.
Solution:
The least number which is exactly divisible by 12, 22 and 26 is the LCM of these numbers.
Let us find the LCM of 12, 22 and 26.
Prime factorization of the numbers 12, 22 and 26.
12 = 2 × 2 × 3
22 = 2 × 11
26 = 2 × 13
Therefore, the LCM of (12, 22, 26) = 2 × 2 × 3 × 11 × 13 = 1716
But, the required number is a number that leaves a remainder of 7 in each case.
That means the required number is 7 more than the LCM.
Required number 1716 + 7 = 1723.
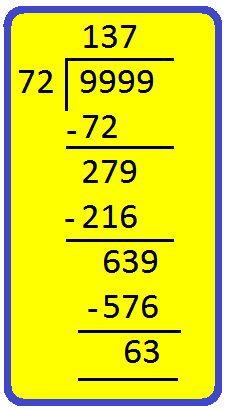
6. Find the greatest 4-digit number which when divided by 12, 18 and 24 leaves a remainder of 5 in each case.
Solution:
First, we find the LCM of 12, 18 and 24 as shown below.
Prime factorization of the numbers 12, 18 and 24
12 = 2 × 2 × 3
18 = 2 × 3 × 3
24 = 2 × 2 × 2 × 3
Therefore, LCM of 12, 18 and 24 = 2 × 2 × 2 × 3 × 3 = 72
Hence, 72 is the least number divisible by 12, 18 and 24.
Now, the greatest 4-digit number is 9999.
So, we have to find the greatest multiple of 72 which is just less than 9999.
To find the number, we have to divide 9999 by 72.
Now, 9999 - 63= 9936, which is exactly divisible by 72 (i.e., divisible by 12, 18 and 24 also).
But, the required number leaves a remainder 5 in each case.
Hence, the required number = 9936 + 5 = 9941.
7. Find the largest number that will divide 251, 361 and 487 leaving remainders 3, 5 and 7 respectively.
Solution:
We find that
251 - 3 = 248
361 - 5 = 356
487 - 7 = 480
Now, the numbers exactly divisible are 248, 356 and 480.
Let us first find the HCF of 248 and 356 as shown below.
Thus, the HCF of 248 and 356 = 4.
Now, we find the HCF of 4 and 480.
The HCF of 4 and 480 = 4
Thus, the HCF of 248, 356 and 480 = 4.
Hence, the required largest number = 4.
8. Find the number nearest to hundred thousand (one-lakh) but must greater than hundred thousand (one-lakh) which is exactly divisible by 4, 12 and 18.
Solution:
First, we find the LCM of 4, 12 and 18.
Prime factorization of the numbers 4, 12 and 18.
4 = 2 × 2
12 = 2 × 2 × 3
18 = 2 × 3 × 3
Therefore, the LCM of 4, 12 and 18 = 2 × 2 × 3 × 3 = 36
Now, we divide 100000 by 36 as shown below.
Therefore, the number nearest to 100000 and divisible by 36 (i.e. divisible by 4, 12, and 18), is equal to (100000 - 28) = 99972.
But, since 99972 is less than 100000, the next number which would be divisible by 36 (i.e. divisible by 4, 12, and 18), will be 99972 + 36 = 100008 which is greater than 100000.
Therefore the the required number = 100800.
Least Common Multiple (L.C.M).
To find Least Common Multiple by using Prime Factorization Method.
Examples to find Least Common Multiple by using Prime Factorization Method.
To Find Lowest Common Multiple by using Division Method
Examples to find Least Common Multiple of two numbers by using Division Method
Examples to find Least Common Multiple of three numbers by using Division Method
Relationship between H.C.F. and L.C.M.
Worksheet on H.C.F. and L.C.M.
Word problems on H.C.F. and L.C.M.
Worksheet on word problems on H.C.F. and L.C.M.
From Word problems on H.C.F. and L.C.M. to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.

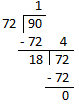




New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.