Worksheet on Methods of Prime Factorization
Practice the questions given in the worksheet on methods of prime factorization.
1. Each of the following is the prime factorization of a certain number. Find the number.
(i) 2 × 5 × 7
(ii) 3 × 7 × 7
(iii) 2 × 7 × 13
(iv) 2 × 2 × 3 × 5
(v) 7 × 11 × 11
(vi) 5 × 5 × 7
(vii) 3 × 3 × 7
(viii) 2 × 3 × 3 × 7
(ix) 3 × 5 × 5 × 7
2. Find the prime factors by division method.
(i) 42
(ii) 95
(iii) 4
(iv) 94
(v) 28
(vi) 52
(vii) 40
(viii) 84
3. Find the prime factors by factor method.
(i) 30
(ii) 36
(iii) 5
(iv) 27
(v) 72
(vi) 56
(vii) 80
(viii) 96
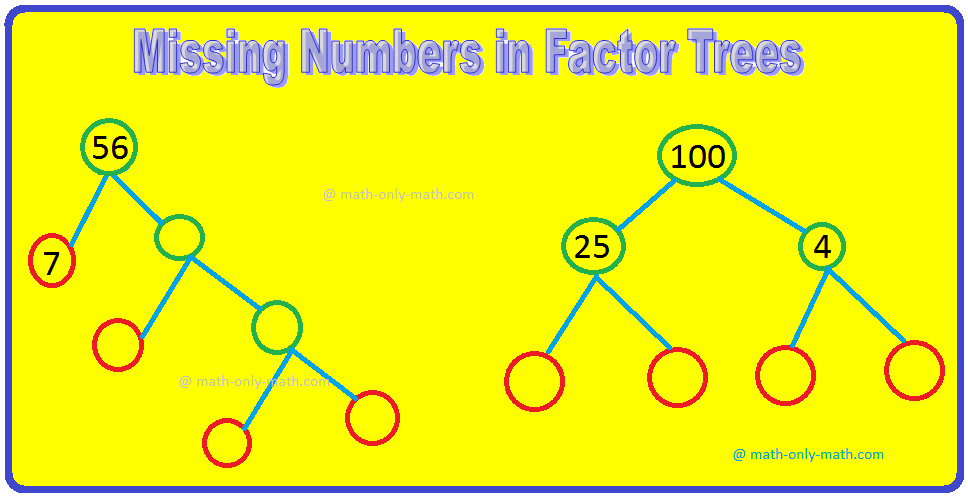
4. Write the missing numbers in the factor trees.
5. Determine the prime factorization by any method you like.
(i) 2
(ii) 86
(iii) 50
(iv) 68
(v) 74
(vi) 90
(vii) 88
(viii) 48
(ix) 81
(x) 42
(xi) 66
(xii) 45
6. Multiple Choice Questions (MCQ) on Prime Factorization:
Tick (✔) the correct option.
(i) Prime factorisation of 54 is:
(a) 2 × 27
(b) 2 × 3 × 9
(c) 54 × 1
(d) 2 × 3 × 3 × 3
(ii) 2 × 3 × 7 is the prime factorisation of
(a) 21
(b) 1237
(c) 237
(d) 42
7. Find the prime factorisation of the following numbers:
(i) 18
(ii) 34
(iii) 385
(iv) 45
(v) 52
(vi) 64
(vii) 390
(viii) 2520
(ix) 1210
(x) 1260
(xi) 1024
(xii) 2520
Answers for the worksheet on methods of prime factorization are given below.
Answers:
1. (i) 10
(ii) 147
(iii) 182
(iv) 60
(v) 847
(vi) 175
(vii) 63
(viii) 126
(ix) 525
2. (i) 2 × 3 × 7
(ii) 5 × 19
(iii) 2 × 2
(iv) 2× 47
(v) 2 × 2 × 7
(vi) 2 × 2 × 13
(vii) 2 × 2 × 2 × 5
(viii) 2 × 2 × 3 × 7
3. (i) 2 × 3 × 5
(ii) 2 × 2 × 3 × 3
(iii) 1 × 5
(iv) 3 × 3 × 3
(v) 2 × 2 × 2 × 3 × 3
(vi) 2 × 2 × 2 × 7
(vii) 2 × 2 × 2 × 2 × 5
(viii) 2 × 2 × 2 × 2 × 2 × 3
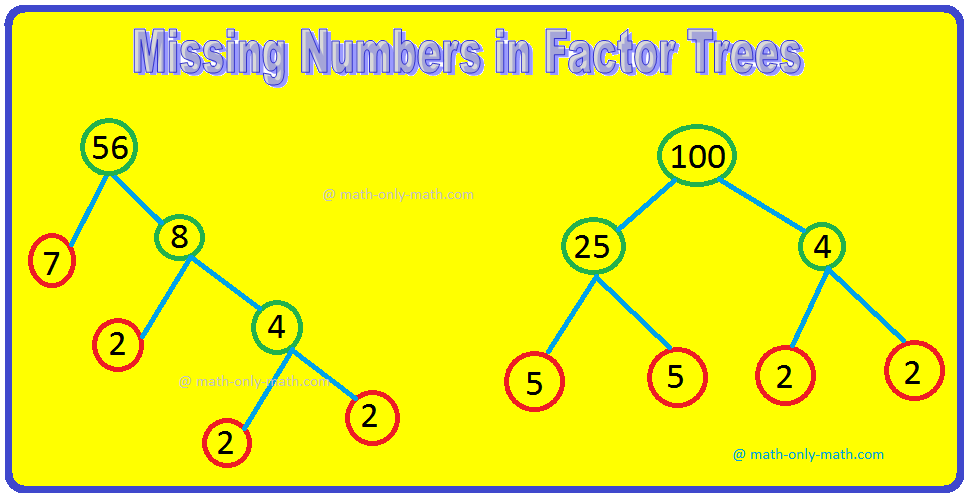
4.
5. (i) 1 × 2
(ii) 2 × 43
(iii) 2 × 5 × 5
(iv) 2 × 2 × 17
(v) 2 × 37
(vi) 2 × 5 × 9
(vii) 2 × 2 × 2 × 11
(viii) 2 × 2 × 2 × 2 × 3
(ix) 3 × 3 × 3 × 3
(x) 2 × 3 × 7
(xi) 2 × 3 × 11
(xii) 3 × 3 × 5
6. (d) 2 × 3 × 3 × 3
(ii) (d) 42
7. (i) 18 = 1 × 2 × 3 × 3
(ii) 34 = 1 × 3 × 13
(iii) 385 = 1 × 5 × 7 × 11
(iv) 45 = 1 × 3 × 3 × 5
(v) 52 = 1 × 2 × 2 × 13
(vi) 64 = 1 × 2 × 2 × 2 × 2 × 2 × 2 × 2
(vii) 390 = 2 × 3 × 5 × 13
(viii) 2520 = 1 × 2 × 2 × 2 × 3 × 3 × 5 × 7
(ix) 1210 = 2 × 5 × 11 × 11
(x) 1260 = 1 × 2 × 2 × 3 × 3 × 5 × 7
(xi) 1024 = 1 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
(xii) 2520 = 1 × 2 × 2 × 2 × 3 × 3 × 5 × 7
You might like these
Highest Common Factor |Find the Highest Common Factor (H.C.F)|Examples
Highest common factor (H.C.F) of two or more numbers is the greatest number which divides each of them exactly. Now we will learn about the method of finding highest common factor (H.C.F). Steps 1: Find all the factors of each given number. Step 2: Find common factors of the
Prime Factorisation |Complete Factorisation |Tree Factorisation Method
Prime factorisation or complete factorisation of the given number is to express a given number as a product of prime factor. When a number is expressed as the product of its prime factors, it is called prime factorization. For example, 6 = 2 × 3. So 2 and 3 are prime factors
Multiples and Factors | Infinite Factors | Multiply Counting Numbers
We will discuss here about multiples and factors and how they are related to each other. Factors of a number are those numbers which can divide the number exactly. For example, 1, 2, 3 and 6 are
Divisible by 3 | Test of Divisibility by 3 |Rules of Divisibility by 3
A number is divisible by 3, if the sum of its all digits is a multiple of 3 or divisibility by 3. Consider the following numbers to find whether the numbers are divisible or not divisible by 3: (i) 54 Sum of all the digits of 54 = 5 + 4 = 9, which is divisible by 3.
Divisible by 4 | Test of Divisibility by 4 |Rules of Divisibility by 4
A number is divisible by 4 if the number is formed by its digits in ten’s place and unit’s place (i.e. the last two digits on its extreme right side) is divisible by 4. Consider the following numbers which are divisible by 4 or which are divisible by 4, using the test of
Divisible by 5 | Test of divisibility by 5| Rules of Divisibility by 5
Divisible by 5 is discussed below: A number is divisible by 5 if its units place is 0 or 5. Consider the following numbers which are divisible by 5, using the test of divisibility by
Divisible by 6 | Test of Divisibility by 6| Rules of Divisibility by 6
Divisible by 6 is discussed below: A number is divisible by 6 if it is divisible by 2 and 3 both. Consider the following numbers which are divisible by 6, using the test of divisibility by 6: 42
Divisible by 8 | Test of Divisibility by 8 |Rules of Divisibility by 8
Divisible by 8 is discussed below: A number is divisible by 8 if the numbers formed by the last three digits is divisible by 8. Consider the following numbers which are divisible by 8
Divisible by 7 | Test of Divisibility by 7 |Rules of Divisibility by 7
Divisible by 7 is discussed below: We need to double the last digit of the number and then subtract it from the remaining number. If the result is divisible by 7, then the original number will also be
Divisible by 9 | Test of Divisibility by 9 |Rules of Divisibility by 9
A number is divisible by 9, if the sum is a multiple of 9 or if the sum of its digits is divisible by 9. Consider the following numbers which are divisible by 9, using the test of divisibility by 9:
Divisible by 10|Test of Divisibility by 10|Rules of Divisibility by 10
Divisible by 10 is discussed below. A number is divisible by 10 if it has zero (0) in its units place. Consider the following numbers which are divisible by 10, using the test of divisibility by 10:
Least Common Multiple |Lowest Common Multiple|Smallest Common Multiple
The least common multiple (L.C.M.) of two or more numbers is the smallest number which can be exactly divided by each of the given number. The lowest common multiple or LCM of two or more numbers is the smallest of all common multiples.
Multiples | Multiples of a Number |Common Multiple|First Ten Multiples
What are multiples? ‘The product obtained on multiplying two or more whole numbers is called a multiple of that number or the numbers being multiplied.’ We know that when two numbers are multiplied the result is called the product or the multiple of given numbers.
Even and Odd Numbers Between 1 and 100 | Even and Odd Numbers|Examples
All the even and odd numbers between 1 and 100 are discussed here. What are the even numbers from 1 to 100? The even numbers from 1 to 100 are:
Prime and Composite Numbers | Prime Numbers | Composite Numbers
What are the prime and composite numbers? Prime numbers are those numbers which have only two factors 1 and the number itself. Composite numbers are those numbers which have more than two factors.
From Worksheet on Methods of Prime Factorization to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Adding 1-Digit Number | Understand the Concept one Digit Number
Sep 17, 24 02:25 AM
Understand the concept of adding 1-digit number with the help of objects as well as numbers. -
Counting Before, After and Between Numbers up to 10 | Number Counting
Sep 17, 24 01:47 AM
Counting before, after and between numbers up to 10 improves the child’s counting skills. -
Worksheet on Three-digit Numbers | Write the Missing Numbers | Pattern
Sep 17, 24 12:10 AM
Practice the questions given in worksheet on three-digit numbers. The questions are based on writing the missing number in the correct order, patterns, 3-digit number in words, number names in figures… -
Arranging Numbers | Ascending Order | Descending Order |Compare Digits
Sep 16, 24 11:24 PM
We know, while arranging numbers from the smallest number to the largest number, then the numbers are arranged in ascending order. Vice-versa while arranging numbers from the largest number to the sma… -
Worksheet on Tens and Ones | Math Place Value |Tens and Ones Questions
Sep 16, 24 02:40 PM
In math place value the worksheet on tens and ones questions are given below so that students can do enough practice which will help the kids to learn further numbers.
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.