Finding the Median of Grouped Data
To find the median of arrayed (grouped) data we need to follow the following steps:
Step I: Arrange the grouped data in ascending or descending order, and form a frequency table.
Step II: Prepare a cumulative-frequency table of the data.
Step III: Select the cumulative frequency that is just greater than N2, where N is the total number of observations (variates). Then find the median as follows.
The variate whose cumulative frequency is the selected cumulative frequency, is the median of the data.
If N2 is equal to the cumulative frequency of a variate then
median = mean of this variate and the variate just greater than it.
Solved Examples on Find the Median of Grouped Data /Arrayed Data:
1. Find the median of the following distribution.
Variate
2
5
6
8
10
Number of Students
3
2
5
4
2
Solution:
Here, the frequency distribution is given.
The cumulative-frequency table of the distribution is
|
Variates 2 5 6 8 10 |
Frequency 3 2 5 4 2 N = 16 |
Cumulative Frequency 3 5 10 14 16 |
Here, N2 = 162 = 8.
The cumulative frequency just greater than 8 is 10.
The variate whose cumulative frequency is 10 is 6.
Therefore, the median = 6.
2. Find the median of the arrayed data given below.
10, 11, 11, 12, 12, 12, 13, 14, 14, 15, 15, 15, 15, 16, 16, 17, 18, 19, 19, 20.
Solution:
Putting the data in a frequency table, we have the cumulative frequencies as below.
Here, the total frequency N = 20.
So, N2 = 202 = 10.
The cumulative frequency just greater than 10 is 13 and the corresponding variates is 15. So, the median = 15.
From Finding the Median of Grouped Data to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
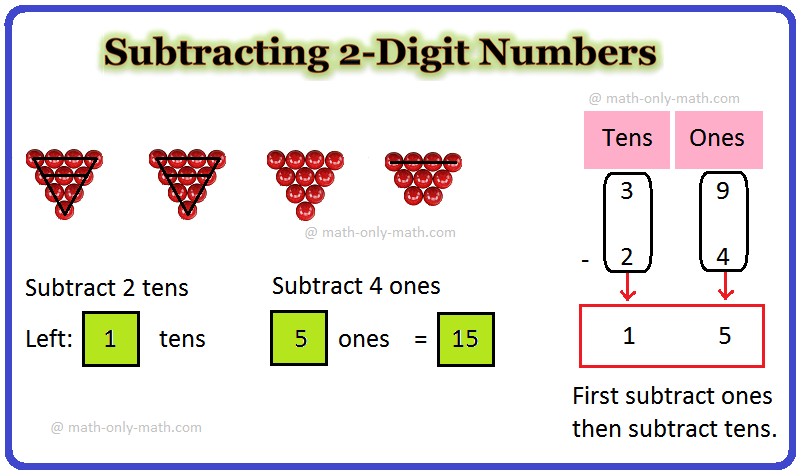
Subtracting 2-Digit Numbers Video | How to Subtract Two Digit Numbers?
Apr 01, 25 02:15 AM
In subtracting 2-digit numbers we will subtract or minus a two-digit number from another two-digit number. To find the difference between the two numbers we need to ‘ones from ones’ and ‘tens from -
PEMDAS Rule | Steps to Simplify the Order of Operation | Simple Rules
Apr 01, 25 02:10 AM
Easy and simple way to remember PEMDAS rule!! P → Parentheses first E → Exponent (Powers, Square Roots, Cube Roots, etc.) MD → Multiplication and Division (start from left to right) AS → -
Worksheet on Simplification | Simplify Expressions | BODMAS Questions
Apr 01, 25 01:59 AM
In worksheet on simplification, the questions are based in order to simplify expressions involving more than one bracket by using the steps of removal of brackets. This exercise sheet -
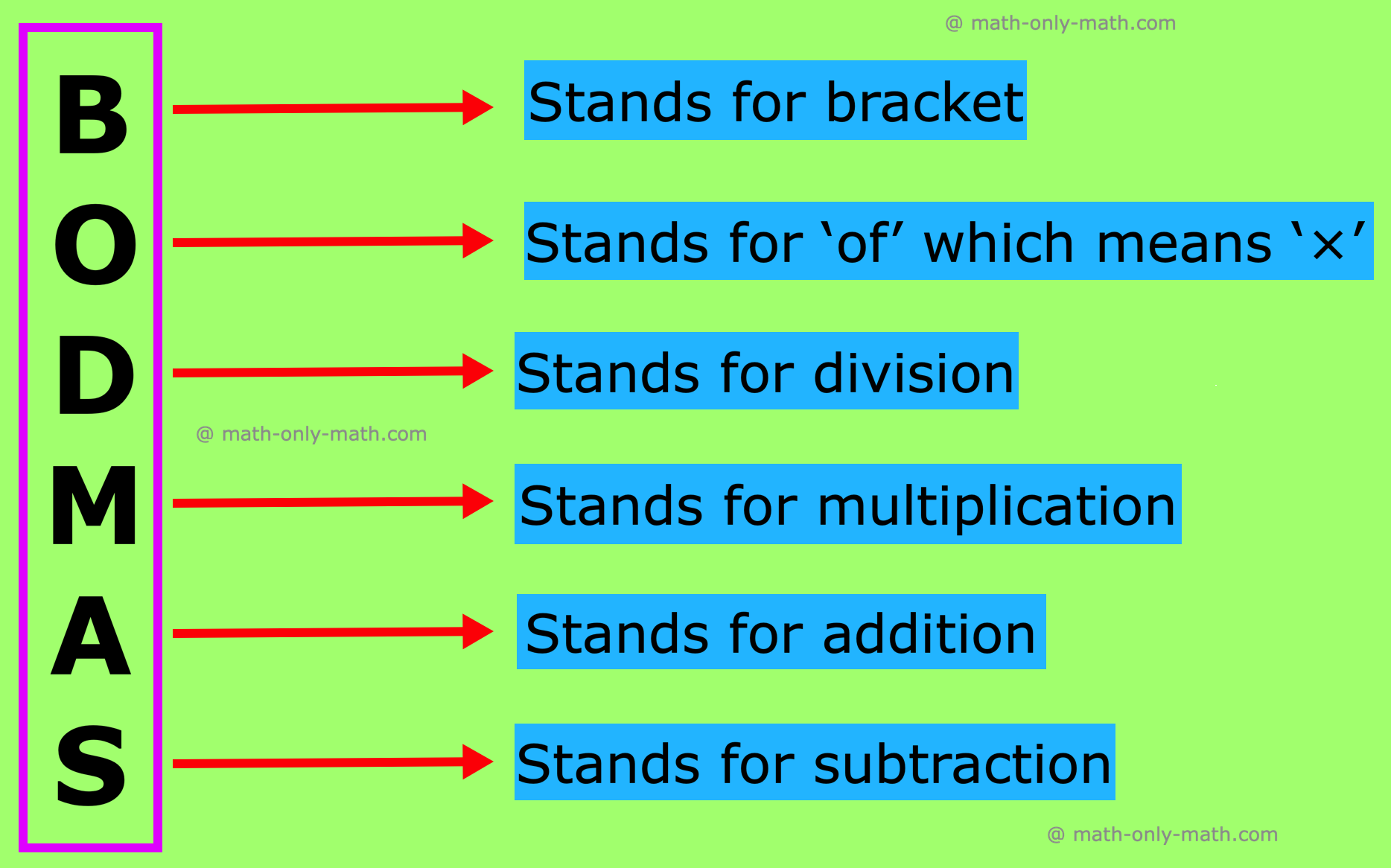
BODMAS Rule | Order of Operation | Definition, Examples, Problems
Mar 31, 25 11:35 PM
Easy and simple way to remember BODMAS rule!! B → Brackets first (parentheses) O → Of (orders i.e. Powers and Square Roots, Cube Roots, etc.) DM → Division and Multiplication -
Subtracting 1-Digit Number | Subtract Two One-Digit Number | Video
Mar 30, 25 10:16 AM
In subtracting 1-digit number we will subtract or minus one-digit number from one-digit number or one-digit number from 2-digit number and find the difference between them. We know that subtraction me…



New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.