Trigonometrical Ratios of (90° - θ)

What is the relation among all the trigonometrical ratios of (90° - θ)?

In trigonometrical ratios of angles (90° - θ) we will find the relation between all six trigonometrical ratios.

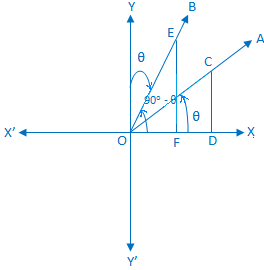
Let a rotating line OA rotates about O in the anti-clockwise direction, from initial position to ending position makes an angle ∠XOA = θ. Now a point C is taken on OA and draw CD perpendicular to OX or OX'.

Again another rotating line OB rotates about O in the anti-clockwise direction, from initial position to ending position (OX) makes an angle ∠XOY = 90°; this rotating line now rotates in the clockwise direction, starting from the position (OY) makes an angle ∠YOB = θ.

Now, we can observe that ∠XOB = 90° - θ.

Again a point E is taken on OB such that OC = OE and draw EF perpendicular to 

OX or OX'.

Since, ∠YOB = ∠XOA

Therefore, ∠OEF = ∠COD.

Now, from the right-angled ∆EOF and right-angled ∆COD we get, ∠OEF = ∠COD and OE = OC.

Hence, ∆EOF ≅ ∆COD (congruent).

Therefore, FE = OD, OF = DC and OE = OC.

According to the definition of trigonometric ratio we get,

sin (90° - θ) = \(\frac{FE}{OE}\)

sin (90° - θ) = \(\frac{OD}{OC}\), [FE = OD and OE = OC, since ∆EOF ≅ ∆COD]

sin (90° - θ) = cos θ

cos (90° - θ) = \(\frac{OF}{OE}\)

cos (90° - θ) = \(\frac{DC}{OC}\), [OF = DC and OE = OC, since ∆EOF ≅ ∆COD]

cos (90° - θ) = sin θ

tan (90° - θ) = \(\frac{FE}{OF}\)

tan (90° - θ) = \(\frac{OD}{DC}\), [FE = OD and OF = DC, since ∆EOF ≅ ∆COD]

tan (90° - θ) = cot θ

Similarly, csc (90° - θ) = \(\frac{1}{sin (90°  -  \Theta)}\) 

csc (90° - θ) = \(\frac{1}{cos \Theta}\)

csc (90° - θ) = sec θ

sec ( 90° - θ) = \(\frac{1}{cos (90°  -  \Theta)}\) 

sec (90° - θ) = \(\frac{1}{sin \Theta}\)

sec (90° - θ) = csc θ

and cot (90° - θ) = \(\frac{1}{tan (90°  -  \Theta)}\) 

cot (90° - θ) = \(\frac{1}{cot \Theta}\)

cot (90° - θ) = tan θ

Solved examples:

1. Find the value of cos 30°.

Solution:

cos 30° = sin (90 - 60)°

            = sin 60°; since we know, cos (90° - θ) = sin θ

              = \(\frac{√3}{2}\)

2. Find the value of csc 90°.

Solution:

csc 90° = csc (90 - 0)°

            = sec 0°; since we know, csc (90° - θ) = sec θ

              = 1

● Trigonometric Functions

• Basic Trigonometric Ratios and Their Names
• Restrictions of Trigonometrical Ratios
• Reciprocal Relations of Trigonometric Ratios
• Quotient Relations of Trigonometric Ratios
  
• Limit of Trigonometric Ratios
  
• Trigonometrical Identity
• Problems on Trigonometric Identities
• Elimination of Trigonometric Ratios
• Eliminate Theta between the equations
• Problems on Eliminate Theta
• Trig Ratio Problems
• Proving Trigonometric Ratios
• Trig Ratios Proving Problems
• Verify Trigonometric Identities
• Trigonometrical Ratios of 0°
• Trigonometrical Ratios of 30°
• Trigonometrical Ratios of 45°
• Trigonometrical Ratios of 60°
• Trigonometrical Ratios of 90°
• Trigonometrical Ratios Table
• Problems on Trigonometric Ratio of Standard Angle
  
• Trigonometrical Ratios of Complementary Angles
• Rules of Trigonometric Signs
• Signs of Trigonometrical Ratios
  
• All Sin Tan Cos Rule
• Trigonometrical Ratios of (- θ)
• Trigonometrical Ratios of (90° + θ)
• Trigonometrical Ratios of (90° - θ)
• Trigonometrical Ratios of (180° + θ)
• Trigonometrical Ratios of (180° - θ)
• Trigonometrical Ratios of (270° + θ)
• Trigonometrical Ratios of (270° - θ)
• Trigonometrical Ratios of (360° + θ)
• Trigonometrical Ratios of (360° - θ)
• Trigonometrical Ratios of any Angle
• Trigonometrical Ratios of some Particular Angles
• Trigonometric Ratios of an Angle
• Trigonometric Functions of any Angles
• Problems on Trigonometric Ratios of an Angle
• Problems on Signs of Trigonometrical Ratios

11 and 12 Grade Math

From Trigonometrical Ratios of (90° - θ) to HOME PAGE