Equations of the Bisectors of the Angles between Two Straight Lines

We will learn how to find the equations of the bisectors of the angles between two straight lines.

Prove that the equation of the bisectors of the angles between the lines a$_{1}$x + b$_{1}$y + c$_{1}$ = 0 and a$_{2}$x + b$_{2}$y + c$_{2}$ = 0 are given by $\frac{a_{1}x + b_{1}y + c_{1}}{\sqrt{a_{1}^{2} + b_{1}^{2}}}$ = ±$\frac{a_{2}x + b_{2}y + c_{2}}{\sqrt{a_{2}^{2} + b_{2}^{2}}}$.

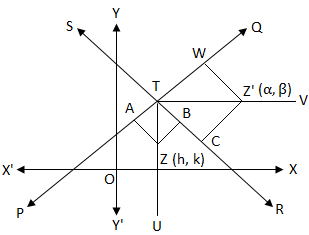
Let us assume the two given straight lines be PQ and RS whose equations are a$_{1}$x + b$_{1}$y + c$_{1}$ = 0 and a$_{2}$x + b$_{2}$y + c$_{2}$ = 0 respectively, where c$_{1}$ and c$_{2}$ are of the same symbols.

First we will find the equations of the bisectors of the angles between the lines a$_{1}$x + b$_{1}$y + c$_{1}$ = 0 and a$_{2}$x + b$_{2}$y + c$_{2}$ = 0.

Now, let us assume that the two straight lines PQ and RS intersect at T and ∠PTR contains origin O.

Equations of the Bisectors of the Angles between Two Straight Lines

Again, let us assume that TU is the bisector of ∠PTR and Z(h, k) is any point on TU. Then the origin O and the point Z are on the same side of both the lines PQ and RS.

Therefore, c$_{1}$, and (a$_{1}$h + b$_{1}$k + c$_{1}$) are of the same symbols and c$_{2}$ and (a$_{2}$h + b$_{2}$k + c$_{2}$) are also of the same symbols.

Since, we already assumed that c$_{1}$, and c$_{2}$, are of the same symbols, thus, (a$_{1}$h + b$_{1}$k + c$_{1}$) and (a$_{2}$h + b$_{2}$k + c$_{2}$) shall be of the same symbols.

Therefore, the lengths of the perpendiculars from Z upon PQ and RS are of the same symbols. Now, if ZA ⊥ PQ and ZB ⊥ RS then it implies that ZA = ZB.

⇒ $\frac{a_{1}h + b_{1}k + c_{1}}{\sqrt{a_{1}^{2} + b_{1}^{2}}}$ = $\frac{a_{2}h + b_{2}k + c_{2}}{\sqrt{a_{2}^{2} + b_{2}^{2}}}$

Therefore, the equation to the locus of Z (h, k) is,

$\frac{a_{1}x + b_{1}y + c_{1}}{\sqrt{a_{1}^{2} + b_{1}^{2}}}$ = $\frac{a_{2}x + b_{2}y + c_{2}}{\sqrt{a_{2}^{2} + b_{2}^{2}}}$………… (i), which is the equation of the bisector of the angle containing the origin.

Algorithm to find the bisector of the angle containing the origin:

Let the equations of the two lines be a$_{1}$x + b$_{1}$y + c$_{1}$ = 0 and a$_{2}$x + b$_{2}$y + c$_{2}$ = 0.

To find the bisector of the angle containing the origin, we proceed as follows:

Step I: First check whether the constant terms c$_{1}$ and c$_{2}$ in the given equations of two straight lines are positive or not. Suppose not, then multiply both the sides of the equations by -1 to make the constant term positive.

Step II: Now obtain the bisector corresponding to the positive symbol i.e. 

$\frac{a_{1}x + b_{1}y + c_{1}}{\sqrt{a_{1}^{2} + b_{1}^{2}}}$ = + $\frac{a_{2}x + b_{2}y + c_{2}}{\sqrt{a_{2}^{2} + b_{2}^{2}}}$, which is the required bisector of the angle containing the origin.

Note:

The bisector of the angle containing the origin means the bisector of that angle between the two straight lines which contains the origin within it.

Again, ∠QTR does not contain the origin. Suppose, TV be the bisector of ∠QTR and Z'(α, β) be any point on TV then the origin O and Z' are on the same side of the straight line (PQ) but they are on opposite sides of the straight line RS.

Therefore, c$_{1}$ and (a$_{1}$α + b$_{1}$β + c$_{1}$) are of the same symbols but c$_{2}$ and (a$_{2}$α + b$_{2}$β + c$_{2}$), are of opposite symbols.

Since, we already assumed that, c$_{1}$, and c$_{2}$, are of the same symbols, thus, (a$_{1}$α + b$_{1}$β + c$_{1}$) and (a$_{2}$α + b$_{2}$β + c$_{2}$) shall be of opposite symbols.

Therefore, the lengths of the perpendiculars from Z' upon PQ and RS are of opposite symbols. Now, if Z'W ⊥ PQ and Z'C ⊥ RS then it readily follows that Z'W = -Z'C

⇒ $\frac{a_{1}α + b_{1}β + c_{1}}{\sqrt{a_{1}^{2} + b_{1}^{2}}}$ = - $\frac{a_{2}α + b_{2}β + c_{2}}{\sqrt{a_{2}^{2} + b_{2}^{2}}}$ 

Therefore, the equation to the locus of Z' (α, β) is

$\frac{a_{1}x + b_{1}y + c_{1}}{\sqrt{a_{1}^{2} + b_{1}^{2}}}$ = - $\frac{a_{2}x + b_{2}y + c_{2}}{\sqrt{a_{2}^{2} + b_{2}^{2}}}$ ………… (ii), which is the equation of the bisector of the angle not containing the origin.

From (i) and (ii) it is seen that the equations of the bisectors of the angles between the lines a$_{1}$x + b$_{1}$y + c$_{1}$ = 0 and a$_{2}$x + b$_{2}$y + c$_{2}$ = 0 are $\frac{a_{1}x + b_{1}y + c_{1}}{\sqrt{a_{1}^{2} + b_{1}^{2}}}$ = ±$\frac{a_{2}x + b_{2}y + c_{2}}{\sqrt{a_{2}^{2} + b_{2}^{2}}}$.

Note: The bisectors (i) and (ii) are perpendicular to each other.

Algorithm to find the bisectors of acute and obtuse angles between two lines:

Let the equations of the two lines be a$_{1}$x + b$_{1}$y + c$_{1}$ = 0 and a$_{2}$x + b$_{2}$y + c$_{2}$ = 0. To separate the bisectors of the obtuse and acute angles between the lines we proceed as follows:

Step I: First check whether the constant terms c$_{1}$ and c$_{2}$ in the two equations are positive or not. Suppose not, then multiply both the sides of the given equations by -1 to make the constant terms positive.

Step II: Determine the symbols of the expression a$_{1}$a$_{2}$ + b$_{1}$b$_{2}$.

Step III: If a$_{1}$a$_{2}$ + b$_{1}$b$_{2}$ > 0, then the bisector corresponding to “ + “ symbol gives the obtuse angle bisector and the bisector corresponding to “ - “ is the bisector of the acute angle between the lines i.e.

$\frac{a_{1}x + b_{1}y + c_{1}}{\sqrt{a_{1}^{2} + b_{1}^{2}}}$ = + $\frac{a_{2}x + b_{2}y + c_{2}}{\sqrt{a_{2}^{2} + b_{2}^{2}}}$ and $\frac{a_{1}x + b_{1}y + c_{1}}{\sqrt{a_{1}^{2} + b_{1}^{2}}}$ = - $\frac{a_{2}x + b_{2}y + c_{2}}{\sqrt{a_{2}^{2} + b_{2}^{2}}}$

are the bisectors of obtuse and acute angles respectively.

If a$_{1}$a$_{2}$ + b$_{1}$b$_{2}$ < 0, then the bisector corresponding to “ + “ and “ - “ symbol give the acute and obtuse angle bisectors respectively i.e.

$\frac{a_{1}x + b_{1}y + c_{1}}{\sqrt{a_{1}^{2} + b_{1}^{2}}}$ = + $\frac{a_{2}x + b_{2}y + c_{2}}{\sqrt{a_{2}^{2} + b_{2}^{2}}}$ and $\frac{a_{1}x + b_{1}y + c_{1}}{\sqrt{a_{1}^{2} + b_{1}^{2}}}$ = - $\frac{a_{2}x + b_{2}y + c_{2}}{\sqrt{a_{2}^{2} + b_{2}^{2}}}$

are the bisectors of acute and obtuse angles respectively.

Solved examples to find the equations of the bisectors of the angles between two given straight lines:

1. Find the equations of the bisectors of the angles between the straight lines 4x - 3y + 4 = 0 and 6x + 8y - 9 = 0.

Solution:

The equations of the bisectors of the angles between 4x - 3y + 4 = 0 and 6x + 8y - 9 = 0 are

$\frac{4x - 3y + 4}{\sqrt{4^2} + (-3)^{2}}$ = ± $\frac{6x + 8y - 9}{\sqrt{6^2} + 8^{2}}$

⇒ $\frac{4x - 3y + 4}{5}$ = ±$\frac{6x + 8y - 9}{10}$

⇒ 40x - 30y + 40 = ±(30x + 40y - 45)

Taking positive sign, we get,

⇒ 40x - 30y + 40 = +(30x + 40y - 45)

⇒ 2x - 14y + 17 = 0

Taking negative sign, we get,

⇒ 40x - 30y + 40 = -(30x + 40y - 45)

⇒ 40x - 30y + 40 = -30x - 40y + 45

⇒ 70x + 10y - 5 = 0

Therefore the equations of the bisectors of the angles between the straight lines 4x - 3y + 4 = 0 and 6x + 8y - 9 = 0 are 2x - 14y + 17 = 0 and 70x + 10y - 5 = 0.

2. Find the equation of the obtuse angle bisector of lines 4x - 3y + 10 = 0 and 8y - 6x - 5 = 0.

Solution:

First we make the constant terms positive in the given two equations.

Making positive terms positive, the two equations becomes

4x - 3y + 10 = 0 and 6x - 8y + 5 = 0

Now, a$_{1}$a$_{2}$ + b$_{1}$b$_{2}$ = 4 × 6 + (-3) × (-8) = 24 + 24 = 48, which is positive. Hence, “+” symbol gives the obtuse angle bisector. The obtuse angle bisector is

⇒ $\frac{4x - 3y + 10}{\sqrt{4^2} + (-3)^{2}}$ = + $\frac{6x - 8y + 5}{\sqrt{6^2} + (-8)^{2}}$

⇒ $\frac{4x - 3y + 10}{5}$ = +$\frac{6x - 8y + 5}{10}$

⇒ 40x - 30y + 100 = 30x - 40y - 50

⇒ 10x + 10y + 150 = 0

x + y + 15 = 0, which is the required obtuse angle bisector.

● The Straight Line

• Straight Line
• Slope of a Straight Line
• Slope of a Line through Two Given Points
• Collinearity of Three Points
• Equation of a Line Parallel to x-axis
• Equation of a Line Parallel to y-axis
• Slope-intercept Form
• Point-slope Form
• Straight line in Two-point Form
• Straight Line in Intercept Form
• Straight Line in Normal Form
• General Form into Slope-intercept Form
• General Form into Intercept Form
• General Form into Normal Form
  
• Point of Intersection of Two Lines
  
• Concurrency of Three Lines
• Angle between Two Straight Lines
• Condition of Parallelism of Lines
• Equation of a Line Parallel to a Line
• Condition of Perpendicularity of Two Lines
• Equation of a Line Perpendicular to a Line
• Identical Straight Lines
• Position of a Point Relative to a Line
• Distance of a Point from a Straight Line
• Equations of the Bisectors of the Angles between Two Straight Lines
• Bisector of the Angle which Contains the Origin
• Straight Line Formulae
• Problems on Straight Lines
• Word Problems on Straight Lines
• Problems on Slope and Intercept

11 and 12 Grade Math

From Equations of the Bisectors of the Angles between Two Straight Lines to HOME PAGE