Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Constructing a Line Segment
We will discuss here about constructing a line segment.
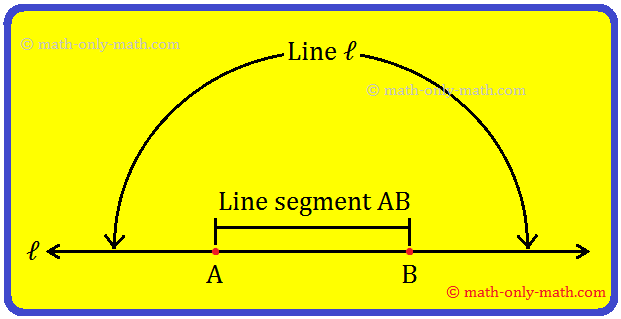
Since a line extends indefinitely in both the directions, it cannot be drawn completely. The arrowheads indicate that the line does not end on either side. If we mark two points, say A and B, on the line ℓ as shown in the following figure, then the portion of the line ℓ from A to B is called the line segment AB.
A and B are called its two end-points.
The line segment AB is written as AB or BA.
Line segment AB is represented as given below:
I: Construction of a Line Segment of the Given Length by Using Ruler/Scale:
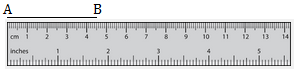
1. We know how to draw a line segment of a certain length. Suppose we want to draw a line segment of 4.5 cm length (say) using a scalce, we proceed as follows:
We follow the following steps as given below:
Step I: We place a scale on a paper sheet as shown below.
Step II: We place the sharp point of a pencil on the point which coincides with 0 on the scale and name it as A.
Step III: We mark another point B which coincides with the fifth millimetre division after the 4th centimetre. (1 small division = 1 mm.)
Step IV: We join both points A and B by drawing a line segment with a fine pointed pencil. The line segment AB is of 4.5 cm length.
Drawing a Line Segment:
2. Now, let us learn how to draw a line segment of a given length.
Step I: Place the ruler on the paper. Then mark two points P and Q against the marks 0 and 9 of the scale.
Step II: Keeping the scale evenly, move the pencil from P to Q along the edge of the scale. The line segment PQ is of length 9 cm.
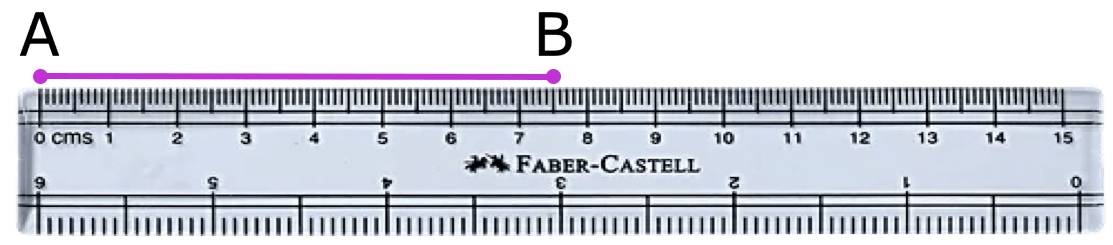
3. Suppose you have to draw a line segment AB of length 7.7 cm.
Place the ruler on the paper.
Mark a point against the ‘0’ mark and another point against 7.7 cm mark.
Join the points by pressing the scale evenly and moving the tip of the sharp pencil along the edge of the scale.
Remove the scale and name the points as A and B.
The line segment drawn is of 7.7 cm.
Methods to Draw a Line Segment:
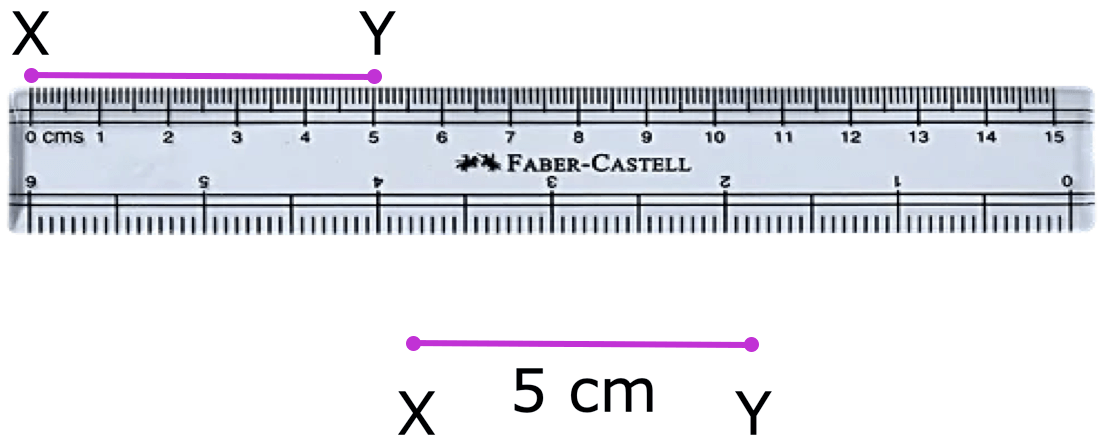
4. To draw a line segment of length 5 cm.
Step I. Take a pencil and a scale.
Step II. Put the scale on a sheet of paper and hold it firmly.
Step III. With the help of a sharp pencil, mark a point X against the 0 mark and a point Y against the 5 cm mark of the scale.
Step IV. Join the points X and Y.
Thus, we obtain the line segment XY of length 5 cm.
II: Construction of a Line Segment of the Given Length by Using Ruler/Scale and Compasses:
To draw a line segment of length 3.5 cm (say), using a scale and compass, we proceed as follows:
Working Rules for Construction of a Line Segment:
Step I: Draw a line 'ℓ' and mark a point P on it as shown in the figure.
Step II: Open the arms of either a divider or a compass, such that the end-points of the two arms opened equal to 3.5 cm, as shown in the figure.
Step III: Keeping the opening of the compass undisturbed, place it along the line 'ℓ such that its pointer-end coincides with the point P.
Step IV: Make a stroke with the pencil-end on the line 'ℓ to cut it at Q. as shown in the following figure.
This gives us the required line segment of length 3.5 cm i.e., PQ = 3.5 cm.
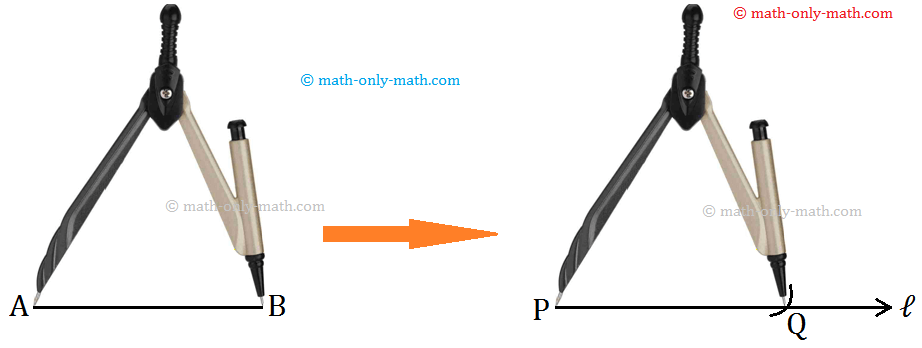
III: Constructing a Copy of a Given Line Segment (Say AB):
Suppose, you are given a line segment AB. You want to draw a line segment OC whose length is equal to AB.
Working Rules for Constructing a Copy of a Given Line Segment:
Step I: Fix your compass on AB such that the pointer is on A and the pencil-end is on B. Now, the opening of the compass given the length of \(\overline{AB}\).
Step II: Take out the compass undisturbed.
Step III: Draw any line 'ℓ' and mark a point O on it.
Step IV: Now, put the pointer of the compass on O and cut an arc that cuts the line 'ℓ' at a point C (say). Now, OC is the copy of AB.
IV: Construction of Line Segment Equal in Length to The Sum of The Lengths of Two Given Line Segments:
There are given two line segments PQ and ST. Construct a line segment equal to PQ + ST.
Working Rules:
Steps of Construction:
Step I: Draw any line p and mark a point O on it.
Step II: Construct a line segment OM on p equal in length to PQ starting from O.
Step III: Construct another segment ML on p equal in length to ST starting from M.
Now, OL is the required line segment equal to PQ + ST.
V: Construction of A Line Segment Equal In Length To The Difference of The Lengths of Two Given Line Segments:
Construct a line segment whose length is equal to the difference of two given line segments PQ and ST, i.e., PQ - ST when PQ > ST.
Working Rules:
Steps of Construction:
Step I: Draw any line p and mark a point O on it.
Step II: Construct a line segment OM on line p equal in length to PQ starting from O.
Step III: Construct another line segment ML on line p equal in length to ST but on the left of M i.e., L is between O and M.
Now, OL is the required line segment equal to PQ - ST.
Solved Examples on Constructing a Line Segment:
1. Construct any line segment \(\overline{AB}\), Without measuring it, construct a copy \(\overline{PQ}\) of \(\overline{AB}\)
Solution: First, draw AB of any measure. Then, draw a copy \(\overline{PQ}\) of \(\overline{AB}\) as shown below.
Worksheet on Constructing a Line Segment:
1. Draw line segments of the following
lengths using the ruler:
(i) 9 cm
(ii) 3 cm
(iii) 10 cm
(iv) 5 cm
(v) 7 cm
2. Draw two lines segments PQ and QR of length 4 cm each such that they meet at point Q. Measure the length of line segment PR.
3. Draw a line segment of length 5.8 cm using a scale/ruler only.
4. Construct three line segments of 6.5 cm, 7.7 cm and 9.2 cm, using ruler and compass only.
5. Construct any line segment \(\overline{XY}\). Without measuring it, construct a copy \(\overline{AB}\) of \(\overline{XY}\)
6. Construct two line segments of 3.6 cm and 7.5 cm using ruler and compass only.
7. Construct any line segment \(\overline{LM}\) . Without measuring it, construct a line segment \(\overline{XY}\) such that \(\overline{XY}\) is half of \(\overline{LM}\).
8. Construct any line segment \(\overline{AB}\). Without measuring it, copy it and construct another line segment \(\overline{PQ}\) such that \(\overline{PQ}\) = 3 \(\overline{AB}\).
9. PQ = 6.8 cm ST = 3.4 cm construct the following:
(i) PQ + ST
(ii) PQ - ST
(iii) PQ - \(\frac{1}{2}\)ST
10. Do the following:
(i) Draw a line segment that measures 8 cm.
(ii) Draw a line segment that measures 7 cm.
(iii) Draw a horizontal line segment of 6 cm and a vertical line segment of 6 cm so that they intersect each other. Name the line segments and the point of intersection.
From Constructing a Line Segment to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.



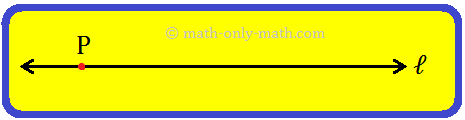




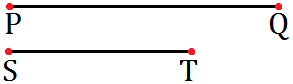

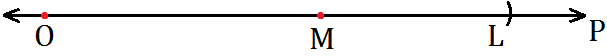
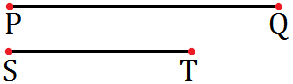


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.