Trigonometrical Ratios of (90° + θ)

What is the relation among all the trigonometrical ratios of (90° + θ)?

In trigonometrical ratios of angles (90° + θ) we will find the relation between all six trigonometrical ratios.

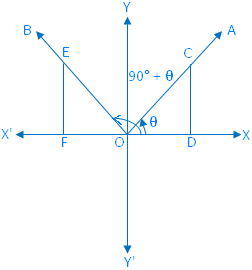
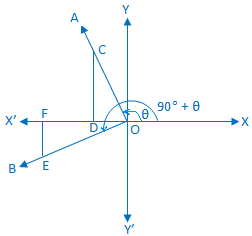
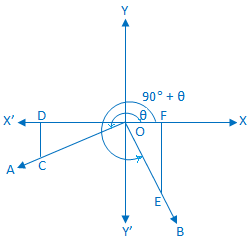
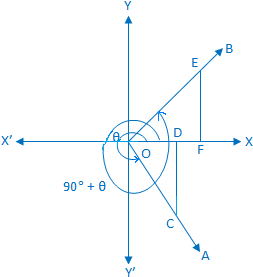
Let a rotating line OA rotates about O in the anti-clockwise direction, from initial position to ending position makes an angle ∠XOA = θ again the same rotating line rotates in the same direction and makes an angle ∠AOB =90°.

Therefore we see that, ∠XOB = 90° + θ. 

Take a point C on OA and draw CD perpendicular to OX or OX’.

Again, take a point E on OB such that OE = OC and draw EF perpendicular to OX or OX’. From the right-angled ∆ OCD and ∆ OEF we get,

∠COD = ∠OEF [since OB ⊥ OA]

and OC = OE.

Therefore, ∆ OCD ≅ ∆ OEF (congruent).

Therefore according to the definition of trigonometric sign, OF = - DC, FE = OD and OE = OC

We observe that in diagram 1 and 4 OF and DC are opposite signs and FE, OD are either both positive. Again we observe that in diagram 2 and 3 OF and DC are opposite signs and FE, OD are both negative.

According to the definition of trigonometric ratio we get,

sin (90° + θ) = \(\frac{FE}{OE}\)

sin (90° + θ) = \(\frac{OD}{OC}\), [FE = OD and OE = OC, since ∆ OCD ≅ ∆ OEF]

sin (90° + θ) = cos θ

cos (90° + θ) = \(\frac{OF}{OE}\)

cos (90° + θ) = \(\frac{- DC}{OC}\), [OF = -DC and OE = OC, since ∆ OCD ≅ ∆ OEF]

cos (90° + θ) = - sin θ.

tan (90° + θ) = \(\frac{FE}{OF}\)

tan (90° + θ) = \(\frac{OD}{- DC}\), [FE = OD and OF = - DC, since ∆ OCD ≅ ∆ OEF]

tan (90° + θ) = - cot θ.

Similarly, csc (90° + θ) = \(\frac{1}{sin (90° + \Theta)}\)

csc (90° + θ) =  \(\frac{1}{cos \Theta}\)

csc (90° + θ) = sec θ.

sec (90° + θ) = \(\frac{1}{cos (90° + \Theta)}\) 

sec (90° + θ) =  \(\frac{1}{- sin \Theta}\)

sec (90° + θ) = - csc θ.

and cot (90° + θ) = \(\frac{1}{tan (90° + \Theta)}\)

cot (90° + θ) = \(\frac{1}{- cot \Theta}\)

cot (90° + θ) = - tan θ.

Solved examples:

1. Find the value of sin 135°.

Solution:

sin 135° = sin (90 + 45)°

            = cos 45°; since we know, sin (90° + θ) = cos θ

            = \(\frac{1}{√2}\)

2. Find the value of tan 150°.

Solution:

tan 150° = tan (90 + 60)°

            = - cot 60°; since we know, tan (90° + θ) = - cot θ

            = \(\frac{1}{√3}\)

● Trigonometric Functions

• Basic Trigonometric Ratios and Their Names
• Restrictions of Trigonometrical Ratios
• Reciprocal Relations of Trigonometric Ratios
• Quotient Relations of Trigonometric Ratios
  
• Limit of Trigonometric Ratios
  
• Trigonometrical Identity
• Problems on Trigonometric Identities
• Elimination of Trigonometric Ratios
• Eliminate Theta between the equations
• Problems on Eliminate Theta
• Trig Ratio Problems
• Proving Trigonometric Ratios
• Trig Ratios Proving Problems
• Verify Trigonometric Identities
• Trigonometrical Ratios of 0°
• Trigonometrical Ratios of 30°
• Trigonometrical Ratios of 45°
• Trigonometrical Ratios of 60°
• Trigonometrical Ratios of 90°
• Trigonometrical Ratios Table
• Problems on Trigonometric Ratio of Standard Angle
  
• Trigonometrical Ratios of Complementary Angles
• Rules of Trigonometric Signs
• Signs of Trigonometrical Ratios
  
• All Sin Tan Cos Rule
• Trigonometrical Ratios of (- θ)
• Trigonometrical Ratios of (90° + θ)
• Trigonometrical Ratios of (90° - θ)
• Trigonometrical Ratios of (180° + θ)
• Trigonometrical Ratios of (180° - θ)
• Trigonometrical Ratios of (270° + θ)
• Trigonometrical Ratios of (270° - θ)
• Trigonometrical Ratios of (360° + θ)
• Trigonometrical Ratios of (360° - θ)
• Trigonometrical Ratios of any Angle
• Trigonometrical Ratios of some Particular Angles
• Trigonometric Ratios of an Angle
• Trigonometric Functions of any Angles
• Problems on Trigonometric Ratios of an Angle
• Problems on Signs of Trigonometrical Ratios

11 and 12 Grade Math

From Trigonometrical Ratios of (90° + θ) to HOME PAGE