Subscribe to our YouTube channel for the latest videos, updates, and tips.


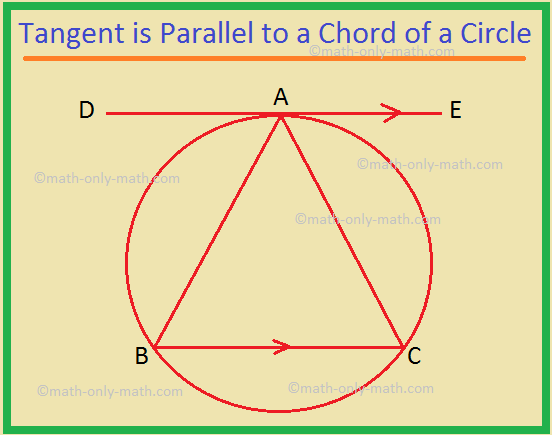
Tangent is Parallel to a Chord of a Circle

We will prove that, A tangent, DE, to a circle at A is parallel to a chord BC of the circle. Prove that A is equidistant from the extremities of the chord.

Tangent is Parallel to a Chord of a Circle

Solution:

Proof:

Statement

Reason

1. ∠DAB = ∠ACB

1. Angle between tangent and chord is equal to the angle in the alternate segment.

2. ∠DAB = ∠ABC

2. Alternate angles and DE  ∥ BC.

3. ∠ACB = ∠ABC

3. From statements 1 and 2.

4. AB = AC

⟹ A is equidistant from B and C, the extremities of the chord. (Proved)

4. From statement 3.







10th Grade Math

From Tangent is Parallel to a Chord of a Circle to HOME PAGE




Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.



New! Comments

Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.




Share this page: What’s this?

Recent Articles

RSS

  1. Worksheet on Rounding Decimals | Questions Related to Round a Decimal

    May 14, 25 04:21 PM

    The worksheet on rounding decimals would be really good for the students to practice huge number of questions related to round a decimal. This worksheet include questions related

    Read More

  2. Rounding Decimals | How to Round a Decimal? | Rounding off Decimal

    May 14, 25 03:01 PM

    Rounding decimals are frequently used in our daily life mainly for calculating the cost of the items. In mathematics rounding off decimal is a technique used to estimate or to find the approximate

    Read More

  3. Worksheet on Rounding Off Number | Rounding off Number | Nearest 10

    May 14, 25 12:50 PM

    In worksheet on rounding off number we will solve 10 different types of problems. 1. Round off to nearest 10 each of the following numbers: (a) 14 (b) 57 (c) 61 (d) 819 (e) 7729 2. Round off to

    Read More

  4. Rounding Off to the Nearest Whole Number | Nearest 10, 100, and 1000

    May 13, 25 03:43 PM

    Nearest Ten
    Here we will learn how to rounding off to the nearest whole number?

    Read More

  5. Conversion of Improper Fractions into Mixed Fractions |Solved Examples

    May 12, 25 04:52 AM

    Conversion of Improper Fractions into Mixed Fractions
    In conversion of improper fractions into mixed fractions, we follow the following steps: Step I: Obtain the improper fraction. Step II: Divide the numerator by the denominator and obtain the quotient…

    Read More