Straight Line in Intercept Form
We will learn how to find the equation of a straight line in intercept form.
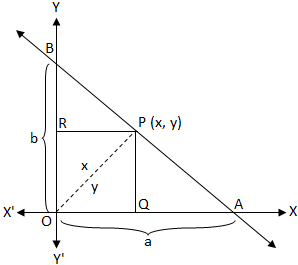
The equation of a line which cuts off intercepts a and b respectively from the x and y axes is xa + yb = 1.
Let the straight line AB intersects the x-axis at A and the y-axis at B where OA = a and OB = b.
Now we have to find the equation of the straight line AB.
Let P(x, y) be any point on the line AB. Draw PQ perpendicular on OX and PR perpendicular on OX. Then,
join the points O and P. Now, PQ = y, OQ = x.
Clearly, we see that
Area of the ∆OAB = Area of the ∆OPA + Area of the ∆OPB
⇒ ½ OA ∙ OB = ½ ∙ OA ∙ PQ + ½ ∙ OB ∙ PR
⇒ ½ a ∙ b = ½ ∙ a ∙ y + ½ ∙ b ∙ x
⇒ ab = ay + bx
⇒ abab = ay+bxab, dividing both sides by ab
⇒ 1 = ayab + bxab
⇒ 1 = yb + xa
⇒ xa + yb = 1, which is the equation of the line in the intercept form.
The equation xa + yb = 1 is the satisfied by the co-ordinates of any point P lying on the line AB.
Therefore, xa + yb = 1 represent the equation of the straight line AB.
Solved examples to find the equation of a straight line in intercept form:
1. Find the equation of the line which cuts off an intercept 3 on the positive direction of x-axis and an intercept 5 on the negative direction of y-axis.
Solution:
The equation of a line which cuts off intercepts a and b respectively from the x and y axes is xa + yb = 1.
Here, a = 3 and b = -5
Therefore, the equation of the straight line is xa + yb = 1 ⇒ x3 + y−5 = 1 ⇒ x3 - y5 = 1 ⇒ 5x – 3y = 15 ⇒ 5x – 3y – 15 = 0.
2. Find the intercepts of the straight line 4x + 3y = 24 on the co-ordinate axes.
Solution:
Given equation 4x + 3y = 24.
Now convert the given equation into intercept form.
4x + 3y = 24
⇒ 4x+3y24 = 2424, Dividing both sides by 24
⇒ 4x24 + 3y24 = 1
⇒ x6 + y8 = 1, which is the intercept form.
Therefore, x-intercept = 6 and y-intercept = 8.
Note: (i) The straight line xa + yb = 1 intersects the x-axis at A(a, 0) and the y-axis at B(0, b).
(ii) In xa + yb = 1, a is x-intercept and b is y- intercept.
These intercept a and b may be positive as well as negative.
(iii) If the straight line AB passing through the origin then, a = 0 and b = 0. If we put a = 0 and b = 0 in the intercept form, then x0 + y0 = 1, which is undefined. For this reason the equation of a straight line passing through the origin cannot be expressed in the intercept form.
(iv) A line parallel to the x-axis does not intercept the x-axis at any finite distance and hence, we cannot get any finite x- intercept (i.e., a) of such a line. For this reason, a line parallel to x-axis cannot be expressed in the intercept from. In like manner, we cannot get any finite y- intercept (i.e., b) of a line parallel to y-axis and hence, such a line cannot be expressed in the intercept form.
● The Straight Line
- Straight Line
- Slope of a Straight Line
- Slope of a Line through Two Given Points
- Collinearity of Three Points
- Equation of a Line Parallel to x-axis
- Equation of a Line Parallel to y-axis
- Slope-intercept Form
- Point-slope Form
- Straight line in Two-point Form
- Straight Line in Intercept Form
- Straight Line in Normal Form
- General Form into Slope-intercept Form
- General Form into Intercept Form
- General Form into Normal Form
- Point of Intersection of Two Lines
- Concurrency of Three Lines
- Angle between Two Straight Lines
- Condition of Parallelism of Lines
- Equation of a Line Parallel to a Line
- Condition of Perpendicularity of Two Lines
- Equation of a Line Perpendicular to a Line
- Identical Straight Lines
- Position of a Point Relative to a Line
- Distance of a Point from a Straight Line
- Equations of the Bisectors of the Angles between Two Straight Lines
- Bisector of the Angle which Contains the Origin
- Straight Line Formulae
- Problems on Straight Lines
- Word Problems on Straight Lines
- Problems on Slope and Intercept
11 and 12 Grade Math
From Straight Line in Intercept Form to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Expanded Form of a Number | Writing Numbers in Expanded Form | Values
Apr 27, 25 10:13 AM
We know that the number written as sum of the place-values of its digits is called the expanded form of a number. In expanded form of a number, the number is shown according to the place values of its… -
Converting Fractions to Decimals | Solved Examples | Free Worksheet
Apr 26, 25 05:04 PM
In converting fractions to decimals, we know that decimals are fractions with denominators 10, 100, 1000 etc. In order to convert other fractions into decimals, we follow the following steps: -
Converting Decimals to Fractions | Solved Examples | Free Worksheet
Apr 26, 25 04:56 PM
In converting decimals to fractions, we know that a decimal can always be converted into a fraction by using the following steps: Step I: Obtain the decimal. Step II: Remove the decimal points from th… -
Worksheet on Decimal Numbers | Decimals Number Concepts | Answers
Apr 26, 25 03:48 PM
Practice different types of math questions given in the worksheet on decimal numbers, these math problems will help the students to review decimals number concepts. -
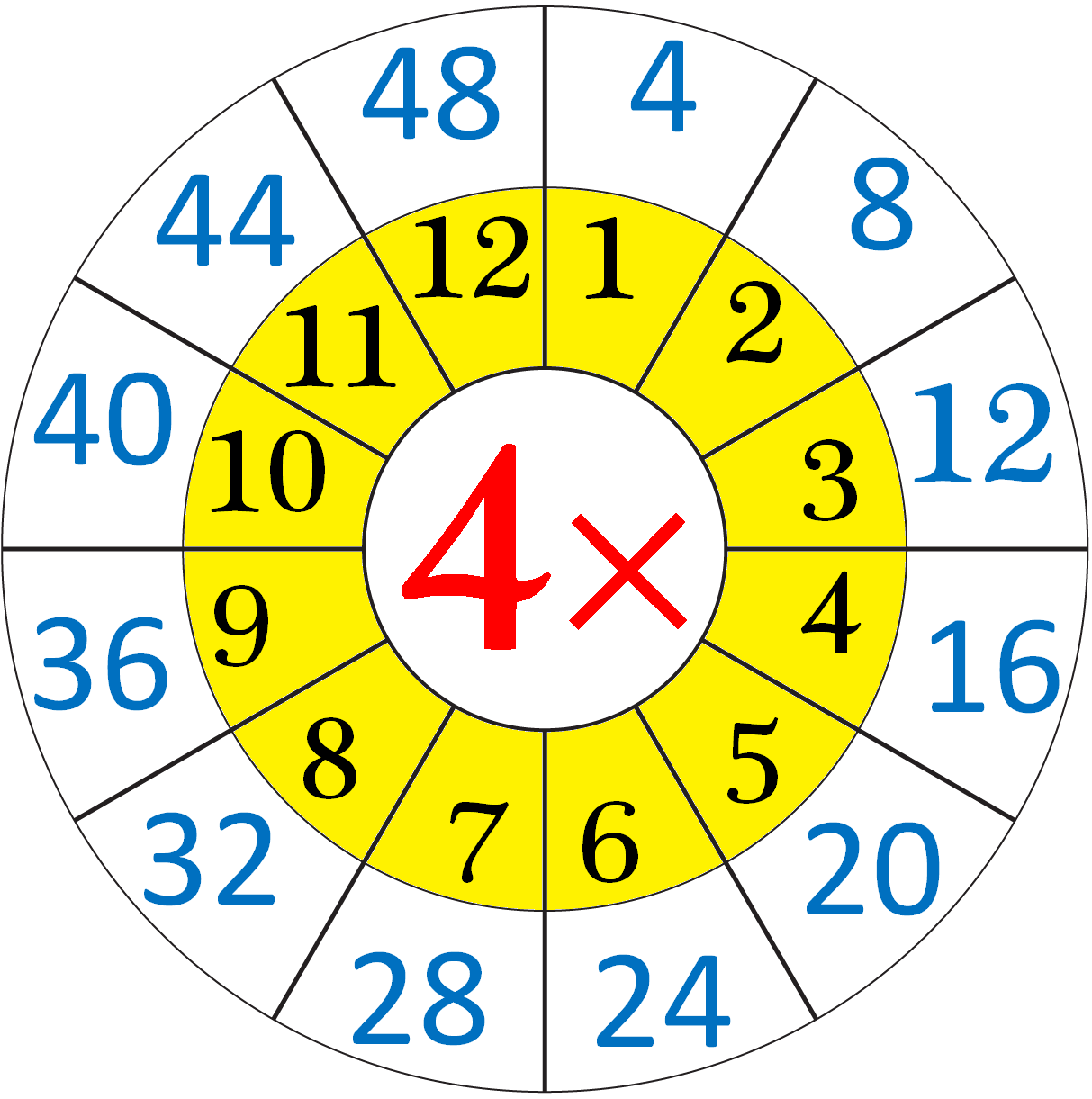
Multiplication Table of 4 |Read and Write the Table of 4|4 Times Table
Apr 26, 25 01:00 PM
Repeated addition by 4’s means the multiplication table of 4. (i) When 5 candle-stands having four candles each. By repeated addition we can show 4 + 4 + 4 + 4 + 4 = 20 Then, four 5 times



New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.