Straight Line Formulae
Straight line formulae will help us to solve different types of problems on straight line in co-ordinate geometry.
1. If a straight line makes an angle α with the positive direction of the x-axis then the slope or gradient of the line i.e. m = tan α.
2. Slope of the line joining the points (x1, y1) and (x2, y2) is
m = y2−y1x2−x1 = Difference of ordinates of the given pointDifference of abscissa of the given point
3. Condition of collinearity of three points (x1, y1), (x2, y2) and (x3, y3) is x1 (y2 - y3) + x2 (y3 - y1) + x3 (y1 - y2) = 0.
4. The equation of x-axis is y = 0.
5. The equation of y-axis is x = 0.
6. The
equation of the line parallel to x-axis at a distance h units from x-axis is, y
= h.
7. The equation of the line parallel to y-axis at a distance k units from y-axis is, x = k.
8. The equation of a straight line in slope-intercept form is y = mx + b, where m is the slope of the line and b is the y-intercept.
9. The equation of a straight line in point-slope form is y - y1 = m (x - x1) where m is the slope of the line and (x1, y1) is a given point on the line.
10.The equation of a straight line in symmetrical form is
x−x1cosθ = y−y1sinθ = r
Where θ is the inclination of the line, (x1, y1) is a given point on the line and r is the distance between the points (x, y) and (x1, y1).
11. The equation of a straight line in distance form is
x−x1cosθ = y−y1sinθ = r
Where θ is the inclination of the line, (x1, y1) is a given point on the line and r is the distance of the point (x, y) on the line from the point (x1, y1).
12. The equation of a straight line in two-point form is
y−y1x−x1 = y1−y2x1−x2 or, y - y1 = y2−y1x2−x1 (x - x1)
Where (x1, y1) and (x2, y2) are two given points on the line.
13. The equation of a straight line in intercept form is xa + yb = 1
Where a is the x-intercept and b is the y-intercept of the line. The straight line intersects the x-axis at (a, 0) and y-axis at (0, b).
14. The equation of a straight line in normal form is x cos α + y sin α = p where p (> 0) is the perpendicular distance of the line from the origin and a (0 ≤ α ≤ 2π) is the angle that the drawn perpendicular on the line makes with the positive direction of the x-axis.
15. The equation of a straight line in general form is ax + by + c = 0 where a, b and c are real constants (a and b both are not zero).
16. To find the co-ordinates of the point of intersection of two given lines we solve the equations; the value of x is the abscissa and that of y is the ordinate of the point of intersection.
17. The equation of any straight line through the point of intersection of the lines a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 is
a1x + b1y + c1 + λ (a2x + b2y + c2) = 0, where λ(≠ 0 or ∞) is an arbitrary constant.
18. Three given straight lines are concurrent if the point of intersection of any two of them satisfies the equation of the third straight line.
19. If θ be the acute angle between the straight lines y = m1x + c1 and y = m2x + c2 then,
tan θ = |m2−m11+m1m2| or, tan θ = ± m2−m11+m1m2
20. If two straight lines are parallel then their slopes would be equal. Thus, the condition of parallelism for the lines y = m1x+ c1 and y = m2x + c2 is, m1 = m2.
21. The equation of any straight line parallel to the line ax + by + c 0 is ax + by = k where k is an arbitrary constant.
22. Two straight lines are perpendicular to each other if the product of ,their slopes = – 1. Thus, the condition of perpendicularity of the lines y = m1x + c1 and y = m2x + c2 is m1 m2 = - 1.
23. The equation of any straight line perpendicular to the line ax + by + c = 0 is bx - ay = k where k is an arbitrary constant.
24. The two equations a1 x + b1 y + c1 = 0 and a2 x + b2y + c2 = 0 represent the equation of the same straight line when a1a2 = b1b2 = c1c2.
25. Let ax + by + c = 0 be a given straight line and P (x1, y1) and Q (x2, y2), two given points. The points P and Q are on the same side or opposite sides of the line ax + by + c = 0 according as (ax + by + c) and (ax1 + by1 + c) are of the same or opposite signs.
The origin and the point P (x1, y1) are on the same side or opposite sides of the straight line ax + by + c = 0 according as c and (ax1 + by1 + c) are of the same or opposite signs.
26. Let P (x1, y1) be a point not lying on the straight line ax + by + c = 0; then the length of the perpendicular drawn from P upon the line is
±a1x+b1y+c√a2+b2 or,|a1x+b1y+c|√a2+b2
27. The equations of the bisectors of the angles between the straight lines a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 are,
a1x+b1y+c1√a21+b21 = ±a2x+b2y+c2√a22+b22
If c1 and c2 are of the same signs then the bisector containing the origin is,
a1x+b1y+c1√a21+b21 = +a2x+b2y+c2√a22+b22.
If c1 and c2 are of opposite signs then the bisector containing the origin is,
a1x+b1y+c1√a21+b21 = -a2x+b2y+c2√a22+b22.
● The Straight Line
- Straight Line
- Slope of a Straight Line
- Slope of a Line through Two Given Points
- Collinearity of Three Points
- Equation of a Line Parallel to x-axis
- Equation of a Line Parallel to y-axis
- Slope-intercept Form
- Point-slope Form
- Straight line in Two-point Form
- Straight Line in Intercept Form
- Straight Line in Normal Form
- General Form into Slope-intercept Form
- General Form into Intercept Form
- General Form into Normal Form
- Point of Intersection of Two Lines
- Concurrency of Three Lines
- Angle between Two Straight Lines
- Condition of Parallelism of Lines
- Equation of a Line Parallel to a Line
- Condition of Perpendicularity of Two Lines
- Equation of a Line Perpendicular to a Line
- Identical Straight Lines
- Position of a Point Relative to a Line
- Distance of a Point from a Straight Line
- Equations of the Bisectors of the Angles between Two Straight Lines
- Bisector of the Angle which Contains the Origin
- Straight Line Formulae
- Problems on Straight Lines
- Word Problems on Straight Lines
- Problems on Slope and Intercept
11 and 12 Grade Math
From Straight Line Formulae to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
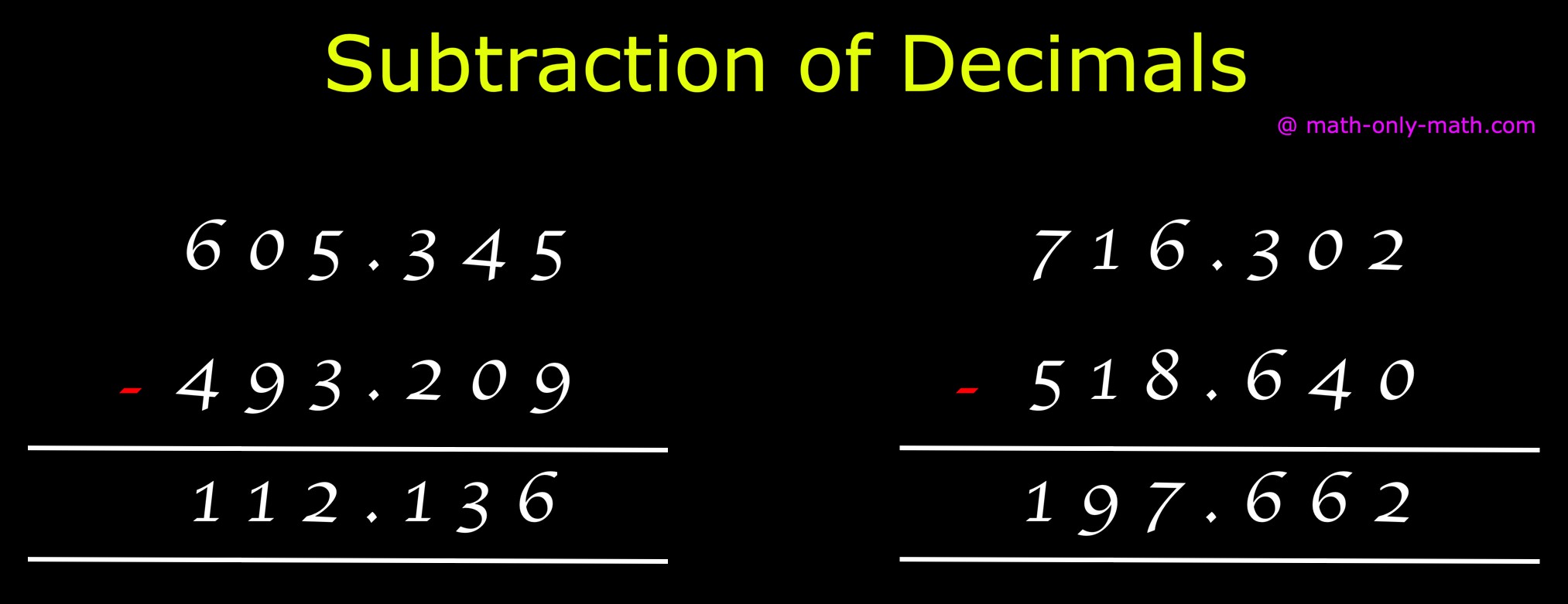
Subtraction of Decimals | Subtracting Decimals | Decimal Subtraction
Apr 24, 25 03:25 PM
We will discuss here about the subtraction of decimals. Decimals are subtracted in the same way as we subtract ordinary numbers. We arrange the digits in columns -
How to Do Long Division? | Method | Steps | Examples | Worksheets |Ans
Apr 24, 25 10:18 AM
As we know that the division is to distribute a given value or quantity into groups having equal values. In long division, values at the individual place (Thousands, Hundreds, Tens, Ones) are dividend… -
Division by Two-Digit Numbers | Knowledge of Estimation | Division
Apr 24, 25 10:12 AM
In division by two-digit numbers we will practice dividing two, three, four and five digits by two-digit numbers. Consider the following examples on division by two-digit numbers: Let us use our knowl… -
Addition of Decimals | How to Add Decimals? | Adding Decimals|Addition
Apr 24, 25 01:45 AM
We will discuss here about the addition of decimals. Decimals are added in the same way as we add ordinary numbers. We arrange the digits in columns and then add as required. Let us consider some -
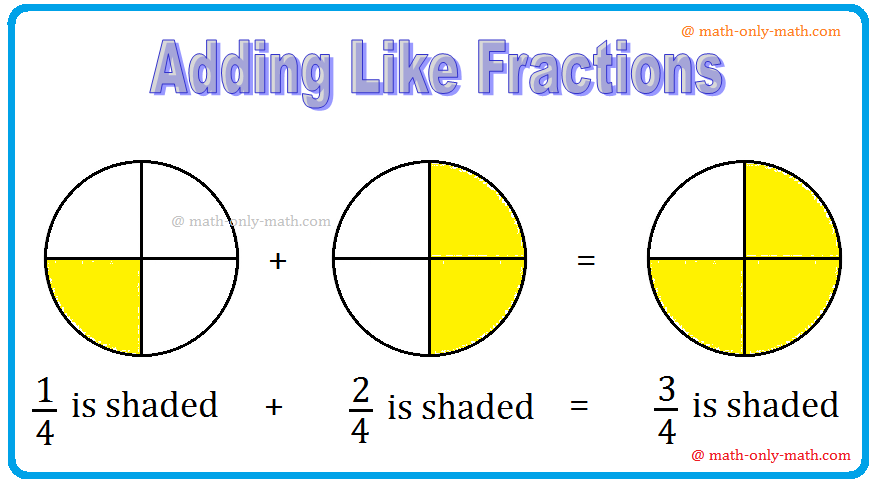
Addition of Like Fractions | Examples | Videos | Worksheet | Fractions
Apr 23, 25 09:23 AM
To add two or more like fractions we simplify add their numerators. The denominator remains same. Thus, to add the fractions with the same denominator, we simply add their numerators and write the com…




New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.