Standard Equation of a Parabola

We will discuss about the standard equation of a parabola.

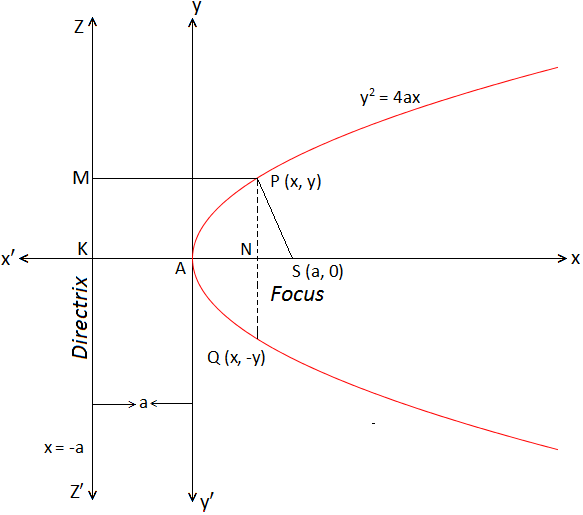
Let S be the focus and the straight line ZZ', the directrix of the required parabola.  Let SK be the straight line through S perpendicular to the directrix, bisect SK at A and K being the point of intersection with the directrix.

Then

AS = AK

⇒ Distance of A from the focus = Distance of A from the directrix

⇒ A lies on the parabola

Let SK = 2a, where, a > 0.

Then AS = AK = a.

If this line SK intersects the parabola at A then SK is the axis and A is the vertex of the parabola. Draw the straight line AY through A perpendicular to the axis. Now, we choose the origin of co-ordinates at A and x and y-axis along AS and AY respectively.

Let P (x, y) be any point on the required parabola. Join SP and draw PM and PN perpendicular to the directrix ZZ' and x-axis. Then,

PM = NK = AN + AK = x + a

Now, P lies on the parabola ⇒ SP = PM

⇒ SP\(^{2}\) = PM\(^{2}\)

⇒ (x – a)\(^{2}\) + (y – 0)\(^{2}\) = (x + a)\(^{2}\)

⇒ y\(^{2}\) = 4ax, which is the required equation of the parabola. The equation of a parabola in the form y\(^{2}\) = 4ax is known as the standard equation of a parabola.

Notes:

(i) The parabola has two real foci situated on its axis one of which is the focus S and the other lies at infinity. The corresponding directrix is also at infinity.

(ii) The vertex of the parabola y\(^{2}\) = 4ax is at the origin i.e., the co-ordinates of its vertex are (0, 0).

(iii) The co-ordinates of the focus S of the parabola y\(^{2}\) = 4ax are (a, 0).

(iv) The axis of the parabola y\(^{2}\) = 4ax is positive x-axis (assuming a> 0).

(v) The parabola is symmetric with respect to with respect to its axis. If the point P(x, y) lies on the parabola y\(^{2}\) = 4ax with respect to x-axis, then the point Q (x, -y) also lies on it.

(vi) We have, y\(^{2}\) = 0 when x = 0; hence, the straight line x = 0 (i.e., y-axis) intersects the parabola y\(^{2}\) = 4ax at coincident points. Therefore, y-axis is a tangent to the parabola y\(^{2}\) = 4ax at the origin.

(vii) The line segment PQ is the double ordinate of P and PQ = 2y.

(viii) The co-ordinates of the end points of the latus rectum L\(_{1}\)L\(_{2}\) of the parabola y\(^{2}\) = 4ax are (a, 2a) and (a, -2a) respectively

(ix) The length of the latus rectum of the parabola y\(^{2}\) = 4ax is 4a.

(ix) The equation of the directrix of the parabola y\(^{2}\) = 4ax is x = - a ⇒ x + a = 0.

(x) The directrix of the parabola y\(^{2}\) = 4ax is parallel to y-axis and it passes through the point K (- a, 0).

(xi) x = at\(^{2}\), y = 2at is the parametric form of the parabola y\(^{2}\) = 4ax and t is called the parameter.

(xii) The co-ordinates of any point on the parabola y\(^{2}\) = 4ax can be represented as (at\(^{2}\), 2at) where (at\(^{2}\), 2at) are called the parametric co-ordinates of a point on the parabola y\(^{2}\) = 4ax.

(xiii) From the standard equation of the parabola y\(^{2}\) = 4ax we see that the value of y becomes imaginary when x < 0. Therefore, no portion of the parabola y\(^{2}\) = 4ax lies to the left of y-axis.

Again, if x is positive and gradually increases then y also increases and for each positive value of x we get two values of y which are equal and opposite in signs. Therefore, the curve extends to infinity on the right of the y-axis.

● The Parabola

• Concept of Parabola
• Standard Equation of a Parabola
• Standard form of Parabola y22 = - 4ax
• Standard form of Parabola x22 = 4ay
• Standard form of Parabola x22 = -4ay
• Parabola whose Vertex at a given Point and Axis is Parallel to x-axis
• Parabola whose Vertex at a given Point and Axis is Parallel to y-axis
• Position of a Point with respect to a Parabola
  
• Parametric Equations of a Parabola
• Parabola Formulae
• Problems on Parabola

11 and 12 Grade Math 

From Standard Equation of a Parabola to HOME PAGE