Projection Formulae

Projection formulae is the length of any side of a triangle is equal to the sum of the projections of other two sides on it.

In Any Triangle ABC,

(i) a = b cos C + c cos B

(ii)  b = c cos A + a cos C

(iii) c = a cos B +  b cos A

Proof:   

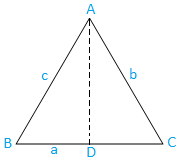
Let ABC be a triangle. Then the following three cases arises:

Case I: If ABC is an acute-angled triangle then we get,

           a = BC = BD + CD ………………………… (i)

Now from the triangle ABD we have, cos B = BD/AB    ⇒ BD = AB cos B ⇒ BD = c cos B, [since, AB = c] Again, cos C = CD/AC   ⇒ CD = AC cos C  ⇒ CD = b cos C, [since, AC = b]

Now, substitute the value of BD and CD in equation (i) we get,

        a = c cos B + b cos C         

Note: We observe in the above diagram BD and CD are projections of AB and AC respectively on BC.

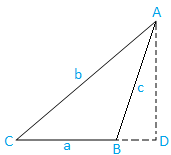
Case II: If ABC is an acute-angled triangle then we get,

            a = BC = CD - BD                                           ………………………… (ii)

Now from the triangle ADC we have, cos C =  CD/AC    ⇒ CD = AC cos C ⇒ CD = b cos C, [since, AC = b] Again, cos (π - B) = BD/AB   ⇒ BD = AB cos (π - B)

⇒ BD = -c cos B, [since, AB = c and cos (π - θ) = -cos θ]

Now, substitute the value of BD and CD in equation (ii) we get,

       a = b cos C - (-c cos B)

⇒ a = b cos C + c cos B

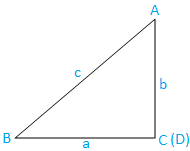
Case III: If ABC is a right-angled triangle then we get,

             a = BC                                              ………………………… (iii)

and cos B =  BC/AB    ⇒ BC = AB cos B ⇒ BC = c cos B, [since, AB = c] Now, substitute the value of BC in equation (iii) we get,        a = c cos B ⇒ a = c cos B + 0

⇒ a = c cos B + b cos C, [since C = 90° ⇒ cos C = cos 90 = 0] 

Therefore, in any triangle ABC we get, a = b cos C + c cos B

Similarly, we can prove that the formulae b = c cos A + a cos C and c = a cos B + b cos A.

Solved problem using the projection formulae:

If the area of the triangle ABC be ∆, show that,
                       b$^{2}$ sin 2C + c$^{2}$ sin 2B = 4∆.

Solution:

b$^{2}$ sin 2C + c$^{2}$ sin 2B

= b$^{2}$ 2 sin C cos C + c$^{2}$ ∙ 2 sin B cos B

= 2b cos C ∙ b sin C + 2c cos B ∙ c sin B

= 2b cos C ∙ c sin B + 2c cos B ∙ c sin B, [Since, a/sin B = c/sin C ⇒ b sin C = c sin B]

= 2c sin B (b cos C + c cos B)

= 2c sin B ∙ a [Since, we know that, a = b cos C + c cos B]

= 4 ∙ ½ ac sin B

= 4∆.                        Proved.

● Properties of Triangles

• The Law of Sines or The Sine Rule
• Theorem on Properties of Triangle
• Projection Formulae
• Proof of Projection Formulae
• The Law of Cosines or The Cosine Rule
  
• Area of a Triangle
• Law of Tangents
• Properties of Triangle Formulae
• Problems on Properties of Triangle

11 and 12 Grade Math

From Projection Formulae to HOME PAGE