Probability of Tossing Two Coins
Here we will learn how to find the probability of tossing two coins.
Let us take the experiment of tossing two coins simultaneously:
When we toss two coins simultaneously then the possible of outcomes are: (two heads) or (one head and one tail) or (two tails) i.e., in short (H, H) or (H, T) or (T, T) respectively; where H is denoted for head and T is denoted for tail.
Therefore, total numbers of outcome are 22 = 4The above explanation will help us to solve the problems on finding the probability of tossing two coins.
Worked-out problems on probability involving tossing or flipping two coins:
1. Two different coins are tossed randomly. Find the probability of:
(i) getting two heads
(ii) getting two tails
(iii) getting one tail
(iv) getting no head
(v) getting no tail
(vi) getting at least 1 head
(vii) getting at least 1 tail
(viii) getting atmost 1 tail
(ix) getting 1 head and 1 tail
Solution:
When two different coins are tossed randomly, the sample space is given by
S = {HH, HT, TH, TT}
Therefore, n(S) = 4.
(i) getting two heads:
Let E1 = event of getting 2 heads. Then,E1 = {HH} and, therefore, n(E1) = 1.
Therefore, P(getting 2 heads) = P(E1) = n(E1)/n(S) = 1/4.
(ii) getting two tails:
Let E2 = event of getting 2 tails. Then,E2 = {TT} and, therefore, n(E2) = 1.
Therefore, P(getting 2 tails) = P(E2) = n(E2)/n(S) = 1/4.
(iii) getting one tail:
Let E3 = event of getting 1 tail. Then,E3 = {TH, HT} and, therefore, n(E3) = 2.
Therefore, P(getting 1 tail) = P(E3) = n(E3)/n(S) = 2/4 = 1/2
(iv) getting no head:
Let E4 = event of getting no head. Then,E4 = {TT} and, therefore, n(E4) = 1.
Therefore, P(getting no head) = P(E4) = n(E4)/n(S) = ¼.
(v) getting no tail:
Let E5 = event of getting no tail. Then,E5 = {HH} and, therefore, n(E5) = 1.
Therefore, P(getting no tail) = P(E5) = n(E5)/n(S) = ¼.
(vi) getting at least 1 head:
Let E6 = event of getting at least 1 head. Then,E6 = {HT, TH, HH} and, therefore, n(E6) = 3.
Therefore, P(getting at least 1 head) = P(E6) = n(E6)/n(S) = ¾.
(vii) getting at least 1 tail:
Let E7 = event of getting at least 1 tail. Then,E7 = {TH, HT, TT} and, therefore, n(E7) = 3.
Therefore, P(getting at least 1 tail) = P(E2) = n(E2)/n(S) = ¾.
(viii) getting atmost 1 tail:
Let E8 = event of getting atmost 1 tail. Then,E8 = {TH, HT, HH} and, therefore, n(E8) = 3.
Therefore, P(getting atmost 1 tail) = P(E8) = n(E8)/n(S) = ¾.
(ix) getting 1 head and 1 tail:
Let E9 = event of getting 1 head and 1 tail. Then,E9 = {HT, TH } and, therefore, n(E9) = 2.
Therefore, P(getting 1 head and 1 tail) = P(E9) = n(E9)/n(S)= 2/4 = 1/2.
The solved examples involving probability of tossing two coins will help us to practice different questions provided in the sheets for flipping 2 coins.
Probability
Probability of Tossing Two Coins
Probability of Tossing Three Coins
Probability for Rolling Two Dice
Probability for Rolling Three Dice
From Probability of Tossing Two Coins to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
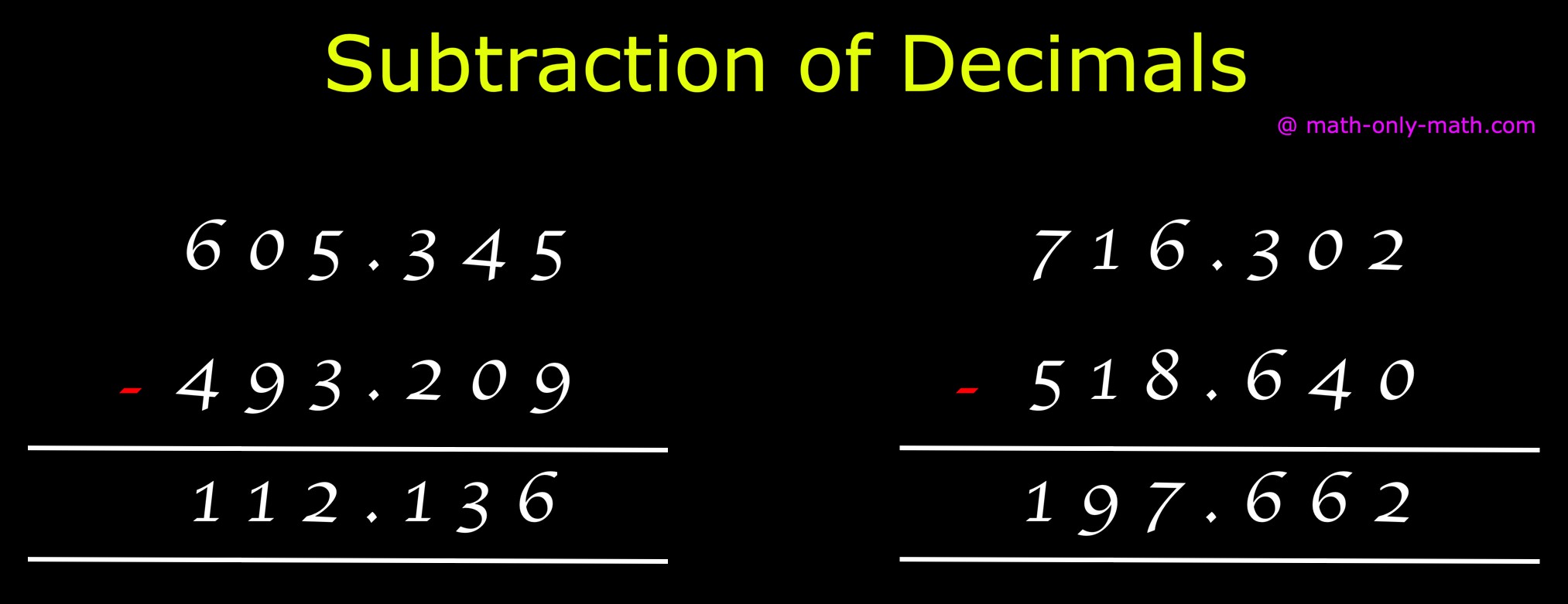
Subtraction of Decimals | Subtracting Decimals | Decimal Subtraction
Apr 24, 25 03:25 PM
We will discuss here about the subtraction of decimals. Decimals are subtracted in the same way as we subtract ordinary numbers. We arrange the digits in columns -
How to Do Long Division? | Method | Steps | Examples | Worksheets |Ans
Apr 24, 25 10:18 AM
As we know that the division is to distribute a given value or quantity into groups having equal values. In long division, values at the individual place (Thousands, Hundreds, Tens, Ones) are dividend… -
Division by Two-Digit Numbers | Knowledge of Estimation | Division
Apr 24, 25 10:12 AM
In division by two-digit numbers we will practice dividing two, three, four and five digits by two-digit numbers. Consider the following examples on division by two-digit numbers: Let us use our knowl… -
Addition of Decimals | How to Add Decimals? | Adding Decimals|Addition
Apr 24, 25 01:45 AM
We will discuss here about the addition of decimals. Decimals are added in the same way as we add ordinary numbers. We arrange the digits in columns and then add as required. Let us consider some -
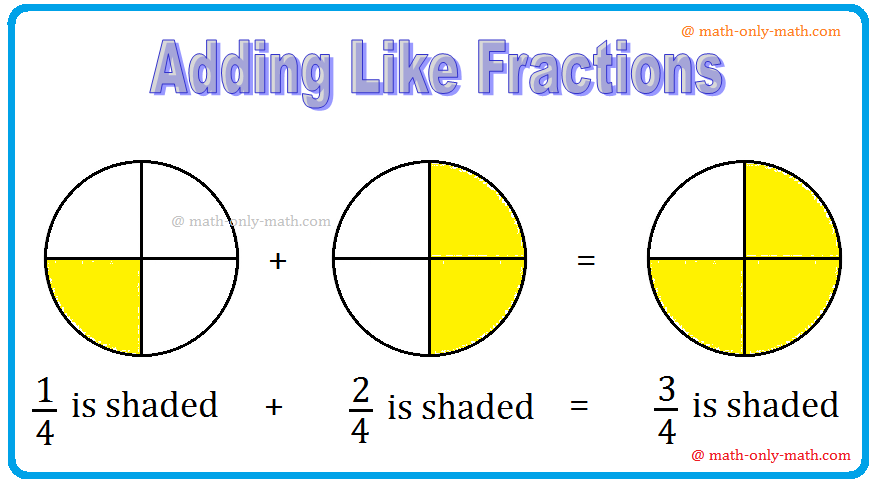
Addition of Like Fractions | Examples | Videos | Worksheet | Fractions
Apr 23, 25 09:23 AM
To add two or more like fractions we simplify add their numerators. The denominator remains same. Thus, to add the fractions with the same denominator, we simply add their numerators and write the com…




New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.