Position of a Point with respect to a Parabola

We will learn how to find the position of a point with respect to a parabola.

The position of a point (x\(_{1}\), y\(_{1}\)) with respect to a parabola y\(^{2}\) = 4ax (i.e. the point lies outside, on or within the parabola) according as y\(_{1}\)\(^{2}\) - 4ax\(_{1}\) >, =, or < 0.

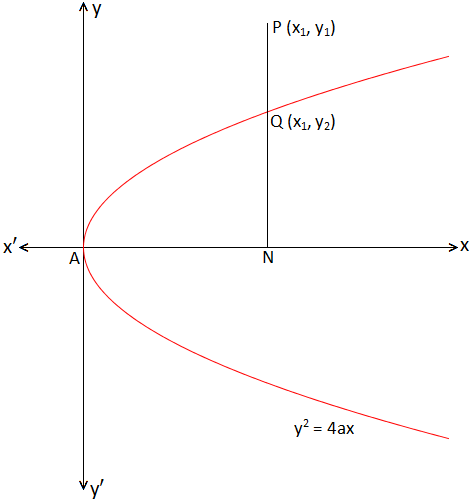
Let P(x\(_{1}\), y\(_{1}\)) be a point on the plane. From P draw PN perpendicular to the x-axis i.e., AX and N being the foot of the perpendicular.

PN intersect the parabola y\(^{2}\) = 4ax at Q and let the coordinates of Q be (x\(_{1}\), y\(_{2}\)). Now, the point Q (x\(_{1}\), y\(_{2}\)) lies on the parabola y\(^{2}\) = 4ax. Hence we get

y\(_{2}\)\(^{2}\) = 4ax\(_{1}\)

Therefore, the point

(i) P lies outside the parabola y\(^{2}\) = 4ax if PN > QN

i.e., PN\(^{2}\) > QN\(^{2}\)

⇒ y\(_{1}\)\(^{2}\) > y\(_{2}\)\(^{2}\)

⇒ y\(_{1}\)\(^{2}\) > 4ax\(_{1}\), [Since, 4ax\(_{1}\) = y\(_{2}\)\(^{2}\)].

(ii) P lies on the parabola y\(^{2}\) = 4ax if PN = QN

i.e., PN\(^{2}\) = QN\(^{2}\)

⇒ y\(_{1}\)\(^{2}\) = y\(_{2}\)\(^{2}\)

⇒ y\(_{1}\)\(^{2}\) = 4ax\(_{1}\), [Since, 4ax\(_{1}\) = y\(_{2}\)\(^{2}\)].

(iii) P lies outside the parabola y\(^{2}\) = 4ax if PN < QN

i.e., PN\(^{2}\) < QN\(^{2}\)

⇒ y\(_{1}\)\(^{2}\) < y\(_{2}\)\(^{2}\)

⇒ y\(_{1}\)\(^{2}\) < 4ax\(_{1}\), [Since, 4ax\(_{1}\) = y\(_{2}\)\(^{2}\)].

Therefore, the point P (x\(_{1}\), y\(_{1}\)) lies outside, on or within the parabola y\(^{2}\) = 4ax according as

y\(_{1}\)\(^{2}\) - 4ax\(_{1}\) >,= or < 0.

Notes:

(i) The point P(x\(_{1}\), y\(_{1}\)) lies outside, on or within the parabola y\(^{2}\) = -4ax according as y\(_{1}\)\(^{2}\) + 4ax\(_{1}\) >, = or <0.

(ii) The point P(x\(_{1}\), y\(_{1}\)) lies outside, on or within the parabola x\(^{2}\) = 4ay according as x\(_{1}\)\(^{2}\) - 4ay\(_{1}\) >, = or <0.

(ii) The point P(x\(_{1}\), y\(_{1}\)) lies outside, on or within the parabola x\(^{2}\) = -4ay according as x\(_{1}\)\(^{2}\) + 4ay\(_{1}\) >, = or <0.

Solved examples to find the position of the point P (x\(_{1}\), y\(_{1}\)) with respect to the parabola y\(^{2}\) =  4ax:

1. Does the point (-1, -5) lies outside, on or within the parabola y\(^{2}\) = 8x?

Solution:

We know that the point (x\(_{1}\), y\(_{1}\)) lies outside, on or within the parabola y\(^{2}\) = 4ax according as y\(_{1}\)\(^{2}\) - 4ax\(_{1}\) is positive, zero or negative.

Now, the equation of the given parabola is y\(^{2}\) = 8x ⇒ y\(^{2}\) - 8x= 0

Here x\(_{1}\) = -1 and y\(_{1}\) = -5

Now, y\(_{1}\)\(^{2}\) - 8x\(_{1}\)  = (-5)\(^{2}\) - 8 ∙ (-1) = 25 + 8 = 33 > 0

Therefore, the given point lies outside the given parabola.

 

2. Examine with reasons the validity of the following statement:

"The point (2, 3) lies outside the parabola y\(^{2}\) = 12x but the point (- 2, - 3) lies within it."

Solution:         

We know that the point (x\(_{1}\), y\(_{1}\)) lies outside, on or within the parabola y\(^{2}\) = 4ax according as y\(_{1}\)\(^{2}\) - 4ax\(_{1}\) is positive, zero or negative.

Now, the equation of the given parabola is y\(^{2}\) = 12x or, y\(^{2}\) - 12x = 0

For then point (2, 3):

Here x\(_{1}\) = 2 and y\(_{1}\) = 3

Now, y\(_{1}\)\(^{2}\) - 12x\(_{1}\) = 3\(^{2}\) – 12 ∙ 2 = 9 - 24 = -15 < 0

Hence, the point (2, 3) lies within the parabola y\(^{2}\) = 12x.

For then point (-2, -3):

Here x\(_{1}\) = -2 and y\(_{1}\) = -3

Now, y\(_{1}\)\(^{2}\) - 12x\(_{1}\) = (-3)\(^{2}\) – 12 ∙ (-2) = 9 + 24 = 33 > 0

Hence, the point (-2, -3) lies outside the parabola y\(^{2}\) = 12x.

Therefore, the given statement is not valid.

● The Parabola

• Concept of Parabola
• Standard Equation of a Parabola
• Standard form of Parabola y22 = - 4ax
• Standard form of Parabola x22 = 4ay
• Standard form of Parabola x22 = -4ay
• Parabola whose Vertex at a given Point and Axis is Parallel to x-axis
• Parabola whose Vertex at a given Point and Axis is Parallel to y-axis
• Position of a Point with respect to a Parabola
  
• Parametric Equations of a Parabola
• Parabola Formulae
• Problems on Parabola

11 and 12 Grade Math 

From Position of a Point with respect to a Parabola to HOME PAGE