Mutually Exclusive Events
Definition of Mutually Exclusive Events:
If two events are such that they cannot occur simultaneously for any random experiment are said to be mutually exclusive events.
If X and Y are two mutually exclusive events, then X ∩ Y = ∅
For example, events in rolling of a die are “even face” and “odd face” which are known as mutually exclusive events.
But” odd-face” and “multiple of 3” are not mutually exclusive, because when “face-3” occurs both the events “odd face” and “multiply of 3” are said to be occurred simultaneously.
We see that two simple-events are always mutually exclusive while two compound events may or may not mutually exclusive.
Addition Theorem Based on Mutually Exclusive Events:
If X
and Y are two mutually exclusive
events, then the probability of ‘X union Y’ is the sum of the probability of X and
the probability of Y and represented as,
P(X U Y) = P(X) + P(Y)
Proof: Let E be a random experiment and N(X) be the number of frequency of the event X in E. Since X and Y are two mutually exclusive events then;
N(X U Y) = N(X) + N(Y)
or, N(X U Y)/N = N(X)/N + N(Y)/N; Dividing both the sides by N.
Now taking limit N g ∞, we get probability of
P(X U Y) = P(X) + P(Y)
Worked-out problems on probability of Mutually Exclusive Events:
1. One card is drawn
from a well-shuffled deck of 52 cards. What is the probability of getting a
king or an ace?
Solution:
Let X be the event of ‘getting a king’ and,
Y be the event of ‘getting an ace’
We know that, in a well-shuffled deck of 52 cards there are 4
kings and 4 aces.
Therefore, probability of getting a king from well-shuffled deck of 52 cards = P(X) = 4/52 = 1/13
Similarly, probability of getting an ace from well-shuffled deck of 52 cards = P(Y) = 4/52 = 1/13
According to the definition of mutually exclusive we know that, drawing of a well-shuffled deck of 52 cards ‘getting a king’ and ‘getting an ace’ are known as mutually exclusive events.
We have to find out P(King or ace).
So according to the addition theorem for mutually exclusive events, we get;
P(X U Y) = P(X) + P(Y)
|
Therefore, P(X U Y) |
= 1/13 + 1/13 = (1 + 1)/13 = 2/13 |
Hence, probability of getting a king or an ace from a well-shuffled deck of 52 cards = 2/13
2. A bag contains 8 black pens and 2 red pens and if a pen is drawn at random. What is the probability that it is black pen or red pen?
Solution:
Let X be the event of ‘getting a black pen’ and,
Y be the event of ‘getting a red pen’.
We know that, there are 8 black pens and 2 red pens.
Therefore, probability of getting a black pen = P(X) = 8/10 = 4/5
Similarly, probability of getting a red pen = P(Y) = 2/10 = 1/5
According to the definition of mutually exclusive we know that, the event of ‘getting a black pen’ and ‘getting a red pen’ from a bag are known as mutually exclusive event.
We have to find out P(getting a black pen or getting a red pen).
So according to the
addition theorem for mutually exclusive events, we get;
P(X U Y) = P(X) + P(Y)
|
Therefore, P(X U Y) |
= 4/5 + 1/5 = 5/5 = 1 |
Hence, probability of getting ‘a black pen’ or ‘a red pen’ = 1
Probability
Probability of Tossing Two Coins
Probability of Tossing Three Coins
Probability for Rolling Two Dice
Probability for Rolling Three Dice
From Mutually Exclusive Events to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
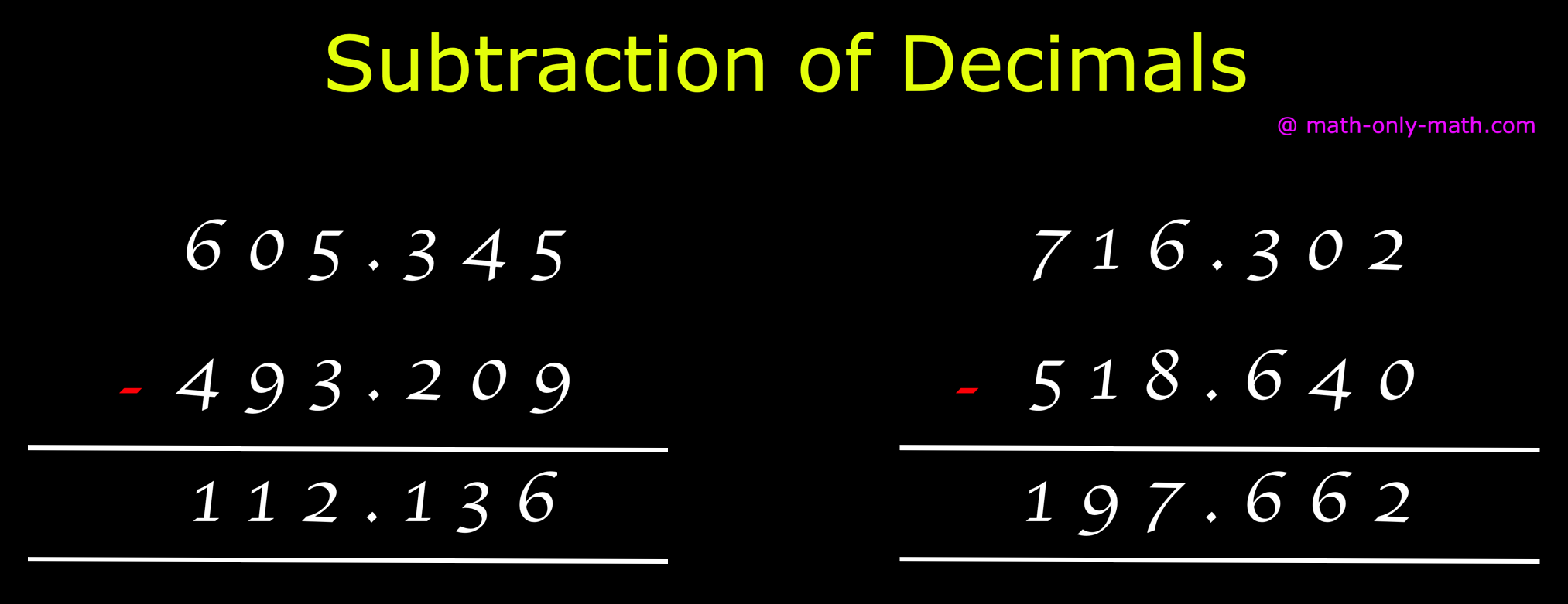
Subtraction of Decimals | Subtracting Decimals | Decimal Subtraction
Apr 24, 25 03:25 PM
We will discuss here about the subtraction of decimals. Decimals are subtracted in the same way as we subtract ordinary numbers. We arrange the digits in columns -
How to Do Long Division? | Method | Steps | Examples | Worksheets |Ans
Apr 24, 25 10:18 AM
As we know that the division is to distribute a given value or quantity into groups having equal values. In long division, values at the individual place (Thousands, Hundreds, Tens, Ones) are dividend… -
Division by Two-Digit Numbers | Knowledge of Estimation | Division
Apr 24, 25 10:12 AM
In division by two-digit numbers we will practice dividing two, three, four and five digits by two-digit numbers. Consider the following examples on division by two-digit numbers: Let us use our knowl… -
Addition of Decimals | How to Add Decimals? | Adding Decimals|Addition
Apr 24, 25 01:45 AM
We will discuss here about the addition of decimals. Decimals are added in the same way as we add ordinary numbers. We arrange the digits in columns and then add as required. Let us consider some -
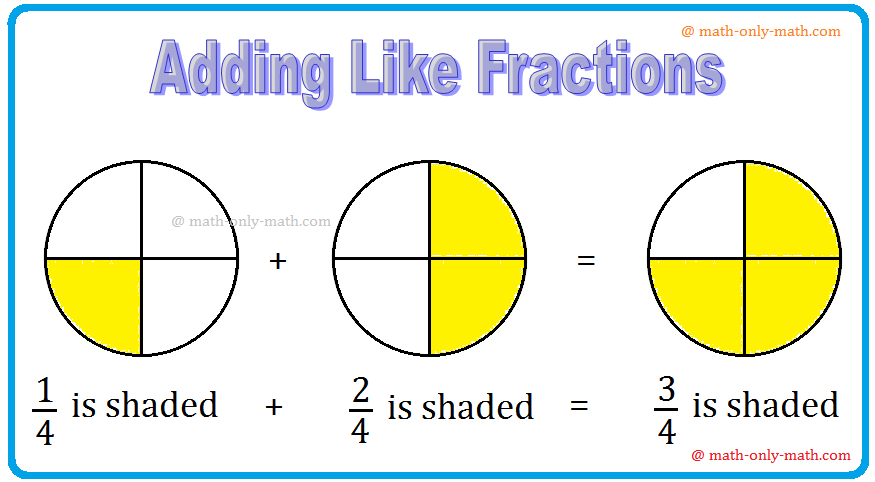
Addition of Like Fractions | Examples | Videos | Worksheet | Fractions
Apr 23, 25 09:23 AM
To add two or more like fractions we simplify add their numerators. The denominator remains same. Thus, to add the fractions with the same denominator, we simply add their numerators and write the com…




New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.