Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Multiplying Fractions
We will discuss here about multiplying fractions by a whole number, by a fractional number or by another mixed fractional number.
I. Multiplication of Fractional Number by a Whole Number:
We have learnt 4 × 5 = 4 times 5
= 5 + 5 + 5 + 5
= 20
In the same way 6 × \(\frac{1}{7}\) = 6 times \(\frac{1}{7}\)
= \(\frac{1}{7}\) + \(\frac{1}{7}\) + \(\frac{1}{7}\) + \(\frac{1}{7}\) + \(\frac{1}{7}\) + \(\frac{1}{7}\)
= \(\frac{1 + 1 + 1 + 1 + 1 + 1}{7}\)
= \(\frac{6}{7}\)
i.e., 6 × \(\frac{1}{7}\) = \(\frac{6 × 1}{7}\) = \(\frac{6}{7}\)
Multiply 4 × \(\frac{3}{5}\)
4 × \(\frac{3}{5}\) = 4 times 4 × \(\frac{3}{5}\)
= \(\frac{3}{5}\) + \(\frac{3}{5}\) + \(\frac{3}{5}\) + \(\frac{3}{5}\)
= \(\frac{12}{5}\)
i.e. 4 × \(\frac{3}{5}\) = \(\frac{4 × 3}{5}\) = \(\frac{12}{5}\)
Product of a whole number and a fractional number =
\(\frac{\textrm{Product of Whole Number × Numerator of the Fractional Number}}{\textrm{Denominator of the Fractional Number}}\)
For examples:
\(\frac{3}{4}\) × 5 = \(\frac{3 × 5}{4}\) = \(\frac{15}{4}\)
\(\frac{6}{7}\) × 2 = \(\frac{6 × 2}{7}\) = \(\frac{12}{7}\)
7 × \(\frac{4}{5}\) = \(\frac{7 × 4}{5}\) = \(\frac{28}{5}\)
4 × \(\frac{3}{11}\) = \(\frac{4 × 3}{11}\) = \(\frac{12}{11}\)
Let us multiply \(\frac{1}{4}\) by 3. We use the rule of repeated addition to find the product.
We can say that \(\frac{1}{4}\) of 3 = \(\frac{3}{4}\)
To multiply a fraction by a whole number, we multiply the
numerator of the fraction by the whole number and reduce the fraction to the
lowest terms, if so required.
For example:
(i) Multiply 1\(\frac{2}{9}\) by 25
Solution:
1\(\frac{2}{9}\) × 25
= \(\frac{1 × 9 + 2}{9}\)
= \(\frac{11}{9}\) × 25
= \(\frac{11 × 25}{9}\)
= \(\frac{275}{9}\)
= 30\(\frac{5}{9}\)
|
(ii) Multiply 2/3 by 7 Solution: 2/3 × 7 = (2 × 7)/3 = 14/3 = 4 2/3 |
We simply multiply the numerator of the fractional number by the whole number. The denominator remains the same. |
|
(iii) Multiply 20 × \(\frac{4}{5}\) 20 × \(\frac{4}{5}\) = \(\frac{20 × 4}{5}\) = \(\frac{2 × 2 × \not 5 × 2 × 2}{\not 5}\) = 16 |
20 = 2 × 2 × 5 4 = 2 × 2 5 = 5 × 1 |
|
(iv) Multiply 2\(\frac{3}{5}\) by 6 Solution: 2\(\frac{3}{5}\) × 6
= (2 × 5 + 3)/5 × 6 = (10 + 3)/5 × 6 = 13/5 × 6 = (13 × 6)/5 = 78/5 = 15\(\frac{3}{5}\) |
We change the mixed numbers into improper fractions and then simply multiply the numerator of the fractional number by the whole number. The denominator remains the same. |
II. Multiplication of Fractional Number by Another Fractional Number:
For example:
|
(i) Multiply 2/5 by 4/5 Solution: 2/5 × 4/5 = (2 × 4)/(5 × 5)
= 8/25 |
Step I: We multiply the numerators. Step II: We multiply the denominators. Step III: We write the fraction in the simplest form. |
|
(ii) Multiply 8/9 by 7/10 Solution: 8/9 × 7/10 = (8 × 7)/(9 × 10)
= 56/90 |
We simply multiply the numerators of the fractional numbers and then multiply the denominators of the fractional numbers. Write the fraction in the simplest form. |
(iii) Multiply \(\frac{4}{7}\) × \(\frac{2}{5}\)
Multiply the numerators to get the numerator of the product and
Multiply the denominators to get the denominator of the product.
Reduce the product to the lowest terms.
Therefore, \(\frac{4}{7}\) × \(\frac{2}{5}\) = \(\frac{4 × 2}{7 × 5}\) = \(\frac{8}{35}\)
III: Product of More than Two Fractions:
For examples:
(i) Multiply \(\frac{9}{10}\) × \(\frac{2}{5}\) × \(\frac{3}{7}\)
Method I: \(\frac{9}{10}\) × \(\frac{2}{5}\) × \(\frac{3}{7}\) = \(\frac{9 × 2 × 3}{10 × 5 × 7}\) = \(\frac{54}{350}\)
H.C.F. of 54 and 350 is 2
\(\frac{54 ÷ 2}{350 ÷ 2}\) = \(\frac{27}{175}\)
Therefore, \(\frac{9}{10}\) × \(\frac{2}{5}\) × \(\frac{3}{7}\) = \(\frac{27}{175}\)
Method II: \(\frac{9}{10}\) × \(\frac{2}{5}\) × \(\frac{3}{7}\) = ?
Write the numbers as the products of prime factors.
Cancel the numbers common in numerator and denominator.
Therefore, \(\frac{9}{10}\) × \(\frac{2}{5}\) × \(\frac{3}{7}\) = \(\frac{3 × 3 × \not 2 × 1 × 3 × 1}{\not 2 × 5 × 5 × 1 × 7 × 1}\)
= \(\frac{27}{175}\)
(v) Multiply \(\frac{4}{7}\), \(\frac{3}{11}\) and \(\frac{5}{8}\).
Solution:
To multiply two or more fractions, we multiply the numerators of given fractions to find the new numerator of the product and multiply the denominators to get the denominator of the product.
Hence, \(\frac{4}{7}\) × \(\frac{3}{11}\) × \(\frac{5}{8}\) = \(\frac{4 × 3 × 5}{7 × 11 × 8}\)
= \(\frac{60}{616}\)
|
(vi) Multiply \(\frac{10}{21}\) × \(\frac{5}{24}\) × \(\frac{3}{50}\) \(\frac{10}{21}\) × \(\frac{5}{24}\) × \(\frac{3}{50}\) = \(\frac{10 × 5 × 3}{21 × 24 × 50}\) = \(\frac{\not 2 × \not 5 × \not 5 × \not 3}{\not 3 × 7 × 3 × \not 2 × 2 × 2 × 2 × \not 5 × \not 5}\) = \(\frac{1}{168}\) |
10 = 2 × 5 5 = 5 × 1 3 = 3 × 1 21 = 3 × 7 24 = 3 × 2 × 2 × 2 50 = 2 × 5 × 5 |
III. Multiplication of a Mixed Number by Another Mixed Number:
For Example:
|
(i) Multiply 2 1/3 by 1 ¾ Solution: 2 1/3 × 1 ¾ = 7/3 × 7/4
= 49/12 = 4 1/12 |
We change the mixed numbers into improper fractions and then we multiply as usual. |
|
(ii) Multiply 1 7/9 by 3 5/11
Solution: 1 7/9 × 3 5/11 = 16/9 × 38/11 = (16 × 38)/(9 × 11) = 608/99 = 6 14/99 |
We change the mixed numbers into improper fractions and then we multiply as usual. |
(iii) Multiply 11\(\frac{7}{8}\) by 3\(\frac{1}{24}\)
Solution:
Let us first convert mixed numbers into improper fractions.
11\(\frac{7}{8}\) = \(\frac{11 × 8 + 7}{8}\) = \(\frac{95}{8}\)
3\(\frac{1}{24}\) = \(\frac{3 × 24 + 1}{24}\) = \(\frac{73}{24}\)
Now, \(\frac{95}{8}\) × \(\frac{73}{24}\) = \(\frac{95 × 73}{8 × 24}\)
= \(\frac{6935}{192}\)
= 36\(\frac{23}{192}\)
(iv) Multiply 3\(\frac{1}{2}\) × 2\(\frac{1}{5}\)
|
3\(\frac{1}{2}\) × 2\(\frac{1}{5}\) = \(\frac{7}{2}\) × \(\frac{11}{5}\) = \(\frac{7 × 11}{2 × 5}\) = \(\frac{77}{10}\) = 7\(\frac{7}{10}\) |
Questions and Answers on Multiplying Fractions:
I. Find the product:
(i) \(\frac{5}{19}\) × 1
(ii) \(\frac{6}{7}\) × 5
(iii) \(\frac{9}{14}\) × 6
(iv) \(\frac{4}{13}\) × 0
(v) \(\frac{1}{7}\) × \(\frac{5}{6}\)
(vi) 1\(\frac{1}{10}\) × 8
(vii) \(\frac{1}{7}\) × \(\frac{8}{1}\)
(viii) \(\frac{1}{3}\) × \(\frac{7}{5}\) × \(\frac{2}{9}\)
(ix) \(\frac{4}{15}\) × \(\frac{10}{21}\)
(x) \(\frac{1}{2}\) of 100
(xi) \(\frac{1}{3}\) of 60
(xii) \(\frac{4}{5}\) of \(\frac{8}{11}\)
Answers:
I. (i) \(\frac{5}{19}\)
(ii) 4\(\frac{2}{7}\)
(iii) 3\(\frac{6}{7}\)
(iv) 0
(v) \(\frac{5}{42}\)
(vi) 8\(\frac{4}{5}\)
(vii) 1\(\frac{1}{7}\)
(viii) \(\frac{14}{135}\)
(ix) \(\frac{8}{63}\)
(x) 50
(xi) 20
(xii) \(\frac{32}{55}\)
II. Multiply and write the product in lowest terms.
(i) \(\frac{1}{2}\) × 40
(ii) \(\frac{1}{3}\) × 150
(iii) \(\frac{2}{7}\) × 21
(iv) \(\frac{7}{38}\) × 0
(v) \(\frac{31}{65}\) × 1
(vi) 8 × \(\frac{17}{24}\)
(vii) \(\frac{3}{7}\) × \(\frac{7}{15}\)
(viii) \(\frac{9}{32}\) × \(\frac{8}{36}\)
(ix) \(\frac{11}{15}\) × \(\frac{45}{88}\)
(x) \(\frac{2}{10}\) ×\(\frac{3}{22}\) ×\(\frac{40}{30}\)
(xi) \(\frac{1}{6}\) ×\(\frac{2}{5}\) ×\(\frac{3}{4}\)
(xii) 3\(\frac{1}{7}\) ×\(\frac{21}{44}\)
Answers:
II. (i) 20
(ii) 50
(iii) 6
(iv) 0
(v) \(\frac{31}{65}\)
(vi) \(\frac{17}{3}\)
(vii) \(\frac{1}{5}\)
(viii) \(\frac{1}{16}\)
(ix) \(\frac{3}{8}\)
(x) \(\frac{2}{55}\)
(xi) \(\frac{1}{20}\)
(xii) 1\(\frac{1}{2}\)
III. Find the Product and Reduce it the Lowest Terms:
(i) 4\(\frac{1}{3}\) × 2\(\frac{1}{3}\)
(ii) 6 × 5\(\frac{1}{2}\)
(iii) 1\(\frac{1}{7}\) × 2\(\frac{1}{4}\)
(iv) \(\frac{3}{4}\) × \(\frac{1}{3}\) × \(\frac{2}{6}\)
(v) 1\(\frac{1}{2}\) × 5\(\frac{2}{3}\) × 4\(\frac{1}{5}\)
(vi) \(\frac{7}{9}\) × \(\frac{10}{15}\) × \(\frac{3}{21}\)
(vii) \(\frac{16}{48}\) × \(\frac{12}{24}\) × \(\frac{15}{30}\)
(viii) \(\frac{19}{38}\) × \(\frac{2}{4}\) × \(\frac{8}{20}\)
(ix) \(\frac{6}{42}\) × 1\(\frac{1}{5}\) × \(\frac{15}{50}\)
Answer:
III. (i) 10\(\frac{1}{9}\)
(ii) 33
(iii) 2\(\frac{4}{7}\)
(iv) \(\frac{1}{12}\)
(v) 35\(\frac{7}{10}\)
(vi) \(\frac{2}{27}\)
(vii) \(\frac{1}{12}\)
(viii) \(\frac{1}{10}\)
(ix) \(\frac{9}{175}\)
IV. Simplify. (use Prime Factorisation)
(i) \(\frac{7}{9}\) × \(\frac{18}{21}\) × \(\frac{6}{10}\)
(ii) \(\frac{24}{36}\) × \(\frac{81}{27}\) × \(\frac{5}{10}\)
(iii) \(\frac{10}{12}\) × \(\frac{12}{14}\) × \(\frac{14}{20}\)
(iv) \(\frac{15}{16}\) × \(\frac{32}{30}\) × \(\frac{1}{4}\)
(v) \(\frac{1}{2}\) × \(\frac{4}{8}\) × \(\frac{16}{6}\)
(vi) \(\frac{13}{22}\) × \(\frac{11}{26}\) × \(\frac{4}{6}\)
Answer:
IV. (i) \(\frac{2}{5}\)
(ii) 1
(iii) \(\frac{1}{2}\)
(iv) \(\frac{1}{4}\)
(v) \(\frac{2}{3}\)
(vi) \(\frac{1}{6}\)
V. Multiply:
(i) 4 × \(\frac{6}{11}\)
(ii) \(\frac{8}{13}\) × 3
(iii) \(\frac{2}{5}\) × 10
(iv) \(\frac{5}{7}\) × 5
(v) 8 × \(\frac{5}{6}\)
(vi) \(\frac{7}{12}\) × 2
(vii) 15 × \(\frac{1}{4}\)
(viii) 19 × \(\frac{1}{3}\)
Answer:
V. (i) 2\(\frac{2}{11}\)
(ii) 1\(\frac{11}{13}\)
(iii) 4
(iv) 3\(\frac{4}{7}\)
(v) 6\(\frac{2}{3}\)
(vi) 1\(\frac{1}{6}\)
(vii) 3\(\frac{3}{4}\)
(viii) 6\(\frac{1}{3}\)
VI. Find the given quantity.
(i) \(\frac{1}{7}\) of 28 kg apples
(ii) \(\frac{2}{15}\) of $300
(iii) \(\frac{5}{9}\) of 54 km
(iv) \(\frac{2}{5}\) of 70 chairs
Answers:
VI. (i) 4 kg apples
(ii) $40
(iii) 30 km
(iv) 28 chairs
VII: Word problems on Multiplying Fractions:
1. 2\(\frac{1}{5}\) m of cloth is required to make a shirt. Ron wants to make 25 shirts, what length of cloth does he need?
Answer: 55 m of cloth
2. \(\frac{3}{4}\) cups of milk is required to make a cake of 1 kg. How many cups of milk is required to make a cake of 4\(\frac{1}{2}\) kg?
Answer: 3\(\frac{3}{8}\) cups
3. Shelly bought 16\(\frac{3}{4}\) liters of juice. If the cost of 1 liter juice is $8, find the total cost of juice?
Answer: $134
4. The weight of each bag is 4\(\frac{1}{4}\) Kg. What would be the weight of 36 such bags?
Answer: 153 kg
5. Sam works for 6\(\frac{2}{8}\) hours each day. For how much time will she work in a month if she works for 24 days in a month?
Answer: 150 hours
● Related Concepts
- Fraction of a Whole Numbers
- Representation of a Fraction
- Equivalent Fractions
- Properties of Equivalent Fractions
- Finding Equivalent Fractions
- Reducing the Equivalent Fractions
- Verification of Equivalent Fractions
- Finding a Fraction of a Whole Number
- Like and Unlike Fractions
- Comparison of Like Fractions
- Comparison of Fractions having the same Numerator
- Comparison of Unlike Fractions
- Fractions in Ascending Order
- Fractions in Descending Order
- Types of Fractions
- Changing Fractions
- Conversion of Fractions into Fractions having Same Denominator
- Conversion of a Fraction into its Smallest and Simplest Form
- Addition of Fractions having the Same Denominator
- Addition of Unlike Fractions
- Addition of Mixed Fractions
- Word Problems on Addition of Mixed Fractions
- Worksheet on Word Problems on Addition of Mixed Fractions
- Subtraction of Fractions having the Same Denominator
- Subtraction of Unlike Fractions
- Subtraction of Mixed Fractions
- Word Problems on Subtraction of Mixed Fractions
- Worksheet on Word Problems on subtraction of Mixed Fractions
- Addition and Subtraction of Fractions on the Fraction Number Line
- Word Problems on Multiplication of Mixed Fractions
- Worksheet on Word Problems on Multiplication of Mixed Fractions
- Multiplying Fractions
- Dividing Fractions
- Word Problems on Division of Mixed Fractions
- Worksheet on Word Problems on Division of Mixed Fractions
From Multiplying Fractions to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.

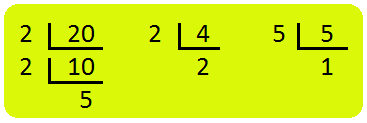


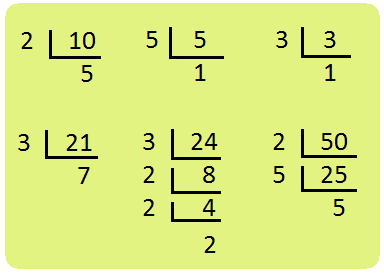
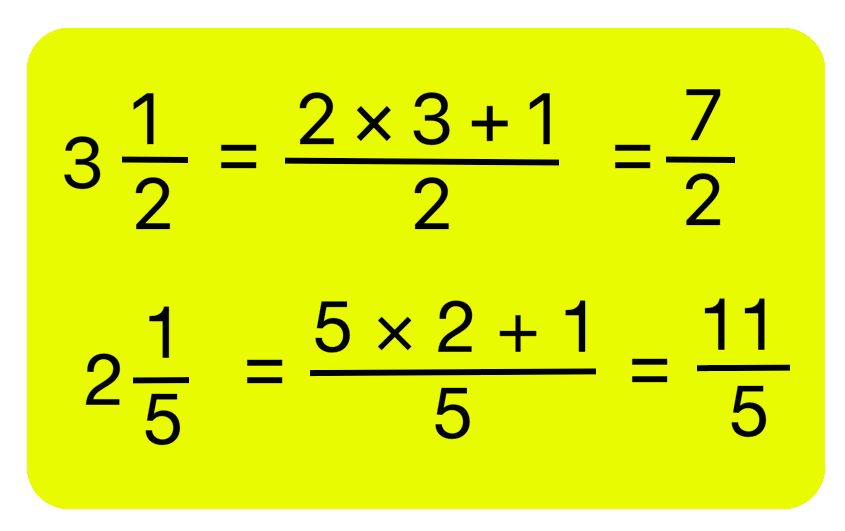



New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.