Median of Raw Data
The median of raw data is the number which divides the observations when arranged in an order (ascending or descending) in two equal parts.
Method of finding median
Take the following steps to find the median of raw data.
Step I: Arrange the raw data in ascending or descending order.
Step II: Observe the number of variates in the data. Let the number of variates in the data be n. Then find the median as following.
(i) If n is odd then n+12th variate is the median.
(ii) If n is even then the mean of n2th and (n2 + 1)th variates is the median, i.e.,
median = 12{n2th Variate+(n2+1)th Variate}.
Solved Examples on Median of Raw Data or Median of Ungrouped Data:
1. Find the median of the ungrouped data.
15, 18, 10, 6, 14
Solution:
Arranging variates in ascending order, we get
6, 10, 14, 15, 18.
The number of variates = 5, which is odd.
Therefore, median = 5+12th variate
= 3rd variate
= 14.
2. Find the median of the raw data.
8, 7, 15, 12, 10, 8, 9
Solution:
Arranging the variates in ascending order, we get
7, 8, 8, 9, 10, 12, 15.
The number of variates = 7, which is odd.
Therefore, median = the 7+12th variate
= 4th variate
= 9.
3. Find the median of the ungrouped data.
10, 17, 16, 21, 13, 18, 12, 10.
Solution:
Arranging the variates in ascending order, we get
10, 17, 16, 21, 13, 18, 12, 10.
The number of variates = 8, which is even.
Therefore, median = mean of the 82th and (82 + 1)th variate
= mean of the 4th and 5th variates
= mean of 13 and 16
= (13+162
= (292
= 14.5.
4. Find the median of the raw data.
8, 7, 5, 6, 3, 8, 5, 3
Solution:
Arranging variates in descending order, we get
8, 8, 7, 6, 5, 5, 3, 3.
The number of variates = 8, which is even.
Therefore, median = mean of 82th and (82 + 1)th variate
= mean of 4th and 5th variate
= mean of 6 and 5
= 6+52
= 5.5
Note: The median need not be form among the variates.
From Median of Raw Data to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Converting Fractions to Decimals | Solved Examples | Free Worksheet
Apr 26, 25 05:04 PM
In converting fractions to decimals, we know that decimals are fractions with denominators 10, 100, 1000 etc. In order to convert other fractions into decimals, we follow the following steps: -
Converting Decimals to Fractions | Solved Examples | Free Worksheet
Apr 26, 25 04:56 PM
In converting decimals to fractions, we know that a decimal can always be converted into a fraction by using the following steps: Step I: Obtain the decimal. Step II: Remove the decimal points from th… -
Worksheet on Decimal Numbers | Decimals Number Concepts | Answers
Apr 26, 25 03:48 PM
Practice different types of math questions given in the worksheet on decimal numbers, these math problems will help the students to review decimals number concepts. -
Multiplication Table of 4 |Read and Write the Table of 4|4 Times Table
Apr 26, 25 01:00 PM
Repeated addition by 4’s means the multiplication table of 4. (i) When 5 candle-stands having four candles each. By repeated addition we can show 4 + 4 + 4 + 4 + 4 = 20 Then, four 5 times -
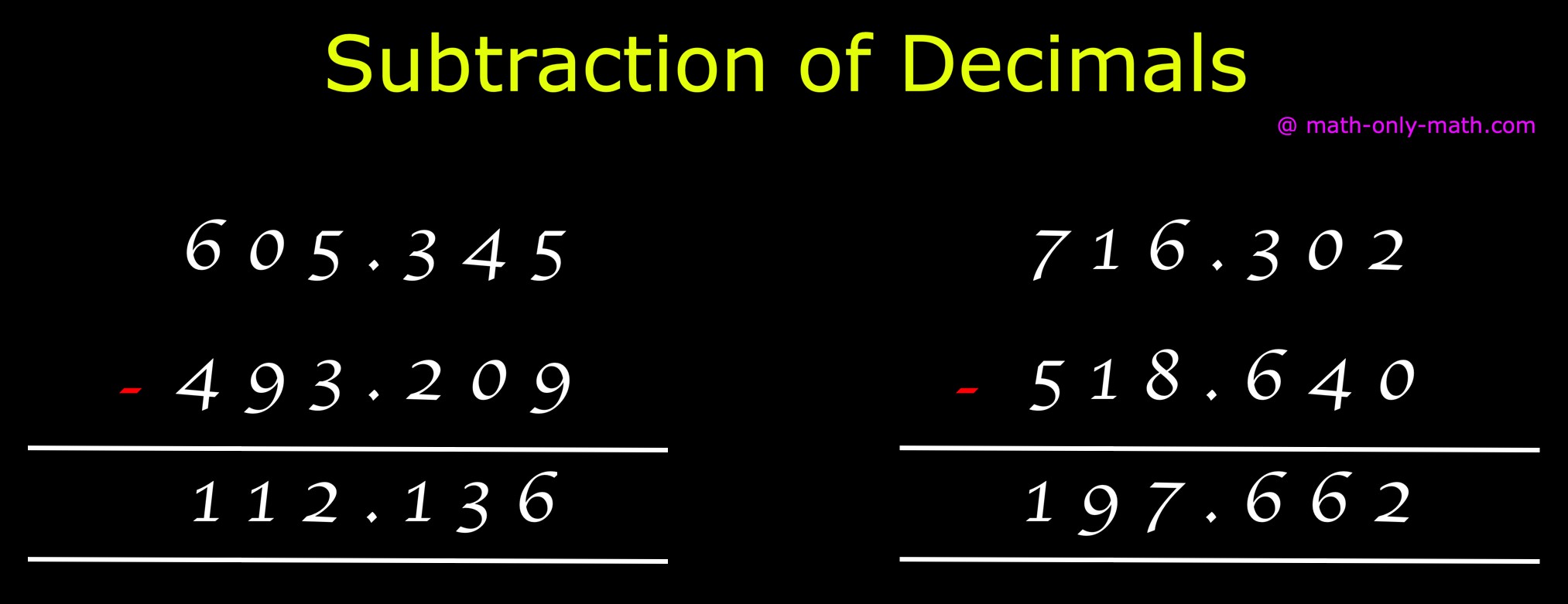
Subtraction of Decimals | Subtracting Decimals | Decimal Subtraction
Apr 24, 25 03:25 PM
We will discuss here about the subtraction of decimals. Decimals are subtracted in the same way as we subtract ordinary numbers. We arrange the digits in columns




New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.