Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Long Division Method with Regrouping and without Remainder
We will discuss here how to solve step-by-step the long division method with regrouping and without remainder.
Consider the following examples:
A. Dividing a 2-Digits Number by 1-Digit Number With Regrouping and Without Remainder:
Division by Regrouping 2-digit Numbers
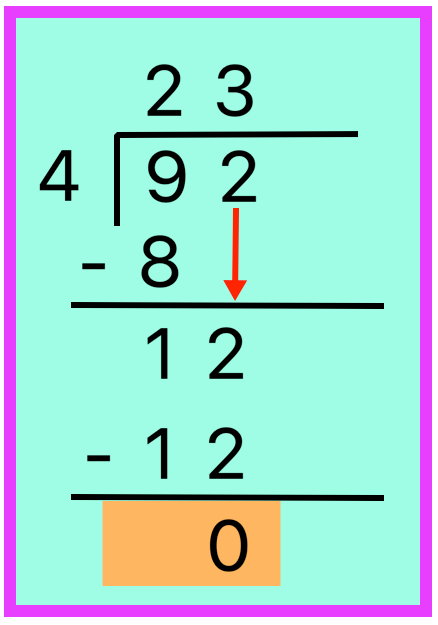
1. Divide 92 by 4.
Solution:
Step I: Arrange the numbers in columns.
Divide 9 tens by 4.
4 × 2 = 8, 8 < 9
and 4 × 3 = 12, 12 > 9
So, 9 - 8 = 1
We have 1 ten left.
Step II:
Bring down 2 ones.
We now have 1 ten and 2 ones = 12 ones as the new dividend.
On reciting the table of 4,
we get 4 × 3 = 12
So, the quotient is 23.
B. Dividing a 3-Digits Number by 1-Digit Number With Regrouping and Without Remainder:
Division by Regrouping 3-digit Numbers
1. 468 ÷ 3
Let us follow the division along with the given steps.
 |
Step I: Begin with hundreds digit 4 hundreds ÷ 3 = 1 hundred with remainder 1 hundred
Step II: Bring down 6 tens to the right of 1 hundred 1 hundred + 6 tens = 16 tens Step III: 16 tens ÷ 3 = 5 tens with remainder 1 ten Step IV: Bring down 8 ones to the right of 1 ten 1 ten + 8 ones = 18 ones Step V: 18 ones ÷ 3 = 6 ones |
Therefore, 468 ÷ 3 = 156
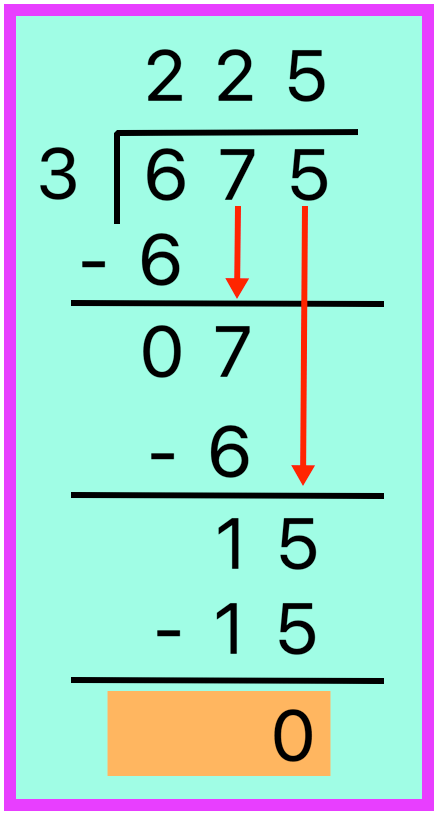
2. Divide 675 by 3.
Solution:
Step I: Divide the 6 hundreds. (3 × 2 = 6)
Subtract the hundreds: 6 - 6 = 0
Step II: Divide the 7 tens. (3 × 2 = 6)
Subtract the tens: 7 - 6 = 1,
i.e., 1 ten is left.
So, bring down 5 ones.
Step III: Now, we have 10 ones (1 ten) + 5 ones = 15 ones.
Divide 15 ones by 3. (3 × 5 = 15)
Subtract the ones:
15 - 15 = 0
Therefore, Quotient = 225, Remainder = 0.
C. Dividing a 4-Digits Number by 1-Digit Number With Regrouping and Without Remainder:
1. 9120 ÷ 5
Let us follow the division along with the given steps.
 |
Step I: Begin with thousands digit 9 thousands ÷ 5 = 1 thousand with remainder 4 thousands
Step II: Bring down 1 hundred to the right of 4 thousands Step III: Now 4 thousands + 1 hundred = 41 hundreds Step IV: Now 41 hundreds ÷ 5 = 8 hundreds with remainder 1 hundred Step V: Bring down 2 tens to the right of 1 hundred Step VI: Now 1 hundred + 2 tens = 12 tens Step VII: So, 12 tens ÷ 5 = 2 with remainder 2 tens Step VIII: Bring down zero to the right of 2 tens So, 2 tens + 0 ones = 20 ones Now 20 ones ÷ 5 = 4 ones |
Therefore, 9120 ÷ 5 = 1824
From Long Division Method with Regrouping and without Remainder to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
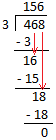
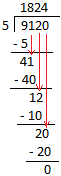
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.