Important Properties of Transverse Common Tangents

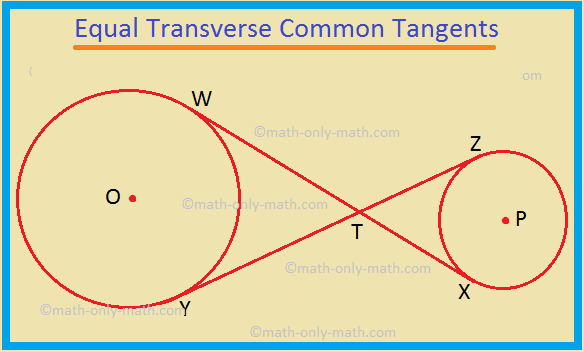
I. The two transverse common tangents drawn to two circles are equal in length.

Given:

WX and YZ are two transverse common tangents drawn to the two given circles with centres O and P. WX and YZ intersect at T.

To prove: WX = YZ.

Proof:

II. The length of a transverse common tangent to two circles is $\sqrt{d^{2} – (r_{1} + r_{2})^{2}}$, where d is the distance between the centres of the circles, and r$_{1}$ and r$_{2}$ are the radii of the given circles.

Proof:

Let two circles be given with centres O and P, and radii r$_{1}$ and r$_{2}$ respectively, where r$_{1}$ < r$_{2}$. Let the distance between the centres of the circles, OP = d.

Let WX be a transverse common tangent.

Therefore, OW = r$_{1}$ and PX = r$_{2}$.

Also, OW ⊥ WX and PX ⊥ WX, because a tangent is perpendicular to the radius drawn through the point of contact

Produce W to T such that WT = PX = r$_{2}$. Join T to P. In the quadrilateral WXPT, WT ∥ PX, as both are perpendiculars to WX; and WT = PX. Therefore, WXPT is a rectangle. Thus, WX = PT, as the opposite sides of a rectangle are equal.

OT = OW + WT = r$_{1}$  +  r$_{2}$.

In the right-angled triangle OPT, we have

PT² = OP² – OT² (by Pythagoras’ Theorem)

⟹ PT² = d² – (r$_{1}$ + r$_{1}$)$^{2}$

⟹ PT = $\sqrt{d^{2} – (r_{1} + r_{2})^{2}}$

⟹ WX = $\sqrt{d^{2} – (r_{1} + r_{2})^{2}}$ (Since, PT = WX).

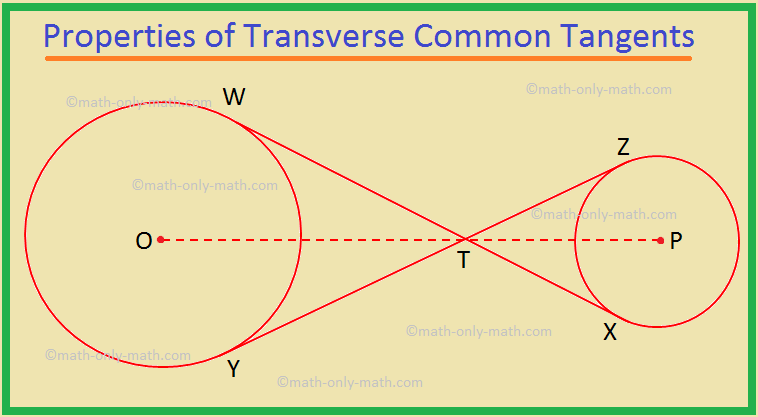
III. The transverse common tangents drawn to two circles intersect on the line drawn through the centres of the circles.

Given: Two circles with centres O and P, and their transverse common tangents WX and YZ, which intersects at T

To prove: T lies on the line joining O to P, i.e., O T and P lie on the same straight line.

Proof:

10th Grade Math

From Important Properties of Transverse Common Tangents to HOME PAGE