Functions or Mapping
Now, in functions or mapping we will study about special type of relations called functions or mapping. To understand them, let us take few real life examples.
| All these questions have unique answers. Let us see how we can relate this in learning mapping. |
● From where does the sun rise?
East
● Which is the capital of India?
Delhi
● What is the successor of 4?
5
● What is the sum o f 5 and 3?
8
Mapping or Functions:
If A and B are two non-empty sets, then a relation ‘f‘ from set A to set B is said to be a function or mapping,
● If every element of set A is associated with unique element of set B.
● The function ‘f’ from A to B is denoted by f : A → B.
● If f is a function from A to B and x ∈ A, then f(x) ∈ B where f(x) is called the image of x under f and x is called the pre image of f(x) under ‘f’.
Note:
For f to be a mapping from A to B:
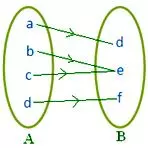
● Every element of A must have image in B. Adjoining figure does not represent a mapping since the element d in set A is not associated with any element of set B.
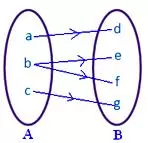
● No element of A must have more than one image. Adjoining figure does not represent a mapping since element b in set A is associated with two elements d, f of set B.
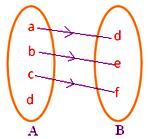
● Different elements of A can have the same image in B. Adjoining figure represents a mapping.
Note:
Every mapping is a relation but every relation may not be a mapping.
Function as a special kind of relation:
Let us recall and review the function as a special kind of relation suppose, A and B are two non-empty sets, then a rule 'f' that associates each element of A with a unique element of B is called a function or a mapping from A to B.
If 'f' is a mapping from A to B,
we express it as f: A → B
we read it as 'f' is a function from A to B.
If ‘f ' is a function from A to B and x∈A and y∈B, then we say that y is the image of element x under the function ' f ' and denoted it by f(x).
Therefore, we write it as y = f(x)
Here, element x is called the pre-image of y.
Thus, for a function from A to B.
● A and B should be non-empty.
● Each element of A should have image in B.
● No element of 'A' should have more than one image in 'B’.
Note:
● Two or more elements of A may have the same image in B.
● f : x → y means that under the function of 'f' from A to B, an element x of A has image y in B.
● It is necessary that every f image is in B but there may be some elements in B which are not f images of any element of A.
● Relations and Mapping
Domain and Range of a Relation
Domain Co-domain and Range of Function
● Relations and Mapping - Worksheets
Worksheet on Functions or Mapping
8th Grade Math Practice
From Functions or Mapping to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
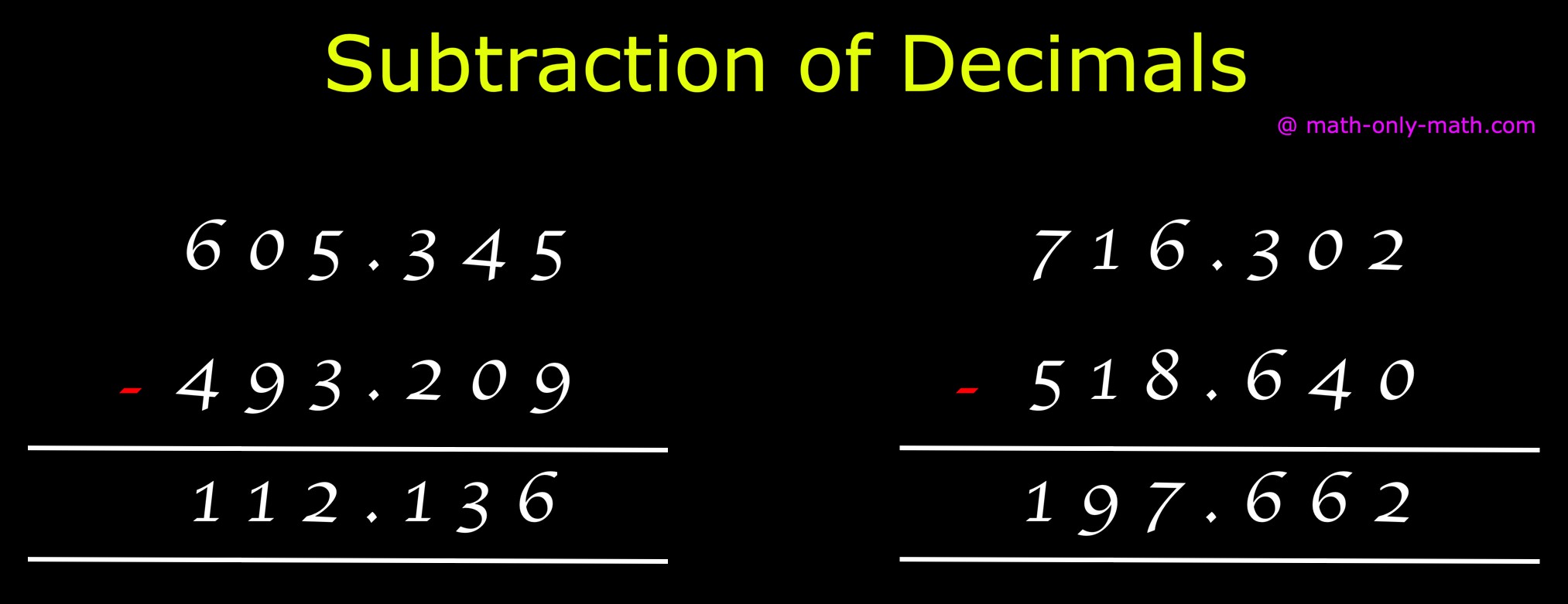
Subtraction of Decimals | Subtracting Decimals | Decimal Subtraction
Apr 24, 25 03:25 PM
We will discuss here about the subtraction of decimals. Decimals are subtracted in the same way as we subtract ordinary numbers. We arrange the digits in columns -
How to Do Long Division? | Method | Steps | Examples | Worksheets |Ans
Apr 24, 25 10:18 AM
As we know that the division is to distribute a given value or quantity into groups having equal values. In long division, values at the individual place (Thousands, Hundreds, Tens, Ones) are dividend… -
Division by Two-Digit Numbers | Knowledge of Estimation | Division
Apr 24, 25 10:12 AM
In division by two-digit numbers we will practice dividing two, three, four and five digits by two-digit numbers. Consider the following examples on division by two-digit numbers: Let us use our knowl… -
Addition of Decimals | How to Add Decimals? | Adding Decimals|Addition
Apr 24, 25 01:45 AM
We will discuss here about the addition of decimals. Decimals are added in the same way as we add ordinary numbers. We arrange the digits in columns and then add as required. Let us consider some -
Addition of Like Fractions | Examples | Videos | Worksheet | Fractions
Apr 23, 25 09:23 AM
To add two or more like fractions we simplify add their numerators. The denominator remains same. Thus, to add the fractions with the same denominator, we simply add their numerators and write the com…




New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.