Equation of a Circle when the Line Segment Joining Two Given Points is a Diameter

We will learn how to find the equation of the circle for which the line segment joining two given points is a diameter.

the equation of the circle drawn on the straight line joining two given points (x\(_{1}\), y\(_{1}\)) and (x\(_{2}\), y\(_{2}\)) as diameter is (x - x\(_{1}\))(x - x\(_{2}\))  + (y - y\(_{1}\))(y - y\(_{2}\)) = 0

First Method:

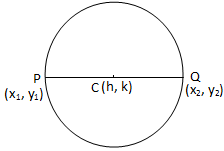
Let P (x\(_{1}\), y\(_{1}\)) and Q (x\(_{2}\), y\(_{2}\)) are the two given given points on the circle. We have to find the equation of the circle for which the line segment PQ is a diameter.

Therefore, the mid-point of the line segment PQ is (\(\frac{x_{1} + x_{2}}{2}\), \(\frac{y_{1} + y_{2}}{2}\)).

Now see that the mid-point of the line segment PQ is the centre of the required circle.

The radius of the required circle

= \(\frac{1}{2}\)PQ

= \(\frac{1}{2}\)\(\mathrm{\sqrt{(x_{1} - x_{2})^{2} + (y_{1} - y_{2})^{2}}}\)

We know that the equation of a circle with centre at (h, k) and radius equal to a, is (x - h)\(^{2}\) + (y - k)\(^{2}\) = a\(^{2}\).

Therefore, the equation of the required circle is

(x - \(\frac{x_{1} + x_{2}}{2}\))\(^{2}\) + (y - \(\frac{y_{1} + y_{2}}{2}\))\(^{2}\) = [\(\frac{1}{2}\)\(\mathrm{\sqrt{(x_{1} - x_{2})^{2} + (y_{1} - y_{2})^{2}}}\) ]\(^{2}\)

⇒ (2x - x\(_{1}\) - x\(_{2}\))\(^{2}\) + (2y - y\(_{1}\) - y\(_{2}\))\(^{2}\) = (x\(_{1}\) - x\(_{2}\))\(^{2}\) + (y\(_{1}\) - y\(_{2}\))\(^{2}\)

⇒ (2x - x\(_{1}\) - x\(_{2}\))\(^{2}\) - (x\(_{1}\) - x\(_{2}\))\(^{2}\) + ( 2y - y\(_{1}\) - y\(_{2}\) )\(^{2}\) - (y\(_{1}\) - y\(_{2}\))\(^{2}\) = 0

⇒ (2x - x\(_{1}\) - x\(_{2}\) + x\(_{1}\) - x\(_{2}\))(2x - x\(_{1}\) - x\(_{2}\) - x\(_{1}\) + x\(_{2}\)) + (2y - y\(_{1}\) - y\(_{2}\) + y\(_{1}\) - y\(_{2}\))(2y - y\(_{1}\) - y\(_{2}\) + y\(_{2}\)) = 0

⇒ (2x - 2x\(_{2}\))(2x - 2x\(_{1}\)) + (2y - 2y\(_{2}\))(2y - 2y\(_{1}\)) = 0

⇒ (x - x\(_{2}\))(x - x\(_{1}\)) + (y - y\(_{2}\))(y - y\(_{1}\)) = 0

⇒ (x - x\(_{1}\))(x - x\(_{2}\)) + (y - y\(_{1}\))(y - y\(_{2}\)) = 0.

 

Second Method:

equation of a circle when the co-ordinates of end points of a diameter are given

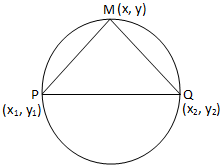
Let the two given points be P (x\(_{1}\), y\(_{1}\)) and Q (x\(_{2}\), y\(_{2}\)). We have to find the equation of the circle for which the line segment PQ is a diameter.

Let M (x, y) be any point on the required circle. Join PM and MQ.

m\(_{1}\) = the slope of the straight line PM = \(\frac{y - y_{1}}{x - x_{1}}\)

m\(_{2}\) = the slope of the straight line PQ = \(\frac{y - y_{2}}{x - x_{2}}\).

Now, since the angle subtended at the point M in the semi-circle PMQ is a right angle.

Now, PQ is a diameter of the required circle.

Therefore, ∠PMQ = 1 rt. angle i.e., PM is perpendicular to QM

Therefore, \(\frac{y - y_{1}}{x - x_{1}}\) × \(\frac{y - y_{2}}{x - x_{2}}\) = -1

⇒ (y - y\(_{1}\))(y - y\(_{2}\)) = - (x - x\(_{1}\))(x - x\(_{2}\)) 

⇒ (x - x\(_{1}\))(x - x\(_{2}\)) + (y - y\(_{1}\))(y - y\(_{2}\)) = 0.

This is the required equation of the circle having (x\(_{1}\), y\(_{1}\)) and (x\(_{2}\), y\(_{2}\)) as the coordinates of the end points of a diameter.

Note: If the coordinates of the end points of a diameter of a circle given, we can also find the equation of the circle by finding the coordinates of the centre and radius. The centre is the mid-point of the diameter and radius is half of the length of the diameter.

● The Circle

• Definition of Circle
• Equation of a Circle
• General Form of the Equation of a Circle
• General Equation of Second Degree Represents a Circle
• Centre of the Circle Coincides with the Origin
• Circle Passes through the Origin
• Circle Touches x-axis
• Circle Touches y-axis
• Circle Touches both x-axis and y-axis
• Centre of the Circle on x-axis
• Centre of the Circle on y-axis
• Circle Passes through the Origin and Centre Lies on x-axis
• Circle Passes through the Origin and Centre Lies on y-axis
• Equation of a Circle when Line Segment Joining Two Given Points is a Diameter
• Equations of Concentric Circles
  
• Circle Passing Through Three Given Points
• Circle Through the Intersection of Two Circles
• Equation of the Common Chord of Two Circles
• Position of a Point with Respect to a Circle
• Intercepts on the Axes made by a Circle
• Circle Formulae
• Problems on Circle 

11 and 12 Grade Math 

From Equation of a Circle when the Line Segment Joining Two Given Points is a Diameter to HOME PAGE