Domain and Range of a Relation

In domain and range of a relation, if R be a relation from set A to set B, then

• The set of all first components of the ordered pairs belonging to R is called the domain of R.
Thus, Dom(R) = {a ∈ A: (a, b) ∈ R for some b ∈ B}.

• The set of all second components of the ordered pairs belonging to R is called the range of R.

Thus, range of R = {b ∈ B: (a, b) ∈R for some a ∈ A}.

Therefore, Domain (R) = {a : (a, b) ∈ R} and Range (R) = {b : (a, b) ∈ R}

Note:

The domain of a relation from A to B is a subset of A. 

The range of a relation from A to B is a subset of B.

For Example:

If A = {2, 4, 6, 8)   B = {5, 7, 1, 9}.

Let R be the relation ‘is less than’ from A to B. Find Domain (R) and Range (R).

Solution:

Under this relation (R), we have

R = {(4, 5); (4, 7); (4, 9); (6, 7); (6, 9), (8, 9) (2, 5) (2, 7) (2, 9)}

Therefore, Domain (R) = {2, 4, 6, 8} and Range (R) = {1, 5, 7, 9}

Solved examples on domain and range of a relation:

1. In the given ordered pair (4, 6); (8, 4); (4, 4); (9, 11); (6, 3); (3, 0); (2, 3) find the following relations. Also, find the domain and range.

(a) Is two less than

(b) Is less than

(c) Is greater than

(d) Is equal to

Solution:

(a) R₁ is the set of all ordered pairs whose 1ˢᵗ component is two less than the 2ⁿᵈ component.

Therefore, R₁ = {(4, 6); (9, 11)}

Also, Domain (R₁) = Set of all first components of R₁ = {4, 9} and Range (R₂) = Set of all second components of R₂ = {6, 11}

(b) R₂ is the set of all ordered pairs whose 1ˢᵗ component is less than the second component.

Therefore, R₂ = {(4, 6); (9, 11); (2, 3)}.

Also, Domain (R₂) = {4, 9, 2} and Range (R₂) = {6, 11, 3}

(c) R₃ is the set of all ordered pairs whose 1ˢᵗ component is greater than the second component.

Therefore, R₃ = {(8, 4); (6, 3); (3, 0)}

Also, Domain (R₃) = {8, 6, 3} and Range (R₃) = {4, 3, 0}

(d) R₄ is the set of all ordered pairs whose 1ˢᵗ component is equal to the second component.

Therefore, R₄ = {(3, 3)}

Also, Domain (R) = {3} and Range (R) = {3}

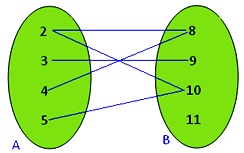
2. Let A = {2, 3, 4, 5} and B = {8, 9, 10, 11}.

Let R be the relation ‘is factor of’ from A to B.

(a) Write R in the roster form. Also, find Domain and Range of R.

(b) Draw an arrow diagram to represent the relation.

Solution:

(a) Clearly, R consists of elements (a, b) where a is a factor of b.

Therefore, Relation (R) in the roster form is R = {(2, 8); (2, 10); (3, 9); (4, 8), (5, 10)}

Therefore, Domain (R) = Set of all first components of R = {2, 3, 4, 5} and Range (R) = Set of all second components of R = {8, 10, 9}

(b) The arrow diagram representing R is as follows:

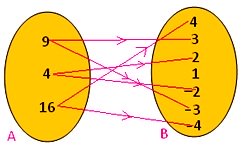
3. The arrow diagram shows the relation (R) from set A to set B. Write this relation in the roster form.

Solution:

Clearly, R consists of elements (a, b), such that ‘a’ is square of ‘b’
i.e., a = b².

So, in roster form R = {(9, 3); (9, -3); (4, 2); (4, -2); (16, 4); (16, -4)}

Worked-out problems on domain and range of a relation:

4. Let A = {1, 2, 3, 4, 5} and B = {p, q, r, s}. Let R be a relation from A in B defined by
R = {1, p}, (1, r), (3, p), (4, q), (5, s), (3, p)}

Find domain and range of R.

Solution:

Given R = {(1, p), (1, r), (4, q), (5, s)}

Domain of R = set of first components of all elements of R = {1, 3, 4, 5}

Range of R = set of second components of all elements of R = {p, r, q, s}

5. Determine the domain and range of the relation R defined by

R = {x + 2, x + 3} : x ∈ {0, 1, 2, 3, 4, 5}

Solution:

Since, x = {0, 1, 2, 3, 4, 5}

Therefore,

      x = 0 ⇒ x + 2 = 0 + 2 = 2 and x + 3 = 0 + 3 = 3

      x = 1 ⇒ x + 2 = 1 + 2 = 3 and x + 3 = 1 + 3 = 4

      x = 2 ⇒ x + 2 = 2 + 2 = 4 and x + 3 = 2 + 3 = 5

      x = 3 ⇒ x + 2 = 3 + 2 = 5 and x + 3 = 3 + 3 = 6

      x = 4 ⇒ x + 2 = 4 + 2 = 6 and x + 3 = 4 + 3 = 7

      x = 5 ⇒ x + 2 = 5 + 2 = 7 and x + 3 = 5 + 3 = 8

Hence, R = {(2, 3), (3, 4), (4, 5), (5, 6), (6, 7), (7, 8)}

Therefore, Domain of R = {a : (a, b) ∈R} = Set of first components of all ordered pair belonging to R.

Therefore, Domain of R = {2, 3, 4, 5, 6, 7}

Range of R = {b : (a, b) ∈ R} = Set of second components of all ordered pairs belonging to R.

Therefore, Range of R = {3, 4, 5, 6, 7, 8}

6. Let A = {3, 4, 5, 6, 7, 8}. Define a relation R from A to A by

    R = {(x, y) : y = x - 1}.

• Depict this relation using an arrow diagram.

• Write down the domain and range of R.

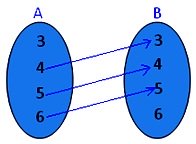
Solution:

By definition of relation

R = {(4, 3) (5, 4) (6, 5)}

The corresponding arrow diagram is shown.

We can see that domain = {4, 5, 6} and Range = {3, 4, 5}

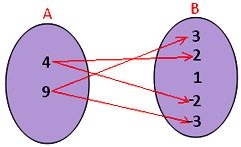
7. The adjoining figure shows a relation between the sets A and B.

Write this relation in

  • Set builder form

  • Roster form

  • Find the domain and range

Solution:

We observe that the relation R is 'a’ is the square of ‘b'.

In set builder form R = {(a, b) : a is the square of b, a ∈ A, b ∈ B}

In roster form R = {(4, 2) (4, -2)(9, 3) (9, -3)}

Therefore, Domain of R = {4, 9}

Range of R = {2, -2, 3, -3}

Note: The element 1 is not related to any element in set A.

● Relations and Mapping

Ordered Pair

Cartesian Product of Two Sets

Relation

Domain and Range of a Relation

Functions or Mapping

Domain Co-domain and Range of Function

● Relations and Mapping - Worksheets

Worksheet on Math Relation

Worksheet on Functions or Mapping

7th Grade Math Problems 

8th Grade Math Practice 

From Domain and Range of a Relation to HOME PAGE