Conversion of Fractions
Conversion of fractions is discussed here in order to convert a mixed fraction into an improper fraction and also to convert an improper fraction as a mixed fraction.
Method of reduction of different fractions into like fractions:
Step I: Find the L.C.M of all the denominators.
Step II: Divide the L.C.M by the denominator of the first fraction and get the quotient.
Step III: Multiply both numerator and denominator of the first fraction by the quotient.
Step IV: Repeat step 2 and 3 for all the given fractions.
In order to convert a mixed fraction into an improper fraction, we may use the following formula;
Improper fraction = {(Whole number x Denominator) + Numerator} Denominator
For example;
(i) 31/5 = (3 × 5 + 1)/5 = (15 + 1)/5 = 16/5
(ii) 93/4 = (9 × 4 + 3)/4 = (36 + 3)/4 = 39/4
In order to convert an improper fraction as a mixed fraction, we first divide the numerator by denominator and obtain the quotient and remainder and then we write the mixed fraction as
Quotient = Remainder
Denominator
For example;
(i) ¹⁷/₄ = 4¹/₄ [Since, Quotient = 4, Remainder = 1]
(ii) ⁴⁷/₁₅ = 3²/₁₅ [Since, Quotient = 3, Remainder = 2]
Note:
If the numerator and denominator of a fraction are both multiplied by the same non-zero number, then its value does not change.
= (4 × 6)/(5 × 6) etc.
If the numerator and denominator of a fraction are both divided by their common factor, then its value does not change.
i.e., 6/10 = (6 ÷ 2)/(10 ÷ 2) = 3/5;
9/24 = (9 ÷ 3)/(24 ÷ 3) = 3/8 etc.
These are the basic examples on conversion of fractions explained here step by step.
● Fractions
Addition and Subtraction of Fractions
● Fractions - Worksheets
Worksheet on Multiplication of Fractions
Worksheet on Division of Fractions
7th Grade Math Problems
From Conversion of Fractions to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Addition of Decimals | How to Add Decimals? | Adding Decimals|Addition
Apr 24, 25 01:45 AM
We will discuss here about the addition of decimals. Decimals are added in the same way as we add ordinary numbers. We arrange the digits in columns and then add as required. Let us consider some -
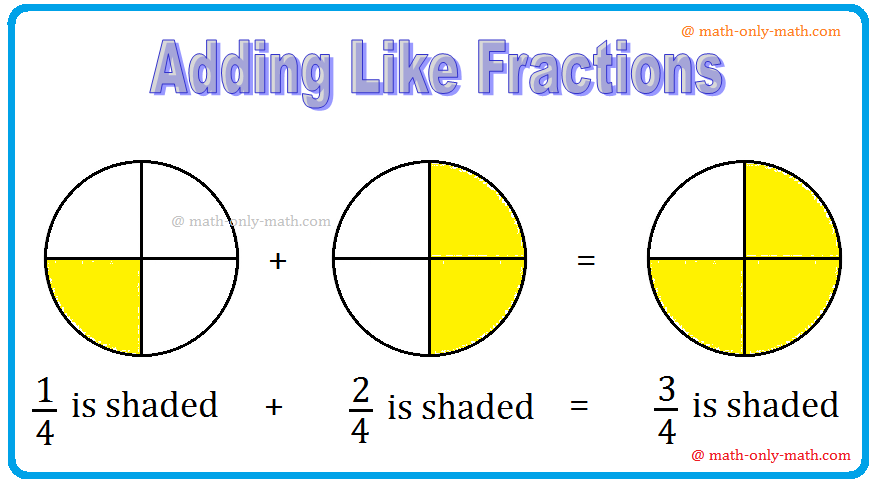
Addition of Like Fractions | Examples | Videos | Worksheet | Fractions
Apr 23, 25 09:23 AM
To add two or more like fractions we simplify add their numerators. The denominator remains same. Thus, to add the fractions with the same denominator, we simply add their numerators and write the com… -
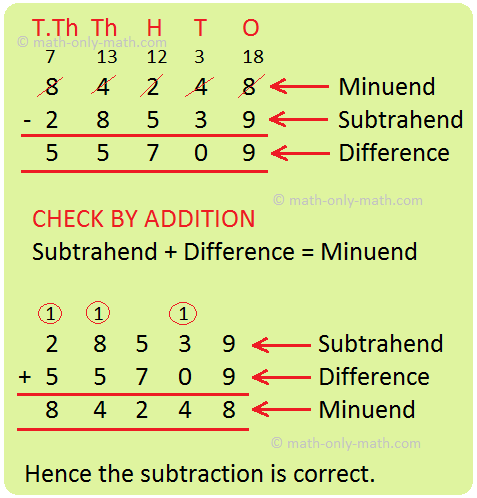
Subtraction | How to Subtract 2-digit, 3-digit, 4-digit Numbers?|Steps
Apr 23, 25 12:41 AM
The answer of a subtraction sum is called DIFFERENCE. How to subtract 2-digit numbers? Steps are shown to subtract 2-digit numbers. -
Subtraction of 4-Digit Numbers | Subtract Numbers with Four Digit
Apr 23, 25 12:38 AM
We will learn about the subtraction of 4-digit numbers (without borrowing and with borrowing). We know when one number is subtracted from another number the result obtained is called the difference. -
Subtraction with Regrouping | 4-Digit, 5-Digit and 6-Digit Subtraction
Apr 23, 25 12:34 AM
We will learn subtraction 4-digit, 5-digit and 6-digit numbers with regrouping. Subtraction of 4-digit numbers can be done in the same way as we do subtraction of smaller numbers. We first arrange the…




New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.