Circle Touches both x-axis and y-axis

We will learn how to find the equation of a circle touches both x-axis and y-axis.

The equation of a circle with centre at (h, k) and radius equal to a, is (x - h)\(^{2}\) + (y - k)\(^{2}\) = a\(^{2}\).

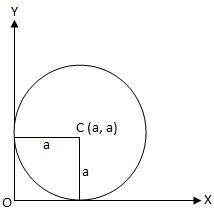
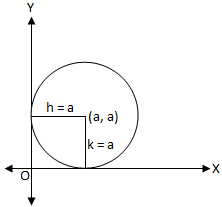
When the circle touches both x-axis and y-axis i.e., h = k = a.

Then the equation (x - h)\(^{2}\) + (y - k)\(^{2}\) = a\(^{2}\) becomes (x - a)\(^{2}\) + (y - a)\(^{2}\) = a\(^{2}\)

Circle Touches both x-axis and y-axis

Circle Touches both the x-axis and y-axis

If a circle touches both the co-ordinate axes then the abscissa as well as ordinate of the centre will be equal to the radius of the circle. Hence, the equation of the circle will be of the form:

(x - a)\(^{2}\) + (y - a)\(^{2}\) = a\(^{2}\)

⇒ x\(^{2}\) + y\(^{2}\) - 2ax - 2ay + a\(^{2}\) = 0

Solved example on the central form of the equation of a circle touches both x-axis and y-axis:

1. Find the equation of a circle whose radius is 4 units and touches both x-axis and y-axis.

Solution:

Radius of the circle = 4 units.

Since, the circle touches both x-axis and y-axis the centre of the circle is (4, 4).

The required equation of the circle whose radius is 4 units and touches both x-axis and y-axis is

(x - 4)\(^{2}\) + (y - 4)\(^{2}\) = 4\(^{2}\)

⇒ x\(^{2}\) - 8x + 16 + y\(^{2}\) - 8y + 16 = 16

⇒ x\(^{2}\) - 8x - 8y + 16 = 0

2. Find the equation of a circle whose radius is 8 units and touches both x-axis and y-axis.

Solution:

Radius of the circle = 8 units.

Since, the circle touches both x-axis and y-axis the centre of the circle is (8, 8).

The required equation of the circle whose radius is 8 units and touches both x-axis and y-axis is

(x - 8)\(^{2}\) + (y - 8)\(^{2}\) = 8\(^{2}\)

⇒ x\(^{2}\) - 16x + 64 + y\(^{2}\) - 16y + 64 = 64

⇒ x\(^{2}\) + y\(^{2}\) - 16x - 16y + 64 = 0

● The Circle

• Definition of Circle
• Equation of a Circle
• General Form of the Equation of a Circle
• General Equation of Second Degree Represents a Circle
• Centre of the Circle Coincides with the Origin
• Circle Passes through the Origin
• Circle Touches x-axis
• Circle Touches y-axis
• Circle Touches both x-axis and y-axis
• Centre of the Circle on x-axis
• Centre of the Circle on y-axis
• Circle Passes through the Origin and Centre Lies on x-axis
• Circle Passes through the Origin and Centre Lies on y-axis
• Equation of a Circle when Line Segment Joining Two Given Points is a Diameter
• Equations of Concentric Circles
  
• Circle Passing Through Three Given Points
• Circle Through the Intersection of Two Circles
• Equation of the Common Chord of Two Circles
• Position of a Point with Respect to a Circle
• Intercepts on the Axes made by a Circle
• Circle Formulae
• Problems on Circle

11 and 12 Grade Math 

From Circle Touches both x-axis and y-axis to HOME PAGE