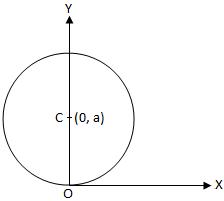
Circle Passes through the Origin and Centre Lies on y-axis
We will learn how to find the equation of a circle passes through the origin and centre lies on y-axis.
The equation of a circle with centre at (h, k) and radius equal to a, is (x - h)2 + (y - k)2 = a2.
When the circle passes through the origin and centre lies on x-axis i.e., h = 0 and k = a.
Then the equation (x - h)2 + (y - k)2 = a2 becomes x2 + (y - a)2 = a2
If a circle passes through the origin and centre lies on y-axis then the y co-ordinate will be equal to the radius of the circle and the abscissa of the centre will be zero. Hence, the equation of the circle will be of the form:
x2 + (y - a)2 = a2
⇒ x2 + y2 - 2ay = 0
Solved example on
the central form of the equation of a circle passes through the origin and
centre lies on y-axis:
1. Find the equation of a circle passes through the origin and centre lies on y-axis at (0, -6).
Solution:
Centre of the lies on x-axis at (0, -6)
Since, circle passes through the origin and centre lies on y-axis then the y co-ordinate will be equal to the radius of the circle and the abscissa of the centre will be zero.
The required equation of the circle passes through the origin and centre lies on y-axis at (0, -6) is
x2 + (y + 6)2 = (-6)2
⇒ x2 + y2 + 12y + 36 = 36
⇒ x2 + y2 + 12y = 0
2. Find the equation of a circle passes through the origin and centre lies on y-axis at (0, 20).
Solution:
Centre of the lies on y-axis at (0, 20)
Since, circle passes through the origin and centre lies on y-axis then the y co-ordinate will be equal to the radius of the circle and the abscissa of the centre will be zero.
The required equation of the circle passes through the origin and centre lies on y-axis at (0, 20) is
x2 + (y - 20)2 = 202
⇒ x2 + y2 - 40y + 400 = 400
⇒ x2 + y2 - 40y = 0
● The Circle
- Definition of Circle
- Equation of a Circle
- General Form of the Equation of a Circle
- General Equation of Second Degree Represents a Circle
- Centre of the Circle Coincides with the Origin
- Circle Passes through the Origin
- Circle Touches x-axis
- Circle Touches y-axis
- Circle Touches both x-axis and y-axis
- Centre of the Circle on x-axis
- Centre of the Circle on y-axis
- Circle Passes through the Origin and Centre Lies on x-axis
- Circle Passes through the Origin and Centre Lies on y-axis
- Equation of a Circle when Line Segment Joining Two Given Points is a Diameter
- Equations of Concentric Circles
- Circle Passing Through Three Given Points
- Circle Through the Intersection of Two Circles
- Equation of the Common Chord of Two Circles
- Position of a Point with Respect to a Circle
- Intercepts on the Axes made by a Circle
- Circle Formulae
- Problems on Circle
11 and 12 Grade Math
From Circle Passes through the Origin and Centre Lies on y-axis to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Converting Fractions to Decimals | Solved Examples | Free Worksheet
Apr 28, 25 01:43 AM
In converting fractions to decimals, we know that decimals are fractions with denominators 10, 100, 1000 etc. In order to convert other fractions into decimals, we follow the following steps: -
Expanded Form of a Number | Writing Numbers in Expanded Form | Values
Apr 27, 25 10:13 AM
We know that the number written as sum of the place-values of its digits is called the expanded form of a number. In expanded form of a number, the number is shown according to the place values of its… -
Converting Decimals to Fractions | Solved Examples | Free Worksheet
Apr 26, 25 04:56 PM
In converting decimals to fractions, we know that a decimal can always be converted into a fraction by using the following steps: Step I: Obtain the decimal. Step II: Remove the decimal points from th… -
Worksheet on Decimal Numbers | Decimals Number Concepts | Answers
Apr 26, 25 03:48 PM
Practice different types of math questions given in the worksheet on decimal numbers, these math problems will help the students to review decimals number concepts. -
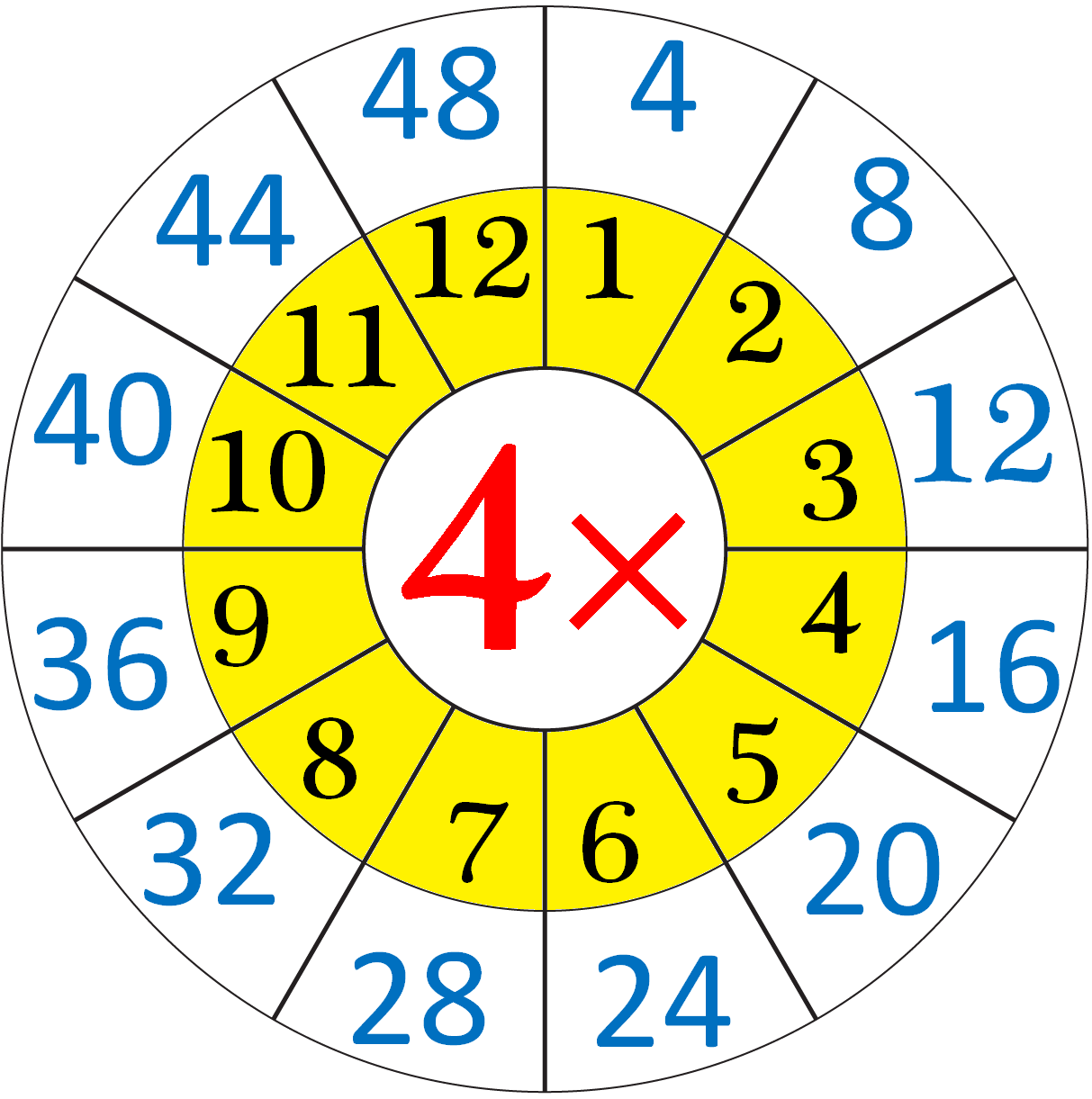
Multiplication Table of 4 |Read and Write the Table of 4|4 Times Table
Apr 26, 25 01:00 PM
Repeated addition by 4’s means the multiplication table of 4. (i) When 5 candle-stands having four candles each. By repeated addition we can show 4 + 4 + 4 + 4 + 4 = 20 Then, four 5 times



New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.