Changing Fractions
In changing fractions we will discuss how to change fractions from
improper fraction to a whole or mixed number, from mixed number to an
improper fraction, from whole number into an improper fraction.
Changing an improper fraction to a whole number or mixed number:
Here we will learn about changing an improper fraction to a whole or mixed number.
Cut out three circle of the same size.
Fold each circle in four.
Shade 4 parts from the first circle, 4 parts from the second circle and one part from the third circle.
Total parts shaded = 9 we have 9/4 parts.
Total parts in each circle 4 which is really 2
1/
4 parts.
Note:
When the numerator of a
fraction is greater than the denominator, the fraction is greater than
1. This can be written as mixed number.
Changing improper fractions to mixed numbers by dividing the numerator with the denominator.
1. 9/4
= 2
1/
4
Therefore,
9/
4 = 2
1/
4
2. 24/10 Try to reduce the numerator and denominator by a common denominator.
24/10 ÷ 2/2 = 12/5
Now divide numerator by denominator.
= 2
2/
5
|
Improper fraction
24/10
|
Mixed number
22/5
|
Sometimes an improper fraction change into a whole number when there is no remainder.
3. 16/2 ÷ 2/2 = 8/1 = 8
Note:
When the denominator is 1 in an improper fraction, it becomes a whole number.
Changing a mixed number to an improper fraction:
Mother said I had eaten 3
1/
2 chocolates.
This is what I took :
1/
2 +
1/
2 +
1/
2 +
1/
2 +
1/
2 +
1/
2 +
1/
2 = 7 halves
=
7/
2
But I looked carefully. I had eaten 3 full + 1/2 chocolate.
Let us learn the mathematical way of changing mixed numbers to improper fractions.
Mixed numbers Denominator × Whole numbers Numerator
5
1/
2 = 2 × 5 + 1 =
11/
2
Multiply denominator and whole number 5.
2 × 5 = 10
|
Mixed numbers
51/2
|
Improper fraction
11/2
|
Add the numerator 10 + 1 = 11
This becomes the new numerator.
The old denominator remains.
Changing a whole number into an improper fraction:
|
Whole number
7
|
Improper fraction
7/1
|
Since the denominator shows total parts and anything whole is out of 1
part, the improper fraction is formed by using 1 as the denominator.
1. Convert the given fractions to mixed fractions:
(i) \(\frac{11}{2}\)
(ii) \(\frac{15}{9}\)
(iii) \(\frac{25}{4}\)
(iv) \(\frac{57}{7}\)
Answers:
1. (i) 5\(\frac{1}{2}\)
(ii) 1\(\frac{6}{9}\)
(iii) 6\(\frac{1}{4}\)
(iv) 8\(\frac{1}{7}\)
2. Convert the given mixed fractions to improper fractions:
(i) 3\(\frac{5}{6}\)
(ii) 7\(\frac{2}{9}\)
(iii) 5\(\frac{3}{4}\)
(iv) 8\(\frac{2}{3}\)
Answers:
2. (i) \(\frac{23}{6}\)
(ii) \(\frac{65}{9}\)
(iii) \(\frac{23}{4}\)
(iv) \(\frac{26}{3}\)
You might like these
-
To add two or more like fractions we simplify add their numerators. The denominator remains same.
-
In worksheet on addition of fractions having the same denominator, all grade students can practice the questions on adding fractions. This exercise sheet on fractions can be practiced by the students to get more ideas how to add fractions with the same denominators.
-
In worksheet on subtraction of fractions having the same denominator, all grade students can practice the questions on subtracting fractions. This exercise sheet on fractions can be practiced by the students to get more ideas how to subtract fractions with the same
-
Addition and subtraction of like fractions. Addition of Like Fractions: To add two or more like fractions we simplify add their numerators. The denominator remains same. To subtract two or more like fractions we simply subtract their numerators and keep the same denominator.
-
Recall the topic carefully and practice the questions given in the math worksheet on add and subtract fractions. The question mainly covers addition with the help of a fraction number line, subtraction with the help of a fraction number line, add the fractions with the same
-
In 4th grade fractions worksheet we will circle the like fractions, circle the greatest fraction, arrange the fractions in descending order, arrange the fractions in ascending order, addition of like fractions and subtraction of like fractions.
-
We will discuss here how to arrange the fractions in ascending order. Solved examples for arranging in ascending order: 1. Arrange the following fractions 5/6, 8/9, 2/3 in ascending order. First we find the L.C.M. of the denominators of the fractions to make the denominators
-
In comparison of unlike fractions, we change the unlike fractions to like fractions and then compare. To compare two fractions with different numerators and different denominators, we multiply by a number to convert them to like fractions. Let us consider some of the
-
Any two like fractions can be compared by comparing their numerators. The fraction with larger numerator is greater than the fraction with smaller numerator, for example \(\frac{7}{13}\) > \(\frac{2}{13}\) because 7 > 2. In comparison of like fractions here are some
-
Like and unlike fractions are the two groups of fractions: (i) 1/5, 3/5, 2/5, 4/5, 6/5 (ii) 3/4, 5/6, 1/3, 4/7, 9/9 In group (i) the denominator of each fraction is 5, i.e., the denominators of the fractions are equal. The fractions with the same denominators are called
-
In worksheet on equivalent fractions, all grade students can practice the questions on equivalent fractions. This exercise sheet on equivalent fractions can be practiced by the students to get more ideas to change the fractions into equivalent fractions.
-
We will discuss here about verification of equivalent fractions. To verify that two fractions are equivalent or not, we multiply the numerator of one fraction by the denominator of the other fraction. Similarly, we multiply the denominator of one fraction by the numerator
-
Equivalent fractions are the fractions having the same value. An equivalent fraction of a given fraction can be obtained by multiplying its numerator and denominator by the same number
-
In 5th Grade Fractions Worksheets we will solve how to compare two fractions, comparing mixed fractions, addition of like fractions, addition of unlike fractions, addition of mixed fractions, word problems on addition of fractions, subtraction of like fractions
-
Here we will learn Reciprocal of a fraction. What is 1/4 of 4? We know that 1/4 of 4 means 1/4 × 4, let us use the rule of repeated addition to find 1/4× 4. We can say that \(\frac{1}{4}\) is the reciprocal of 4 or 4 is the reciprocal or multiplicative inverse of 1/4
-
To divide a fraction or a whole number by a fraction or a whole number, we multiply the reciprocal of the divisor. We know that the reciprocal or the multiplicative inverse of 2 is \(\frac{1}{2}\).
-
Here we will learn fraction of a fraction. Let us look at the picture of a chocolate bar. The chocolate bar has 6 parts in it. Each part of the chocolate is equal to \(\frac{1}{6}\). Sharon wants to eat1/2 of one chocolate part. What is 1/2 of 1/6?
-
To multiply two or more fractions, we multiply the numerators of given fractions to find the new numerator of the product and multiply the denominators to get the denominator of the product. To multiply a fraction by a whole number, we multiply the numerator of the fraction
-
To subtract unlike fractions, we first convert them into like fractions. In order to make a common denominator, we find LCM of all the different denominators of given fractions and then make them equivalent fractions with a common denominators.
-
We will learn how to solve subtraction of mixed fractions or subtraction of mixed numbers. There are two methods to subtract the mixed fractions. Step I: Subtract the whole numbers. Step II: To subtract the fractions we convert them into like fractions. Step III: Add the
Related Concept
4th Grade Math Activities
From Changing Fractions to HOME PAGE
Didn't find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.
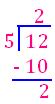
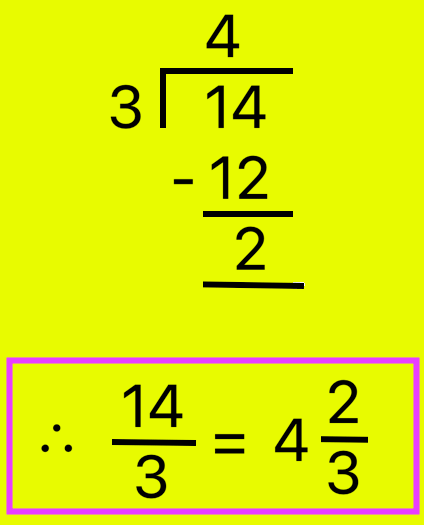
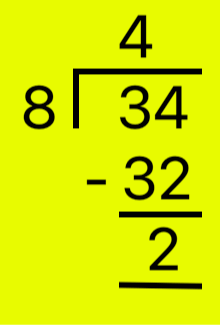
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.