Area of a Trapezium

In area of a trapezium we will discuss about the formula and the solved examples in area of a trapezium.

Trapezium:

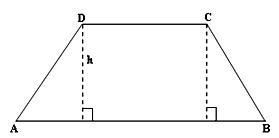
A trapezium is a quadrilateral having one pair of parallel opposite sides. In the given figure, ABCD is a trapezium in which AB ∥ DC.

Area of a Trapezium:

Let ABCD be a trapezium in which AB ∥ DC, CE ⊥ AB, DF ⊥ AB and CE = DF = h. 

Prove that:

Area of a trapezium ABCD = {¹/₂ × (AB + DC) × h} square units.

Proof:     Area of a trapezium ABCD

            = area (∆DFA) + area (rectangle DFEC) + area (∆CEB)

            = (¹/₂ × AF × DF) + (FE × DF) + (¹/₂ × EB × CE)

           = (¹/₂ × AF × h) + (FE × h) + (¹/₂ × EB × h)

            = ¹/₂ × h × (AF + 2FE + EB)

            = ¹/₂ × h × (AF + FE + EB + FE)

            = ¹/₂ × h × (AB + FE)

            = ¹/₂ × h × (AB + DC) square units.

            = ¹/₂ × (sum of parallel sides) × (distance between them)

Formula of Area of a trapezium = ¹/₂ × (sum of parallel sides) × (distance between them)

Solved Examples of Area of a Trapezium

1. Two parallel sides of a trapezium are of lengths 27 cm and 19 cm respectively, and the distance between them is 14 cm. Find the area of the trapezium.

Solution: 

Area of the trapezium

      = ¹/₂ × (sum of parallel sides) × (distance between them) 

      = {¹/₂ × (27 + 19) × 14} cm²

      = 322 cm²

2. The area of a trapezium is 352 cm² and the distance between its parallel sides is 16 cm. If one of the parallel sides is of length 25 cm, find the length of the other.

Solution: 

Let the length of the required side be x cm. 

Then, area of the trapezium = {¹/₂ × (25 + x) × 16} cm² 

                                              = (200 + 8x) cm². 

But, the area of the trapezium = 352 cm² (given) 

Therefore, 200 + 8x = 352 

                ⇒ 8x = (352 - 200) 

                ⇒ 8x = 152 

                ⇒ x = (152/8) 

                ⇒ x = 19. 

Hence, the length of the other side is 19 cm. 

3. The parallel sides of a trapezium are 25 cm and 13 cm; its nonparallel sides are equal, each being 10 cm. Find the area of the trapezium.

Solution:

Let ABCD be the given trapezium in which AB = 25 cm, DC = 13 cm, BC = 10 cm and AD = 10 cm.

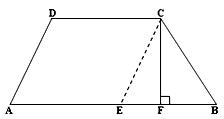
Through C, draw CE ∥ AD, meeting AB at E.

Also, draw CF ⊥ AB.

Now, EB = (AB - AE) = (AB - DC)

              = (25 - 13) cm = 12 cm;

        CE = AD = 10 cm; AE = DC = 13 cm.

Now, in ∆EBC, we have CE = BC = 10 cm.

So, it is an isosceles triangle.

Also, CF ⊥ AB

So, F is the midpoint of EB.

Therefore, EF = ¹/₂ × EB = 6cm.

Thus, in right-angled ∆CFE, we have CE = 10 cm, EF = 6 cm.

By Pythagoras’ theorem, we have

CF = [√CE² - EF²]

     = √(10² - 6²)

     = √64

     = √(8 × 8)

     = 8 cm.

Thus, the distance between the parallel sides is 8 cm.

Area of trapezium ABCD = ¹/₂ × (sum of parallel sides) × (distance between them)

                                        = {¹/₂ × (25 + 13) × 8 cm²

                                        = 152 cm²

4. ABCD is a trapezium in which AB ∥ DC, AB = 78 cm, CD = 52 cm, AD = 28 cm and BC = 30 cm. Find the area of the trapezium.

Solution:

Draw CE ∥ AD and CF ⊥ AB.

Now, EB = (AB - AE) = (AB - DC) = (78 - 52) cm = 26 cm,

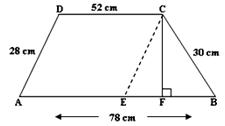
CE = AD = 28 cm and BC = 30 cm.

Now, in ∆CEB, we have

S = ¹/₂ (28 + 26 + 30) cm = 42 cm.

(s - a) = (42 - 28) cm = 14 cm,

(s - b) = (42 - 26) cm = 16 cm, and

(s - c) = (42 - 30) cm = 12 cm.

area of ∆CEB = √{s(s - a)(s - b)(s - c)}

                      = √(42 × 14 × 16 × 12) cm²

                      = 336 cm²

Also, area of ∆CEB = ¹/₂ × EB × CF

                               = (¹/₂ × 26 × CF) cm²

                               = (13 × CF) cm²

Therefore, 13 × CF = 336

⇒ CF = 336/13 cm

Area of a trapezium ABCD

                    = {¹/₂ × (AB + CD) × CF} square units

                    = {¹/₂ × (78 + 52) × ³³⁶/₁₃} cm²

                    = 1680 cm²

● Area of a Trapezium

Area of a Trapezium

Area of a Polygon

● Area of a Trapezium - Worksheet

Worksheet on Trapezium

Worksheet on Area of a Polygon

8th Grade Math Practice 

From Area of a Trapezium to HOME PAGE