Area and Perimeter of a Semicircle and Quadrant of a Circle

We will learn how to find the Area and perimeter of a semicircle and Quadrant of a circle.

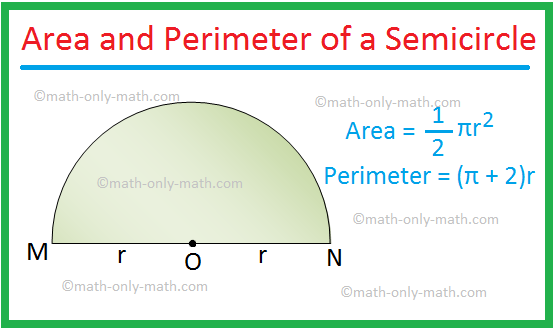
Area of a semicircle = $\frac{1}{2}$πr²

Perimeter of a semicircle = (π + 2)r.

because a semicircle is a sector of sectorial angle 180°.

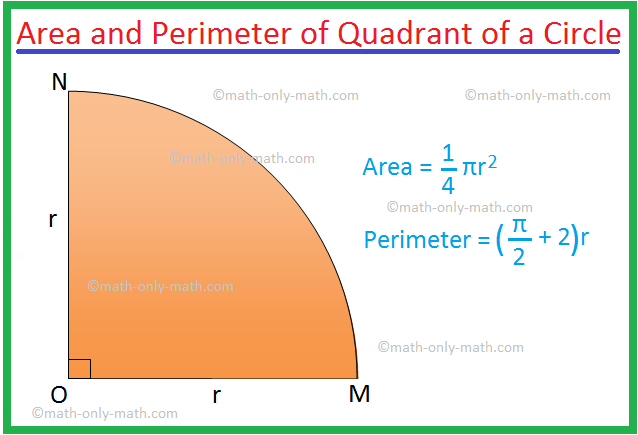
Area of a quadrant of a circle = $\frac{1}{4}$πr².

Perimeter of a quadrant of a circle = ($\frac{π}{2}$ + 2)r.

because a quadrant of a circle is a sector of the circle whose sectorial angle is 90°.

Here r is the radius of the circle.

Solved Examples on Area and perimeter of a semicircle and Quadrant of a circle:

1. The area of a semicircular region is 308 cm^2. Find its perimeter. (Use π = $\frac{22}{7}$.)

Solution:

Let r be the radius. Then,

area = $\frac{1}{2}$ ∙ πr^2

⟹ 308 cm^2 = $\frac{1}{2}$ ∙ $\frac{22}{7}$ ∙ r^2

⟹ 308 cm^2 = $\frac{22}{14}$ ∙ r^2

⟹ $\frac{22}{14}$ ∙ r^2 = 308 cm^2

⟹ r^2 = $\frac{14}{22}$ ∙ 308 cm^2

⟹ r^2 = $\frac{7}{11}$ ∙ 308 cm^2

⟹ r^2 = 7 × 28 cm^2

⟹ r^2 = 196 cm^2

⟹ r^2 = 14^2 cm^2

⟹ r = 14 cm.

Therefore, the radius of the circle is 14 cm.

Now, perimeter = (π + 2)r

                       = ($\frac{22}{7}$ + 2) ∙ 14 cm

                       = $\frac{36}{7}$  ×  14 cm

                       = 36 × 2 cm

                       = 72 cm.

2. The perimeter of a sheet of paper in the shape of a quadrant of a circle is 75 cm. Find its area. (Use π = $\frac{22}{7}$.)

Solution:

Let the radius be r. 

Then,

perimeter = ($\frac{π}{2}$ + 2)r

⟹ 75 cm = ($\frac{1}{2}$ ∙ π + 2)r

⟹ 75 cm = ($\frac{ 1 }{2}$ ∙ $\frac{22}{7}$  + 2)r

⟹ 75 cm = ($\frac{11}{7}$  + 2)r

⟹ 75 cm = $\frac{25}{7}$r

⟹ $\frac{25}{7}$r = 75 cm

⟹ r = 75 × $\frac{7}{25}$ cm

⟹ r = 3 × 7 cm

⟹ r = 21 cm.

Therefore, the radius of the circle is 21 cm.

Now, area = $\frac{1}{4}$πr^2

                = $\frac{1}{4}$ ∙  $\frac{22}{7}$ ∙ 21^2 cm^2

                = $\frac{1}{4}$ ∙  $\frac{22}{7}$ ∙ 21 ∙ 21 cm^2

                = $\frac{693}{2}$ cm^2

                = 346.5 cm^2.

Therefore, area of the sheet of paper is 346.5 cm^2.

10th Grade Math

From Area and Perimeter of a Semicircle and Quadrant of a Circle to HOME PAGE

New! Comments

Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.

Share this page: What’s this?

FacebookXPinterestWhatsAppReddit

ShareFacebookXPinterestWhatsAppReddit