arcsin(x) + arccos(x) = \(\frac{π}{2}\)
We will learn how to prove the property of the inverse trigonometric function arcsin(x) + arccos(x) = \(\frac{π}{2}\).
Proof: Let, sin\(^{-1}\) x = θ
Therefore, x = sin θ
x = cos (\(\frac{π}{2}\) - θ), [Since, cos (\(\frac{π}{2}\) - θ) = sin θ]
⇒ cos\(^{-1}\) x = \(\frac{π}{2}\) - θ
⇒ cos\(^{-1}\) x= \(\frac{π}{2}\) - sin\(^{-1}\) x, [Since, θ = sin\(^{-1}\) x]
⇒ sin\(^{-1}\) x + cos\(^{-1}\) x = \(\frac{π}{2}\)
Therefore, sin\(^{-1}\) x + cos\(^{-1}\) x = \(\frac{π}{2}\). Proved.
Solved examples on property of inverse circular
function sin\(^{-1}\)
x + cos\(^{-1}\) x
=
\(\frac{π}{2}\).
1. Prove that sin\(^{-1}\) \(\frac{4}{5}\) + sin\(^{-1}\) \(\frac{5}{13}\) + sin\(^{-1}\) \(\frac{16}{65}\) = \(\frac{π}{2}\)
Solution:
sin\(^{-1}\) \(\frac{4}{5}\) + sin\(^{-1}\) \(\frac{5}{13}\) + sin\(^{-1}\) \(\frac{16}{65}\)
= (sin\(^{-1}\) \(\frac{4}{5}\) + sin\(^{-1}\) \(\frac{5}{13}\)) + sin\(^{-1}\) \(\frac{16}{65}\)
= \(sin^{-1}(\frac{4}{5}\sqrt{1 - (\frac{5}{13})^{2}}) + \frac{5}{13}\sqrt{1 - (\frac{4}{5})^{2}})\) + sin\(^{-1}\) \(\frac{16}{65}\)
= sin\(^{-1}\) (\(\frac{4}{5}\) × \(\frac{12}{13}\) + \(\frac{5}{13}\) × \(\frac{3}{5}\)) + sin\(^{-1}\) \(\frac{16}{65}\)
= sin\(^{-1}\) \(\frac{63}{65}\) + sin\(^{-1}\) \(\frac{16}{65}\)
= \(cos^{-1}\sqrt{1 - (\frac{63}{65})^{2}})\) + sin\(^{-1}\) \(\frac{16}{65}\)
= cos\(^{-1}\) \(\frac{16}{65}\) + sin\(^{-1}\) \(\frac{16}{65}\)
= π/2, since \(sin^{-1} x + cos^{-1} x = \frac{π}{2}\)
Therefore, sin\(^{-1}\) \(\frac{4}{5}\) + sin\(^{-1}\) \(\frac{5}{13}\) + sin\(^{-1}\) \(\frac{16}{65}\) = \(\frac{π}{2}\). Proved.
2. Solve the trigonometric equation: sin\(^{-1}\) \(\frac{5}{x}\) + sin\(^{-1}\) \(\frac{12}{x}\) = \(\frac{π}{2}\)
Solution:
sin\(^{-1}\) \(\frac{5}{x}\) + sin\(^{-1}\) \(\frac{12}{x}\) = \(\frac{π}{2}\)
⇒ sin\(^{-1}\) \(\frac{12}{x}\) = \(\frac{π}{2}\) - sin\(^{-1}\) \(\frac{5}{x}\)
⇒ sin\(^{-1}\) \(\frac{12}{x}\) = cos\(^{-1}\) \(\frac{5}{x}\), [Since, we know that, sin\(^{-1}\) \(\frac{5}{x}\) + cos\(^{-1}\) \(\frac{5}{x}\) = \(\frac{π}{2}\)]
⇒ sin\(^{-1}\) \(\frac{12}{x}\) = sin\(^{-1}\) \(\frac{\sqrt{x^{2} - 25}}{x}\)
⇒ \(\frac{12}{x}\) = \(\frac{\sqrt{x^{2} - 25}}{x}\)
⇒ \(\sqrt{x^{2} - 25}\) = 12, [Since, x ≠ 0]
⇒ x\(^{2}\) - 25 = 144
⇒ x\(^{2}\) = 144 + 25
⇒ x\(^{2}\) = 169
⇒ x = ± 13
The solution x = - 13 does not satisfy the given equation.
Therefore the required solution is x = 13.
● Inverse Trigonometric Functions
- General and Principal Values of sin\(^{-1}\) x
- General and Principal Values of cos\(^{-1}\) x
- General and Principal Values of tan\(^{-1}\) x
- General and Principal Values of csc\(^{-1}\) x
- General and Principal Values of sec\(^{-1}\) x
- General and Principal Values of cot\(^{-1}\) x
- Principal Values of Inverse Trigonometric Functions
- General Values of Inverse Trigonometric Functions
- arcsin(x) + arccos(x) = \(\frac{π}{2}\)
- arctan(x) + arccot(x) = \(\frac{π}{2}\)
- arctan(x) + arctan(y) = arctan(\(\frac{x + y}{1 - xy}\))
- arctan(x) - arctan(y) = arctan(\(\frac{x - y}{1 + xy}\))
- arctan(x) + arctan(y) + arctan(z)= arctan\(\frac{x + y + z – xyz}{1 – xy – yz – zx}\)
- arccot(x) + arccot(y) = arccot(\(\frac{xy - 1}{y + x}\))
- arccot(x) - arccot(y) = arccot(\(\frac{xy + 1}{y - x}\))
- arcsin(x) + arcsin(y) = arcsin(x \(\sqrt{1 - y^{2}}\) + y\(\sqrt{1 - x^{2}}\))
- arcsin (x) - arcsin(y) = arcsin (x \(\sqrt{1 - y^{2}}\) - y\(\sqrt{1 - x^{2}}\))
- arccos (x) + arccos(y) = arccos(xy - \(\sqrt{1 - x^{2}}\)\(\sqrt{1 - y^{2}}\))
- arccos(x) - arccos(y) = arccos(xy + \(\sqrt{1 - x^{2}}\)\(\sqrt{1 - y^{2}}\))
- 2 arcsin(x) = arcsin(2x\(\sqrt{1 - x^{2}}\))
- 2 arccos(x) = arccos(2x\(^{2}\) - 1)
- 2 arctan(x) = arctan(\(\frac{2x}{1 - x^{2}}\)) = arcsin(\(\frac{2x}{1 + x^{2}}\)) = arccos(\(\frac{1 - x^{2}}{1 + x^{2}}\))
- 3 arcsin(x) = arcsin(3x - 4x\(^{3}\))
- 3 arccos(x) = arccos(4x\(^{3}\) - 3x)
- 3 arctan(x) = arctan(\(\frac{3x - x^{3}}{1 - 3 x^{2}}\))
- Inverse Trigonometric Function Formula
- Principal Values of Inverse Trigonometric Functions
- Problems on Inverse Trigonometric Function
11 and 12 Grade Math
From arcsin x + arccos x = π/2 to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Patterns in Numbers | Patterns in Maths |Math Patterns|Series Patterns
Feb 01, 25 12:56 AM
We see so many patterns around us in our daily life. We know that a pattern is an arrangement of objects, colors, or numbers placed in a certain order. Some patterns neither grow nor reduce but only r… -
Line Symmetry | Vertical & Horizontal Lines of Symmetry | Symmetrical
Feb 01, 25 12:45 AM
Line symmetry is discussed here. We know that any object or shape which can be cut in two equal halves in such a way that both the parts are exactly the same is called symmetrical and the line which d… -
Symmetrical Shapes | One, Two, Three, Four & Many-line Symmetry
Jan 31, 25 11:20 PM
Symmetrical shapes are discussed here in this topic. Any object or shape which can be cut in two equal halves in such a way that both the parts are exactly the same is called symmetrical. The line whi… -
Divide by Repeated Subtraction | Division as Repeated Subtraction
Jan 31, 25 11:10 PM
How to divide by repeated subtraction? We will learn how to find the quotient and remainder by the method of repeated subtraction a division problem may be solved. -
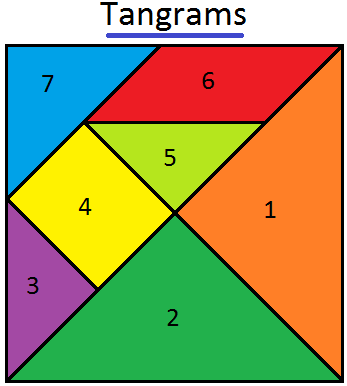
Tangrams Math | Traditional Chinese Geometrical Puzzle | Triangles
Jan 31, 25 02:42 PM
Tangram is a traditional Chinese geometrical puzzle with 7 pieces (1 parallelogram, 1 square and 5 triangles) that can be arranged to match any particular design. In the given figure, it consists of o…



New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.