Angle Angle Side Congruence
Conditions for the AAS – Angle Angle Side congruence
Two triangles are said to be congruent if two angles and non- included side of the one triangle is equal to the two angles and the non- included side of the other.
Experiment to prove Congruence with AAS:
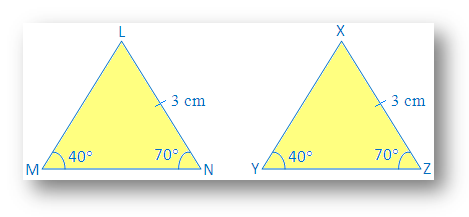
Draw a ∆LMN with ∠M = 40°, ∠N = 70°, LN = 3 cm.
Also, draw another ∆XYZ with ∠Y = 40°, ∠Z = 70°, XZ = 3cm.
We see that ∠M = ∠Y, ∠N = ∠Z and LN = XZ
Make a trace copy of ∆XYZ and try to make it cover LMN with X on L, Y on M and Z on N. Two triangles cover each other exactly.
Therefore ∆LMN ≅ ∆XYZ
Note:
Angle Angle Side (AAS) and Angle Side Angle (ASA) are more or less the same congruence condition.
Worked-out problems on angle angle side congruence triangles (AAS postulate):
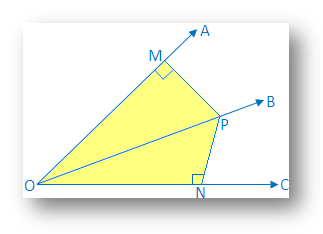
1. OB is the bisector of ∠AOC, PM ┴ OA and PN ┴ OC. Show that ∆MPO ≅ ∆NPO.
Solution:
In ∆MPO and ∆NPO
PM ┴ OM and PN ┴ ON
Therefore ∠PMO = ∠PNO = 90°
Also, OB is the bisector of ∠AOC
Therefore ∠MOP = ∠NOP
OP = OP common
Therefore, ∆MPO ≅ ∆NPO by AAS congruence condition
Conditions for the Congruence of Triangles
Right Angle Hypotenuse Side congruence
Converse of Pythagorean Theorem
7th Grade Math Problems
8th Grade Math Practice
From Angle Angle Side Congruence to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Worksheet on Comparing and Ordering Decimals |Arranging Decimals
Apr 19, 25 12:16 PM
Practice different types of math questions given in the worksheet on comparing and ordering decimals. This worksheet contains questions mainly related to compare decimals and then place the decimals i… -
Comparison of Decimal Fractions | Comparing Decimals Numbers | Decimal
Apr 19, 25 11:47 AM
While comparing natural numbers we first compare total number of digits in both the numbers and if they are equal then we compare the digit at the extreme left. If they also equal then we compare the… -
Expanded form of Decimal Fractions |How to Write a Decimal in Expanded
Apr 19, 25 11:25 AM
Decimal numbers can be expressed in expanded form using the place-value chart. In expanded form of decimal fractions we will learn how to read and write the decimal numbers. Note: When a decimal is mi… -
Missing Numbers up to 10 | Worksheets on Missing Numbers up to 10
Apr 18, 25 04:53 PM
Printable worksheets on missing numbers up to 10 help the kids to practice counting of the numbers. -
Ordering Decimals | Comparing Decimals | Ascending & Descending Order
Apr 18, 25 01:49 PM
In ordering decimals we will learn how to compare two or more decimals. (i) Convert each of them as like decimals. (ii) Compare these decimals just as we compare two whole numbers ignoring
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.