Worksheet on Matrix

In Worksheet on matrix the questions are based on finding unknown elements and matrices from matrix equation.

1. Let A = \(\begin{bmatrix} 1 & 2\\ 2 & 3 \end{bmatrix}\), B = \(\begin{bmatrix} 2 & 1\\ 3 & 2 \end{bmatrix}\) and C =  \(\begin{bmatrix} 1 & 3\\ 3 & 1 \end{bmatrix}\)

(i) Find the matrix C(B – A).

(ii) Find A(B + C).

(iii) Prove that A(B + C) = AB + AC.

2. If A =  \(\begin{bmatrix} 3 & 2\\ 1 & 0 \end{bmatrix}\), B =  \(\begin{bmatrix} -1 & 3\\ 0 & 1 \end{bmatrix}\) then verify the truth of the following.

(i) (A + B)2 = A2 + B2 + 2AB

(ii) (A + B)(A – B) = A2 – B2


3. If X =  \(\begin{bmatrix} 4 & 1\\ -1 & 2 \end{bmatrix}\), show that 6X – X2 = 9I, where I is the unit matrix.

4. (i) Show that X = \(\begin{bmatrix} 1 & 2\\ 2 & 1 \end{bmatrix}\) satisfies the relation X2 – 2X – 3I = O, where I is the unit matrix of order 2 × 2 and O is the null matrix of order 2 × 2.

(ii) Let A = \(\begin{bmatrix} 1 & 0\\ 2 & 1 \end{bmatrix}\), B = \(\begin{bmatrix} 2 & 3\\ -1 & 0 \end{bmatrix}\). Find A2 + AB + B2.


5. Find the matrix X from the matrix equation \(\begin{bmatrix} 2 & 1\\ 5 & 0 \end{bmatrix}\) – 3X = \(\begin{bmatrix} -7 & 4\\ 2 & 6 \end{bmatrix}\).

6. (i) If A = \(\begin{bmatrix} 1 & x\\ 0 & 1 \end{bmatrix}\) and \(\begin{bmatrix} 3 & 4\\ 5 & y \end{bmatrix}\) such that A + 2B = 5\(\begin{bmatrix} \frac{7}{5} & 0\\ 2 & 1 \end{bmatrix}\) then find x and y.

(ii) If 2\(\begin{bmatrix} 3 & 4\\ 5 & x \end{bmatrix}\) + \(\begin{bmatrix} 1 & y\\ 0 & 1 \end{bmatrix}\) = \(\begin{bmatrix} 7 & x\\ 10 & 5 \end{bmatrix}\), find x and y.


7. If \(\begin{bmatrix} 4\\ x\\ -y \end{bmatrix}\)\(\begin{bmatrix} 2 & 1 \end{bmatrix}\) = \(\begin{bmatrix} 8 & 4\\ 6 & 3\\ -8 & -4 \end{bmatrix}\), find x and y.

8. If \(\begin{bmatrix} 4 & -5\\ 6 & 7 \end{bmatrix}\)\(\begin{bmatrix} x\\ y \end{bmatrix}\) = \(\begin{bmatrix} -1\\ 2 \end{bmatrix}\), find x and y.

9. If \(\begin{bmatrix} 1 & 2\\ 3 & 3 \end{bmatrix}\)\(\begin{bmatrix} x & 0\\ 0 & y \end{bmatrix}\) = \(\begin{bmatrix} x & 0\\ 9 & 0 \end{bmatrix}\), find x and y.

10. If \(\begin{bmatrix} -3 & 2\\ 0 & -5 \end{bmatrix}\)\(\begin{bmatrix} x\\ 2 \end{bmatrix}\) = \(\begin{bmatrix} -5\\ y \end{bmatrix}\), find x and y.

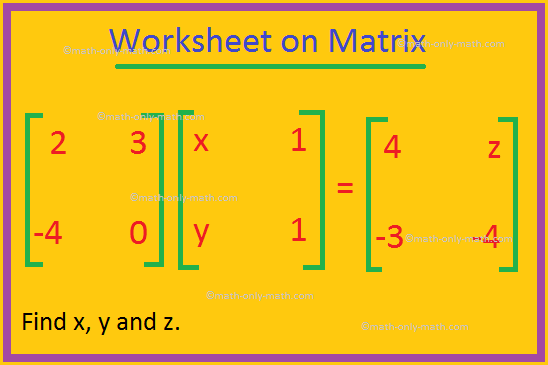
11. If \(\begin{bmatrix} 2 & 3\\ -4 & 0 \end{bmatrix}\)\(\begin{bmatrix} x & 1\\ y & 1 \end{bmatrix}\) = \(\begin{bmatrix} 4 & z\\ -3 & -4 \end{bmatrix}\), then find x, y and z.

Worksheet on Matrix

12. Let A = \(\begin{bmatrix} 2 & 12\\ 0 & 1 \end{bmatrix}\) and B = \(\begin{bmatrix} 4 & x\\ 0 & 1 \end{bmatrix}\). If A2 = B, find x.

13. Let A = \(\begin{bmatrix} 1 & 3\\ 1 & 3 \end{bmatrix}\) and B = \(\begin{bmatrix} 3 & a\\ b & 2 \end{bmatrix}\). If AB = O, where O is the null matrix, find a and b.

14. Find x and y if \(\begin{bmatrix} x & 3x\\ y & 4y \end{bmatrix}\)\(\begin{bmatrix} 2\\ 1 \end{bmatrix}\) = \(\begin{bmatrix} 5\\ 12 \end{bmatrix}\).

15. Let A = \(\begin{bmatrix} 2 & 1\\ 3 & 4 \end{bmatrix}\). Find the matrix B such that A2 = 2A + 3B.

16. Let A = \(\begin{bmatrix} 1 & -3\\ 2 & 4 \end{bmatrix}\), B = \(\begin{bmatrix} -1\\ 2 \end{bmatrix}\) and C is a matrix such that AC = B then find the matrix C.

17. Let A = \(\begin{bmatrix} 2 & 1\\ 3 & 4 \end{bmatrix}\). Find the matrix B such that AB = I, where I is the unit matrix of the order 2 × 2.

18. Given A = \(\begin{bmatrix} 2 & -1\\ 2 & 0 \end{bmatrix}\), B = \(\begin{bmatrix} -3 & 2\\ 4 & 0 \end{bmatrix}\) and C = \(\begin{bmatrix} 1 & 0\\ 0 & 2 \end{bmatrix}\). Find the matrix X such that A + X = 2B + C.

19. If \(\begin{bmatrix} 1 & 4\\ -2 & 3 \end{bmatrix}\) + 2M = 3\(\begin{bmatrix} 3 & 2\\ 0 & -3 \end{bmatrix}\), find the matrix M.

20. (i) Show that X = \(\begin{bmatrix} 1 & 2\\ 2 & 1 \end{bmatrix}\) satisfies the relation X2 – 2X – 3I = O, where I is the unit matrix of order 2 × 2 and O is the null matrix of order 2 × 2.

(ii) Let A = \(\begin{bmatrix} 1 & 0\\ 2 & 1 \end{bmatrix}\), B = \(\begin{bmatrix} 2 & 3\\ -1 & 0 \end{bmatrix}\). Find A2 + AB + B2.

Answers:

 

1. (i) \(\begin{bmatrix} 4 & -4\\ 4 & -4 \end{bmatrix}\)

(ii) \(\begin{bmatrix} 15 & 10\\ 24 & 17 \end{bmatrix}\)


2. (i) False

(ii) False


4. (ii) \(\begin{bmatrix} 4 & 9\\ 5 & 4 \end{bmatrix}\)

5. \(\begin{bmatrix} 3 & -1\\ 1 & -2 \end{bmatrix}\)

6. (i) x = -8, y = 2

(ii) x = 2, y = -8


7. x = 3, y = -4

8. x = \(\frac{3}{58}\), y = \(\frac{7}{29}\)

9. x = 3, y = 0

10. x = 3, y = -10

11. x = \(\frac{3}{4}\), y = \(\frac{5}{6}\), z = 5

12. x = 36

13. a = -6, b = -1

14. x = 1, y = 2

15. \(\begin{bmatrix} 1 & \frac{4}{3}\\ 4 & \frac{11}{3} \end{bmatrix}\)

16. \(\begin{bmatrix} \frac{1}{5}\\ \frac{2}{5} \end{bmatrix}\)

17. \(\begin{bmatrix} \frac{4}{5} & -\frac{1}{5}\\ -\frac{3}{5} & \frac{2}{5} \end{bmatrix}\)

18. \(\begin{bmatrix} -7 & 5\\ 6 & 2 \end{bmatrix}\)

19. \(\begin{bmatrix} 4 & 1\\ 1 & -6 \end{bmatrix}\).

20. (ii) \(\begin{bmatrix} 4 & 9\\ 5 & 4 \end{bmatrix}\).





10th Grade Math

From Worksheet on Matrix to HOME PAGE




Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.



Share this page: What’s this?

Recent Articles

RSS

  1. What are Parallel Lines in Geometry? | Two Parallel Lines | Examples

    Apr 19, 24 04:39 PM

    Examples of Parallel Lines
    In parallel lines when two lines do not intersect each other at any point even if they are extended to infinity. What are parallel lines in geometry? Two lines which do not intersect each other

    Read More

  2. Perpendicular Lines | What are Perpendicular Lines in Geometry?|Symbol

    Apr 19, 24 04:01 PM

    Perpendicular Lines
    In perpendicular lines when two intersecting lines a and b are said to be perpendicular to each other if one of the angles formed by them is a right angle. In other words, Set Square Set Square If two…

    Read More

  3. Fundamental Geometrical Concepts | Point | Line | Properties of Lines

    Apr 19, 24 01:50 PM

    Point P
    The fundamental geometrical concepts depend on three basic concepts — point, line and plane. The terms cannot be precisely defined. However, the meanings of these terms are explained through examples.

    Read More

  4. What is a Polygon? | Simple Closed Curve | Triangle | Quadrilateral

    Apr 19, 24 01:22 PM

    Square - Polygon
    What is a polygon? A simple closed curve made of three or more line-segments is called a polygon. A polygon has at least three line-segments.

    Read More

  5. Simple Closed Curves | Types of Closed Curves | Collection of Curves

    Apr 18, 24 01:36 AM

    Closed Curves Examples
    In simple closed curves the shapes are closed by line-segments or by a curved line. Triangle, quadrilateral, circle, etc., are examples of closed curves.

    Read More