Volume of Cuboid

Here we will learn how to solve the application problems on Volume of cuboid using the formula.

Formula for finding the volume of a cuboid

Volume of a Cuboid (V) = l × b × h;

Where l = Length, b = breadth and h = height.

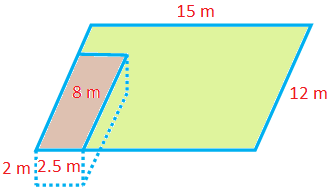
1. A field is 15 m long and 12 m broad. At one corner of this field a rectangular well of dimensions 8 m × 2.5 m × 2 m is dug, and the dug-out soil is spread evenly over the rest of the field. Find the rise in the level of the rest of the field.

Solution:

The volume of soil removed = the volume of the well

                                         = 8 m × 2.5 m × 2 m

                                         = 8 × 2.5 × 2 m³

                                         = 40 m³

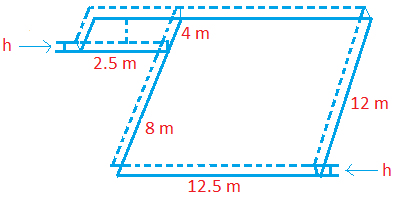
Let the level of the rest of the field be raised by h.

The volume of the soil spread evenly on the field

                            = volume of the cuboid of dimensions + volume of the cuboid of dimensions

                            = 2.5 m × 4 m × h + 12.5 m × 12 m × h

                            = (2.5 m × 4 m × h + 12.5 m × 12 m × h)

                            = (10h + 150h) m\(^{2}\)

                            = 160h m\(^{2}\)

Therefore, 160h m\(^{2}\) = 40 m³

⟹ h = \(\frac{40}{160}\) m

⟹ h = \(\frac{1}{4}\) m

Therefore, the rise in the level = \(\frac{1}{4}\) m

                                            = 25 cm

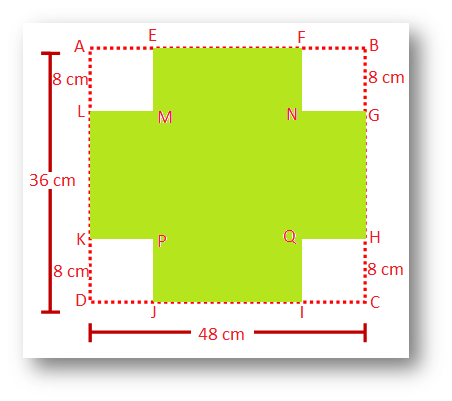
2. Squares each side 8 cm are cut off from the four corners of a sheet of tin measuring 48 cm by 36 cm. The remaining portion of the sheet is folded to form a tank open at the top. What will be the capacity of the tank?

Solution:

To make the tank, NGHP has to folded up along NP, LMQK along MQ, EFNM along MN and IJQP.

Now, MN = QP = (48 - 2 × 8) cm = 32 cm, and

NP = MQ = (36 - 2 × 8) cm = 20 cm.

EM = KQ = IP = GN = 8 cm.

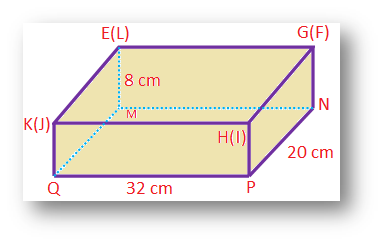
Therefore, the capacity of the tank = 32 × 20 × 8 cm³

= 5120 cm³

= 5.12 litres [Since, 1 litre = 1000 cm³]

9th Grade Math

From Volume of Cuboid to HOME PAGE