Vertex of the Hyperbola

We will discuss about the vertex of the hyperbola along with the examples.

Definition of the vertex of the hyperbola:

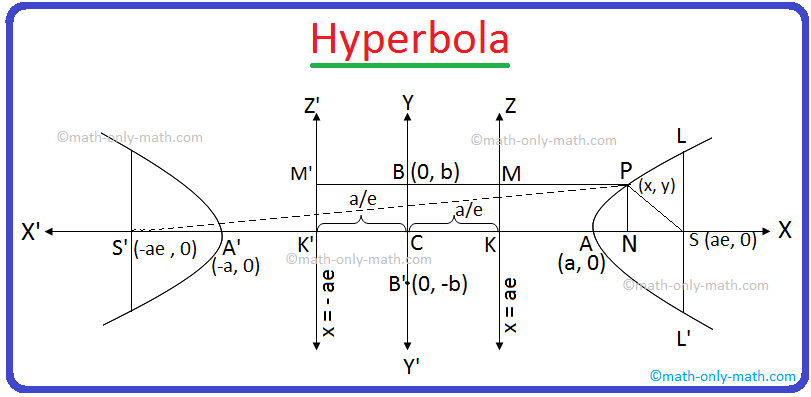
The vertex is the point of intersection of the line perpendicular to the directrix which passes through the focus cuts the hyperbola.

Suppose the equation of the hyperbola be $\frac{x^{2}}{a^{2}}$ - $\frac{y^{2}}{b^{2}}$ = 1 then, from the above figure we observe that the line perpendicular to the directrix KZ and passing through the focus S cuts the hyperbola at A and A'.

The points A and A', where the hyperbola meets the line joining the foci S and S' are called the vertices of the hyperbola.

Therefore, the hyperbola has two vertices A and A' whose co-ordinates are (a, 0) and (- a, 0) respectively.

Solved examples to find the vertex of a hyperbola:

1. Find the coordinates of the vertices of the hyperbola 9x$^{2}$ - 16y$^{2}$ - 144 = 0.

Solution:

The given equation of the hyperbola is 9x$^{2}$ - 16y$^{2}$ - 144 = 0

Now form the above equation we get,

9x$^{2}$ - 16y$^{2}$ = 144

Dividing both sides by 144, we get

$\frac{x^{2}}{16}$ - $\frac{y^{2}}{9}$ = 1

This is the form of $\frac{x^{2}}{a^{2}}$ - $\frac{y^{2}}{b^{2}}$ = 1, (a$^{2}$ > b$^{2}$), where a$^{2}$ = 16 or a = 4 and b$^{2}$ = 9 or b = 3

We know the coordinates of the vertices are (a, 0) and (-a, 0).

Therefore, the coordinates of the vertices of the hyperbola 9x$^{2}$ - 16y$^{2}$ - 144 = 0 are (4, 0) and (-4, 0).

2. Find the coordinates of the vertices of the hyperbola 9x$^{2}$ - 25y$^{2}$ - 225 = 0.

Solution:

The given equation of the hyperbola is 9x$^{2}$ - 25y$^{2}$ - 225 = 0

Now form the above equation we get,

9x$^{2}$ - 25y$^{2}$ = 225

Dividing both sides by 225, we get

$\frac{x^{2}}{25}$ - $\frac{y^{2}}{9}$ = 1

Comparing the equation $\frac{x^{2}}{25}$ - $\frac{y^{2}}{9}$ = 1 with the standard equation of hyperbola $\frac{x^{2}}{a^{2}}$ - $\frac{y^{2}}{b^{2}}$ = 1 (a$^{2}$ > b$^{2}$) we get,

a$^{2}$ = 25 or a = 5 and b$^{2}$ = 9 or b = 3

We know the coordinates of the vertices are (a, 0) and (-a, 0).

● The Hyperbola

• Definition of Hyperbola
• Standard Equation of an Hyperbola
  
• Vertex of the Hyperbola
• Centre of the Hyperbola
• Transverse and Conjugate Axis of the Hyperbola
• Two Foci and Two Directrices of the Hyperbola
• Latus Rectum of the Hyperbola
• Position of a Point with Respect to the Hyperbola
• Conjugate Hyperbola
• Rectangular Hyperbola
• Parametric Equation of the Hyperbola
• Hyperbola Formulae
• Problems on Hyperbola

11 and 12 Grade Math 

From Vertex of the Hyperbola to HOME PAGE