Two-point Form of a Line
We will discuss here about the method of finding the equation of a straight line in the two point form.
To find the equation of a straight line in the two point form,
Let AB be a line passing through two points A (x1, y1) and B (x2, y2).
Let the equation of the line be y = mx + c ................... (i), where m is the slope of the line and c is the y-intercept.
As (x1, y1) and (x2, y2) are points on the line AB, (x1, y1) and (x2, y2) satisfy (i).
Therefore, y1 = mx1 + c ................................ (ii)
and y2 = mx2 + c ................................ (iii)
Subtracting (iii) from (ii),
y1 - y2 = m(x1 - x2)
⟹ m = y1−y2x1−x2 ................................ (iv)
Substituting m = y1−y2x1−x2 in (ii),
y1 = [y1−y2x1−x2]x1 + c
⟹ c = y1 - x1(y1−y2)x1−x2
⟹ c = y1(x1−x2)−x1(y1−y2)x1−x2
⟹ c = x1y2−x2y1x1−x2
Therefore, from (i),
y = [y1−y2x1−x2]x + x1y2−x2y1x1−x2
Subtracting y1 from both sides of (v)
y - y1 = [y1−y2x1−x2]x + x1y2−x2y1x1−x2
⟹ y - y1 = [y1−y2x1−x2]x + x1(y2−y1)x1−x2
⟹ y - y1 = y1−y2x1−x2(x + x1)
The equation of the straight line passing through (x1, y1) and (x2, y2) is y - y1 = y1−y2x1−x2(x + x1)
Note: From (iv), the slope of the line joining the points (x1, y1) and (x2, y2) is y1−y2x1−x2 i.e., Differenceofy−coordinatesdifferenceofx−coordinatesinthesameorder
Solved example on two-point form of a line:
The equation of the line passing through the points (1, 1) and (-3, 2) is
y - 1 = 1−21−(−3)(x - 1)
⟹ y – 1 = -14(x – 1)
Also, y – 2 = 2−1−3−1(x + 3)
⟹ y – 2 = -14(x + 3)
However, the two equations are the same.
● Equation of a Straight Line
- Inclination of a Line
- Slope of a Line
- Intercepts Made by a Straight Line on Axes
- Slope of the Line Joining Two Points
- Equation of a Straight Line
- Point-slope Form of a Line
- Two-point Form of a Line
- Equally Inclined Lines
- Slope and Y-intercept of a Line
- Condition of Perpendicularity of Two Straight Lines
- Condition of parallelism
- Problems on Condition of Perpendicularity
- Worksheet on Slope and Intercepts
- Worksheet on Slope Intercept Form
- Worksheet on Two-point Form
- Worksheet on Point-slope Form
- Worksheet on Collinearity of 3 Points
- Worksheet on Equation of a Straight Line
From Point-slope Form of a Line to HOME
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
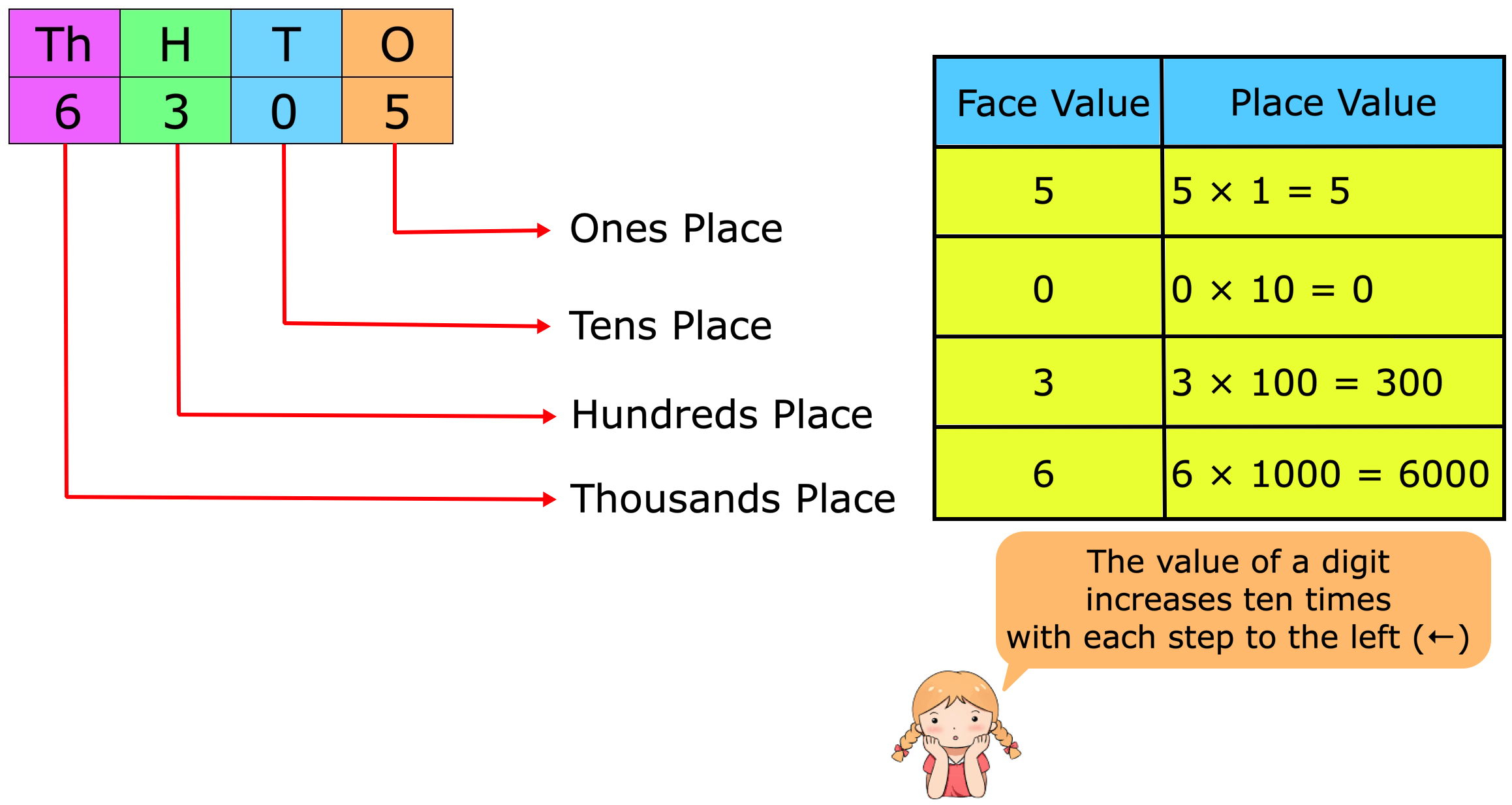
Place Value and Face Value | Place and Face Value of Larger Number
Apr 13, 25 03:12 PM
The place value of a digit in a number is the value it holds to be at the place in the number. We know about the place value and face value of a digit and we will learn about it in details. We know th… -
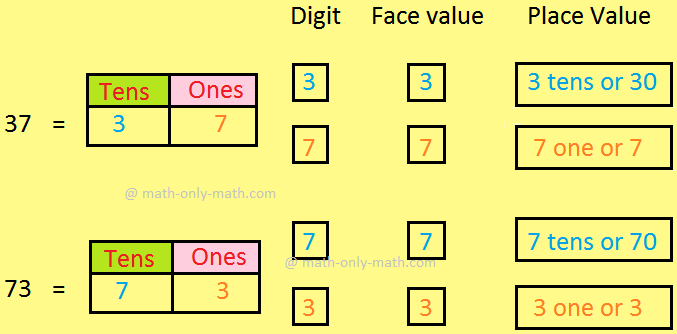
Face Value and Place Value|Difference Between Place Value & Face Value
Apr 13, 25 03:07 PM
What is the difference between face value and place value of digits? Before we proceed to face value and place value let us recall the expanded form of a number. The face value of a digit is the digit… -
Place Value and Face Value | Basic Concept on Place Value | Face Value
Apr 13, 25 02:59 PM
Learn the easiest way to understand the basic concept on place value and face value in the second grade. Suppose we write a number in figures 435 in words we write four hundred thirty five. -
Expressing Place Value and Face Value | International & Indian System
Apr 13, 25 02:35 PM
We will learn expressing place value and face value of a digit in any number in International and Indian system. Place value: We know how to find out the place value of a digit in any number. -
5th Grade Decimals | Word Problem on Decimals | Concept of Decimals
Apr 13, 25 02:16 PM
A fractional number whose denominator is 10 or multiple of 10 is called a decimal. Every decimal has two parts whole number part and decimal part. These two parts are separated by a dot or point. This…



New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.