Trigonometrical Ratios of 60°

How to find the Trigonometrical Ratios of 60°?

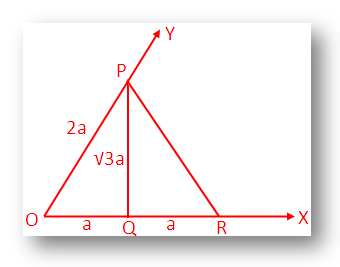
Let a rotating line $\overrightarrow{OX}$ rotates about O in the anti-clockwise sense and starting from its initial position $\overrightarrow{OX}$ traces out ∠XOY = 60° is shown in the above picture.

Take a point P on $\overrightarrow{OY}$ and draw $\overline{PQ}$ perpendicular to $\overrightarrow{OX}$.

Let a rotating line $\overrightarrow{OX}$ rotates about O in the anti-clockwise sense and starting from its initial position $\overrightarrow{OX}$ traces out ∠XOY = 60° is shown in the above picture.

Take a point P on $\overrightarrow{OY}$ and draw $\overline{PQ}$ perpendicular to $\overrightarrow{OX}$.

Now, take a point R on $\overrightarrow{OX}$ such that $\overline{OQ}$ = $\overline{QR}$  and join $\overline{PR}$.

From △OPQ and △PQR we get,

$\overline{OQ}$  = $\overline{QR}$,

$\overline{PQ}$ common

and ∠PQO = ∠PQR (both are right angles)

Thus, the triangles are congruent.

Therefore,  ∠PRO = ∠POQ = 60°

Therefore, ∠OPR

= 180°  - ∠POQ - ∠PRO

= 180°  - 60° - 60°

=  60°

Therefore, the △POR is equilateral triangle

Let, OP = OR = 2a;

Thus, OQ = a.

Now, from pythagoras theorem we get,

OQ² + PQ² = OP²

⇒ a² + PQ² = (2a)²

⇒ PQ² = 4a² – a²

⇒ PQ² = 3a²

Taking square roots on both the sides we get,

PQ = √3a (since, PQ > 0)

Therefore, from the right angled triangle POQ we get,
sin 60° = $\frac{\overline{PQ}}{\overline{OP}} = \frac{\sqrt{3} a}{2a} = \frac{\sqrt{3}}{2}$;
cos 60° = $\frac{\overline{OQ}}{\overline{OP}} = \frac{a}{2a} = \frac{1}{2}$
And tan 60° = $\frac{\overline{PQ}}{\overline{OQ}} = \frac{\sqrt{3} a}{a} = \sqrt{3}$
Therefore, csc 60° = $\frac{1}{sin  60°} = \frac{2}{\sqrt{3}} = \frac{2 \sqrt{3}}{3}$
sec 60° = $\frac{1}{cos  60°}$= 2
And cot 60° =  $\frac{1}{tan  60°} = \frac{1}{\sqrt{3}} = \frac{ \sqrt{3}}{3}$

Trigonometrical Ratios of 60° are commonly called standard angles and the trigonometrical ratios of these angles are frequently used to solve particular angles.

● Trigonometric Functions

• Basic Trigonometric Ratios and Their Names
• Restrictions of Trigonometrical Ratios
• Reciprocal Relations of Trigonometric Ratios
• Quotient Relations of Trigonometric Ratios
  
• Limit of Trigonometric Ratios
  
• Trigonometrical Identity
• Problems on Trigonometric Identities
• Elimination of Trigonometric Ratios
• Eliminate Theta between the equations
• Problems on Eliminate Theta
• Trig Ratio Problems
• Proving Trigonometric Ratios
• Trig Ratios Proving Problems
• Verify Trigonometric Identities
• Trigonometrical Ratios of 0°
• Trigonometrical Ratios of 30°
• Trigonometrical Ratios of 45°
• Trigonometrical Ratios of 60°
• Trigonometrical Ratios of 90°
• Trigonometrical Ratios Table
• Problems on Trigonometric Ratio of Standard Angle
  
• Trigonometrical Ratios of Complementary Angles
• Rules of Trigonometric Signs
• Signs of Trigonometrical Ratios
  
• All Sin Tan Cos Rule
• Trigonometrical Ratios of (- θ)
• Trigonometrical Ratios of (90° + θ)
• Trigonometrical Ratios of (90° - θ)
• Trigonometrical Ratios of (180° + θ)
• Trigonometrical Ratios of (180° - θ)
• Trigonometrical Ratios of (270° + θ)
• Trigonometrical Ratios of (270° - θ)
• Trigonometrical Ratios of (360° + θ)
• Trigonometrical Ratios of (360° - θ)
• Trigonometrical Ratios of any Angle
• Trigonometrical Ratios of some Particular Angles
• Trigonometric Ratios of an Angle
• Trigonometric Functions of any Angles
• Problems on Trigonometric Ratios of an Angle
• Problems on Signs of Trigonometrical Ratios

11 and 12 Grade Math

From Trigonometrical Ratios of 60° to HOME PAGE